In der Pharmakologie wird das in positive \(x\)-Richtung unbegrenzte Flächenstück, das sich im I. Quadranten zwischen \(G_{f}\) und der \(x\)-Achse befindet, als AUC (area under the curve") bezeichnet. Nur dann, wenn diesem Flächenstück ein endlicher Flächeninhalt zugeordnet werden kann, kann die betrachtete Funktion \(f\) die zeitliche Entwicklung der Wirkstoffkonzentration auch für große Zeitwerte \(x\) realistisch beschreiben.
Die \(x\)-Achse, \(G_{f}\) und die Gerade mit der Gleichung \(x = b\) mit \(b \in \mathbb R^{+}\) schließen im I. Quadranten ein Flächenstück mit dem Inhalt \(A(b)\) ein. Bestimmen Sie mithilfe der in Aufgabe d angegebenen Stammfunktion \(F\) einen Term für \(A(b)\) und beurteilen Sie unter Verwendung dieses Terms, ob die Funktion \(f\) auch für große Zeitwerte eine realistische Modellierung der zeitlichen Entwicklung der Wirkstoffkonzentration darstellt.
(4 BE)
Lösung zu Teilaufgabe g
\(F(x) = 4 \cdot \ln{(x + 1)} + \dfrac{4}{x + 1}; \; D_{F} = \; ]-1;+\infty[\) (vgl. Teilaufgabe d)
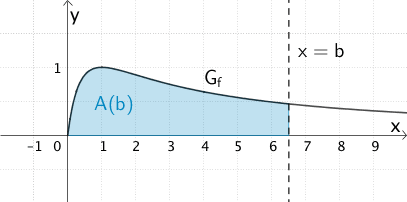
Flächenstück mit dem Flächeninhalt \(A(b)\), welches die \(x\)-Achse, \(G_{f}\) und die Gerade mit der Gleichung \(x = b\) mit \(b \in \mathbb R^{+}\) im I. Quadranten einschließen.
Bestimmung eines Terms für \(A(b)\)
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*} A(b) &= \int_{0}^{b} f(x) dx \\[0.8em] &= [F(x)]_{0}^{b} \\[0.8em] &= \left[ 4 \cdot \ln{(x + 1)} + \frac{4}{x + 1} \right]_{0}^{b} \\[0.8em] &= 4 \cdot \ln{(x + b)} + \frac{4}{b + 1} - \left( 4 \cdot \ln{(0 + 1)} + \frac{4}{0 + 1} \right) \\[0.8em] &= 4\ln{(b + 1)} + \frac{4}{b + 1} - 4\underbrace{\ln{1}}_{0} - 4 \\[0.8em] &= 4\ln{(b + 1)} + \frac{4}{b + 1} - 4 \end{align*}\]
Beurteilung anhand des Terms von \(A(b)\)
\[\lim \limits_{b\,\to\,+\infty} A(b) = \lim \limits_{b\,\to\,+\infty} \Big( 4\underbrace{\ln{(b + 1)}}_{\to\,+\infty} + \underbrace{\frac{4}{b + 1}}_{\to\,0} - 4 \Big) = +\infty\]
Da der Flächeninhalt \(A(b)\) einen unendlich großen Wert annehmen kann, eignet sich die Funktion \(f\) für große Zeitwerte \((b \to +\infty)\) nicht als realistische Modellierung der zeitlichen Entwicklung der Wirkstoffkonzentration.


