Abiturlösungen Mathematik Bayern Beispiel-Abiturprüfung 2014 Prüfungsteil B Analysis 2
Abiturlösungen Mathematik Bayern Beispiel-Abiturprüfung 2014 Prüfungsteil B Analysis 2
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f\,\colon x \mapsto 3 \cdot \left(1 - e^{-x}\right) - x\). Der Graph von \(f\) wird mit \(G_f\) bezeichnet.
Bestimmen Sie das Verhalten von \(f\) an den Grenzen der Definitionsmenge.
(2 BE)
- Details
- Hauptkategorie: Prüfungsteil B
Zeigen Sie, dass \(G_f\) genau einen Hochpunkt besitzt, und geben Sie dessen Koordinaten an.
(zur Kontrolle: \(x\)-Koordinate des Hochpunkts: \(\ln 3\))
(5 BE)
- Details
- Hauptkategorie: Prüfungsteil B
Berechnen Sie \(f(0)\) sowie \(f(3)\) und skizzieren Sie \(G_f\) unter Berücksichtigung der bisherigen Ergebnisse in einem Koordinatensystem.
(3 BE)
- Details
- Hauptkategorie: Prüfungsteil B
Im Intervall \([2;3]\) besitzt \(f\) genau eine Nullstelle \(a\). Bestimmen Sie einen Näherungswert von \(a\), indem Sie den ersten Schritt des Newton-Verfahrens mit dem Startwert 3 durchführen. Man erhält dadurch \(a\) auf zwei Dezimalen genau.
(Ergebnis: \(a \approx 2{,}82\))
(3 BE)
- Details
- Hauptkategorie: Prüfungsteil B
Berechnen Sie durch Integration mithilfe des Näherungswerts von \(a\) einen Näherungswert für den Inhalt des Flächenstücks, das \(G_f\) im ersten Quadranten mit der \(x\)-Achse einschließt.
(5 BE)
- Details
- Hauptkategorie: Prüfungsteil B
Betrachtet wird nun die in \(\mathbb R\) definierte Funktion \(\displaystyle F\,\colon\,x\mapsto \int_{a}^{x}f(t)\,dt\).
Geben Sie an, welche besonderen Eigenschaften der Graph von \(F\) im Punkt \((a|F(a))\) hat; begründen Sie jeweils Ihre Antwort.
(4 BE)
- Details
- Hauptkategorie: Prüfungsteil B
Geben Sie den Zusammenhang zwischen der Funktion \(F\) und dem Ergebnis der Aufgabe 1e an.
(1 BE)
- Details
- Hauptkategorie: Prüfungsteil B
Jeder Körper sendet elektromagnetische Strahlung unterschiedlicher Frequenzen aus; die Intensität der Strahlung hängt von der Frequenz der Strahlung ab. Im Idealfall lässt sich diese Intensität nach Max Planck durch die Schar der in \(\mathbb R^+\) definierten Funktionen
\[I_T\,\colon x \mapsto \frac{x^3}{e^{\frac{x}{T}} - 1}\]
mit \(T \in \mathbb R^+\) beschreiben. Dabei ist \(x\) - bis auf eine Konstante - die Frequenz der Strahlung und \(T\) die Temperatur des Körpers in Kelvin.
Die Abbildung zeigt die zu drei Werten des Parameters \(T\) gehörenden Graphen von \(I_T\).
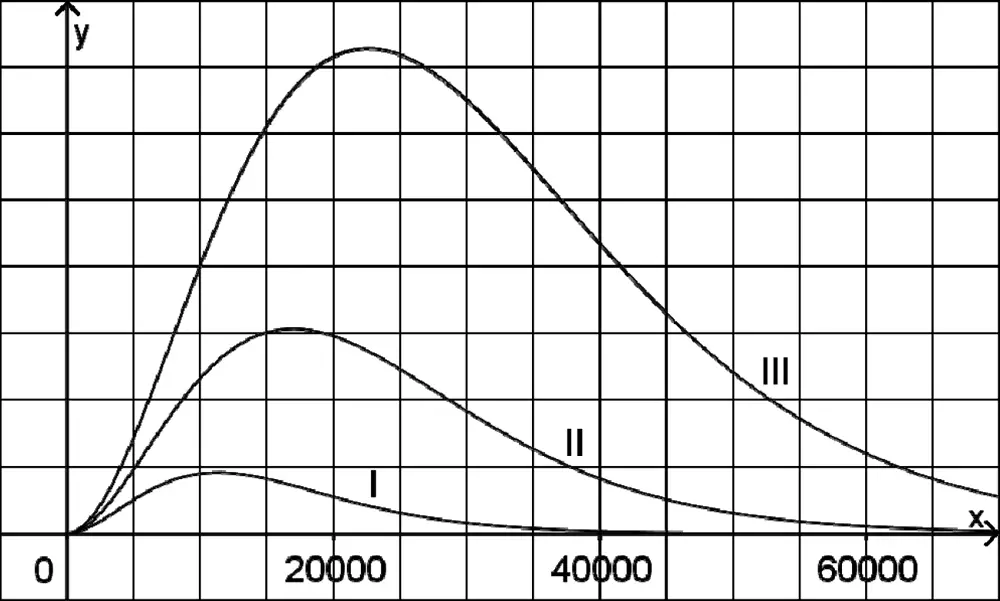
Bei der Bearbeitung der folgenden Aufgaben soll auf die Verwendung von Einheiten verzichtet werden.
Weisen Sie anhand des Funktionsterms von \(I_T\) nach, dass der Wert der Intensität der Strahlung stets positiv ist.
(3 BE)
- Details
- Hauptkategorie: Prüfungsteil B
Zeigen Sie, dass für die erste Ableitung der Funktion \(I_T\) gilt:
\[I'_T(x) = \frac{x^2 \cdot e^{\frac{x}{T}} \cdot \left [ 3 \cdot \left (1 - e^{-\frac{x}{T}} \right ) - \frac{x}{T} \right ]}{\left ( e^{\frac{x}{T}} - 1 \right )^2}\]
Vergleichen Sie diesen Term mit dem der Funktion \(f\) aus Aufgabe 1 und begründen Sie, dass die Funktion \(I_T\) bei \(x = a \cdot T\) ihr einziges Maximum besitzt, wenn \(a\) die positive Nullstelle von \(f\) ist.
(6 BE)
- Details
- Hauptkategorie: Prüfungsteil B
Das Maximum der Intensität der Strahlung unserer Sonne liegt bei \(x_{\text{max}} = 17 \cdot 10^3\). Bestimmen Sie damit einen Näherungswert für die Oberflächentemperatur der Sonne.
(2 BE)
- Details
- Hauptkategorie: Prüfungsteil B
Jeder der in der Abbildung dargestellten Graphen I, II und III gehört zu genau einer der Temperaturen 4000 K, 6000 K und 8000 K. Ordnen Sie die Temperaturen den Graphen zu und begründen Sie Ihre Zuordnung.
(3 BE)
- Details
- Hauptkategorie: Prüfungsteil B
Wird die Temperatur \(T\) eines Körpers verdoppelt, so nimmt das Maximum der Intensität seiner Strahlung den achtfachen Wert an. Begründen Sie diese Tatsache.
(3 BE)
- Details
- Hauptkategorie: Prüfungsteil B
2023 Christian Rieger・mathelike
