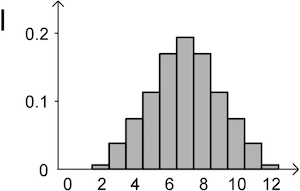
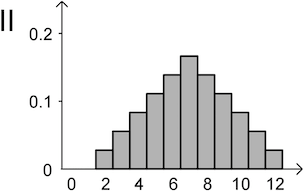
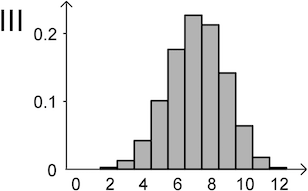
Die Wahrscheinlichkeitsverteilungen von \(X\) und \(Y\) werden jeweils durch eines der folgenden Diagramme I, II und III dargestellt. Ordnen Sie \(X\) und \(Y\) jeweils dem passenden Diagramm zu und begründen Sie Ihre Zuordnung.
(3 BE)
Lösung zu Teilaufgabe b
Zuordnung der Wahrscheinlichkeitsverteilung von \(X\)
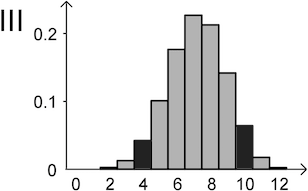
Da \(\boldsymbol{P(X = 4) = P(X = 10)}\) gilt (vgl. Teilaufgabe a) kann Diagramm III nicht die Wahrscheinlichkeitverteilung von \(X\) darstellen.
Um die Wahrscheinlichkeitsverteilung von \(X\) einem der Diagramme I oder II zuzuordnen, werden Wahrscheinlichkeiten für bestimmte Werte verglichen, beispielsweise wie folgt:
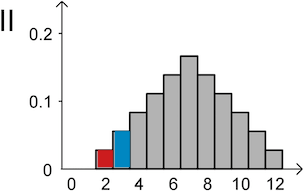
\[\textcolor{#0087c1}{\text{„Augensumme ist drei"}} = \{\textcolor{#0087c1}{(1;2)}, \textcolor{#0087c1}{(2;1)}\}\]
\[\textcolor{#cc071e}{\text{„Augensumme ist zwei"}} = \{\textcolor{#cc071e}{(1;1)}\}\]
Damit ist die Wahrscheinlichkeit \(P(\textcolor{#0087c1}{X = 3}) = \dfrac{\textcolor{#0087c1}{2}}{36}\) doppelt so groß wie die Wahrscheinlichkeit \(P(\textcolor{#cc071e}{X = 2}) = \dfrac{\textcolor{#cc071e}{1}}{36}\) (vgl. Teilaufgabe a).
Folglich stellt Diagramm II die Wahrscheinlichkeitsverteilung von \(X\) dar.
oder
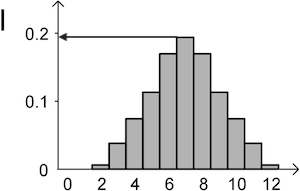
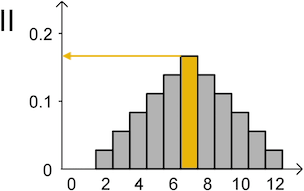
Diagramm I zeigt für den Wert \(7\) eine Wahrscheinlichkeit von ungefähr \(0{,}2\), Diagramm II zeigt eine deutlich kleinere Wahrscheinlichkeit.
\(\textcolor{#e9b509}{\text{„Augensumme ist sieben"}} = \{\textcolor{#e9b509}{(1;6)}, \textcolor{#e9b509}{(2;5)}, \textcolor{#e9b509}{(3;4)}, \textcolor{#e9b509}{(4;3)}, \textcolor{#e9b509}{(5;2)}, \textcolor{#e9b509}{(6;1)}\}\)
\(P(\textcolor{#e9b509}{X = 7}) = \dfrac{\textcolor{#e9b509}{6}}{36} = \textcolor{#e9b509}{\dfrac{1}{6}}\) (vgl. Teilaufgabe a)
\[\textcolor{#e9b509}{\dfrac{1}{6}} < \frac{1}{5} = 0{,}2\]
Somit stellt Diagramm II die Wahrescheinlichkeitsverteilung von \(X\) dar.
oder
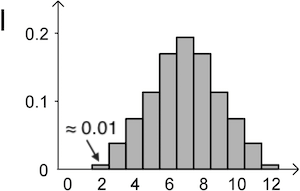
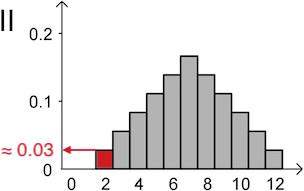
Diagramm I zeigt für den Wert \(2\) eine Wahrscheinlichkeit von ungefähr \(0{,}01\), Diagramm II zeigt eine Wahrscheinlichkeit von ungefähr \(\textcolor{#cc071e}{0{,}03}\).
\[\textcolor{#cc071e}{\text{„Augensumme ist zwei"}} = \{\textcolor{#cc071e}{(1;1)}\}\]
\(P(\textcolor{#cc071e}{X = 2}) = \dfrac{\textcolor{#cc071e}{1}}{36} \approx \dfrac{3}{100} = \textcolor{#cc071e}{0{,}03}\) (vgl. Teilaufgabe a)
Somit stellt Diagramm II die Wahrscheinlichkeitsverteilung von \(X\) dar.
Zuordnung der Wahrscheinlichkeitsverteilung von \(Y\)

Die Zufallsgröße \(Y\) ist mit einer konstanten Trefferwahrscheinlichkeit von \(p = 0{,}6\) für das Ziehen mit Zurücklegen einer schwarzen Kugel und einer Länge der Bernoullikette von \(n = 12\) (12-maliges Ziehen) nach \(B(0{,}6;12)\) binomialverteilt (vgl. Angabe Stochastik 1 Prüfungsteil A).
Binomialverteilte Zufallsgröße
Für eine Zufallsgröße \(X\), welche bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0,1,\dots,n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, gilt:
Binomialverteilung (vgl. Merkhilfe)
\[P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \quad (0 \leq k \leq n)\]
Eine Binomialverteilung ist durch die Parameter \(n\) und \(p\) eindeutig bestimmt und wird durch das Symbol \(B(n:p)\) gekennzeichnet. \(X\) heißt binomialverteilt nach \(B(n;p)\).
Voraussetzung für eine Binomialverteilung
Ein Zufallsexperiment, bei dem nur zwei sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können (Bernoulli-Experiment).
Da eine Binomialverteilung nur für \(p = 0{,}5\) symmetrisch ist, können die Diagramme I und II nicht die Wahrscheinlichkeitsverteilung von \(Y\) darstellen (vgl. Abiturskript - 3.3.3 Binomialverteilte Zufallsgröße).
Für die asymmetrische Wahrscheinlichkeitsverteilung von \(Y\) kommt nur Diagramm III in Frage.


