Abbildung 1 zeigt den Graphen \(G_f\) einer in \(]-\infty;5[\) definierten Funktion \(f\,\).
Skizzieren Sie in der Abbildung den Graphen der zugehörigen Ableitungsfunktion \(f'\,\). Berücksichtigen Sie dabei insbesondere einen Näherungswert für \(f'(0)\), die Nullstelle von \(f'\) und das Verhalten von \(f'\) für \(x \mapsto 5\,\).
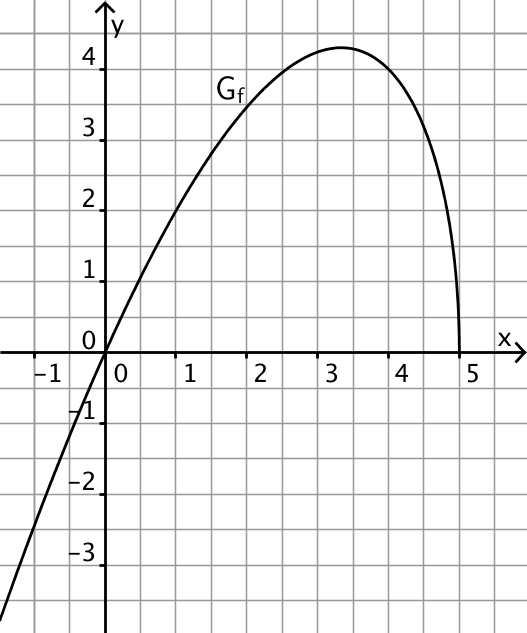Abb. 1
(4 BE)
Lösung zu Teilaufgabe 4
Näherungswert für \(f'(0)\)
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Die Steigung \(m_t\) der Tangente \(t\) an \(G_f\) an der Stelle \(x = 0\) liefert den Näherungswert für \(f'(0)\,\).
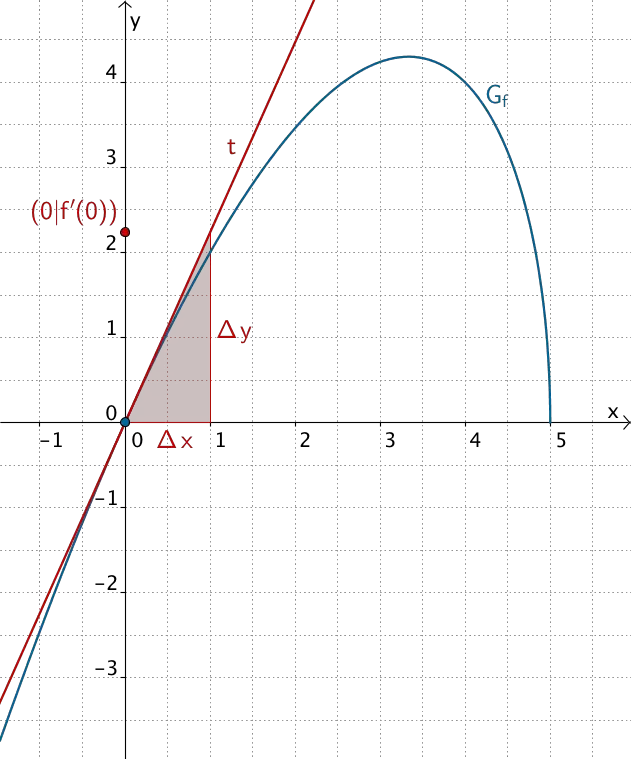
Tangente \(t\) an \(G_f\) an der Stelle \(x = 0\)
\[f'(0) = m_t = \frac{\Delta \, y}{\Delta \, x} \approx \frac{2{,}2}{1} = 2{,}2\]
Nullstelle von \(f'\)
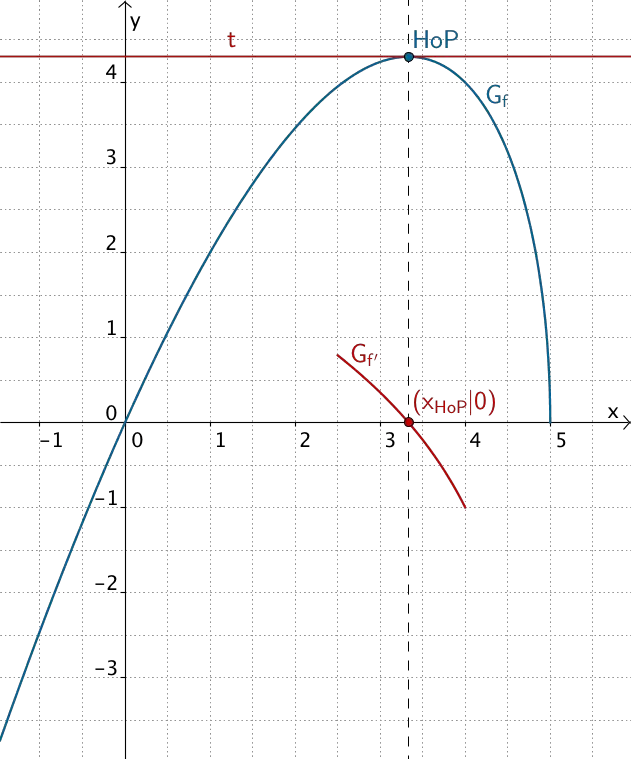
Hochpunkt \(\,HoP\,\) von \(\,G_f\,\), Nullpunkt \(\,(x_{HoP}|0)\,\) von \(\,G_{f'}\,\)
Der Graph von \(f\) besitzt an der Stelle \(x \approx 3{,}3\) einen Hochpunkt und somit eine waagrechte Tangente \(t\,\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[\Longrightarrow \quad f'(x_{HoP}) = m_t = 0\]
Verhalten von \(f'\) in der Umgebung der Nullstelle:
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\(f\,\) steigt streng monoton für \(\,x < x_{HoP}\) \(\quad \Longrightarrow \quad f'(x) > 0\,\) für \(\,x < x_{HoP}\)
\(f\,\) fällt streng monoton für \(\,x > x_{HoP}\) \(\, \enspace \quad \Longrightarrow \quad f'(x) < 0\,\) für \(\,x > x_{HoP}\)
Verhalten von \(f'\) für \(x \to 5\)
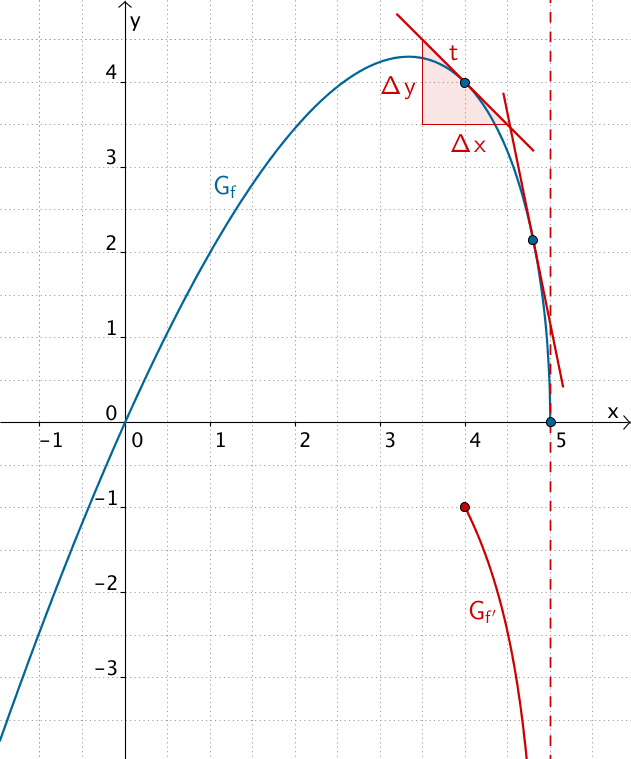
Tangenten \(\,t\,\) an \(\,G_f\,\) für \(\,x \to 5\)
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
An der Stelle \(x = 4\) lässt sich die Steigung \(m_t\) der Tangente \(t\) an den Graphen von \(f\) noch gut bestimmen.
\[f'(4) = m_t = \frac{\Delta\,y}{\Delta\,x} = \frac{-1}{1} = -1\]
Für \(x \to 5\) nimmt die Tangentensteigung \(m_t\) beliebig große negative Werte an, bis sie an der Stelle \(x = 5\) nicht mehr existiert. Der Graph von \(f\) steht im Punkt \((5|0)\) senkrecht zur \(x\)-Achse.
\[\lim \limits_{x\,\to\,5^-} f'(x) = -\infty\]
Der Graph der Ableitugsfunktion \(f'\) nähert sich von links der senkrechten Asymptote mit der Gleichung \(x = 5\) an.
Zusammenfassung der Ergebnisse, Skizzieren von \(G_{f'}\)
\[f'(0) \approx 2{,}2\]
\[f'(3{,}3) = 0\]
\[\lim \limits_{x\,\to\,5^-} f'(x) = -\infty\]
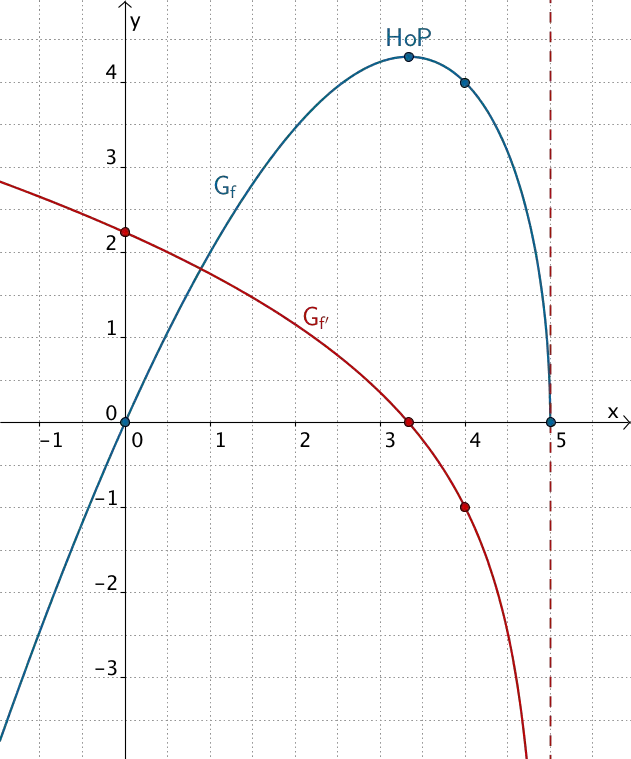
Graph der Funktion \(\,f\,\) und Graph der Ableitungsfunktion \(\,f'\,\)
