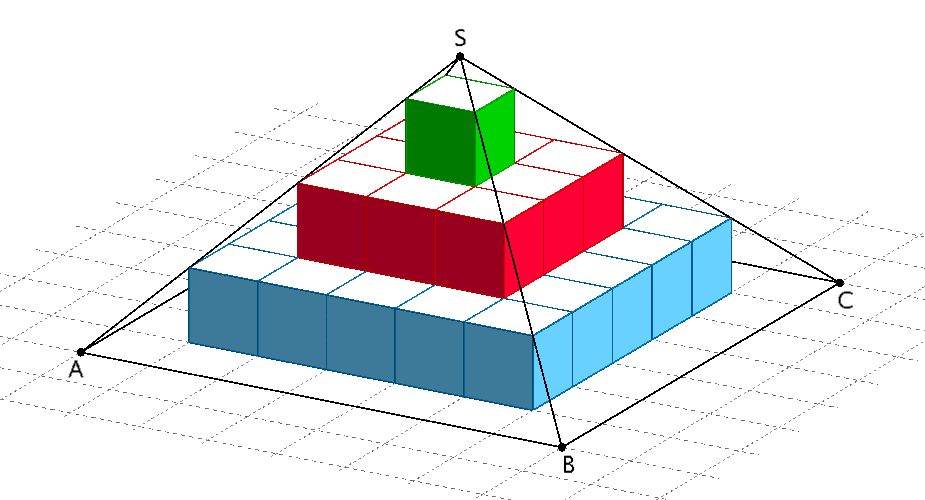
Die Abbildung zeigt die Pyramide \(ABCDS\) mit quadratischer Grundfläche \(ABCD\). Der Pyramide ist eine Stufenpyramide einbeschrieben, die aus Würfeln mit der Kantenlänge 1 besteht.
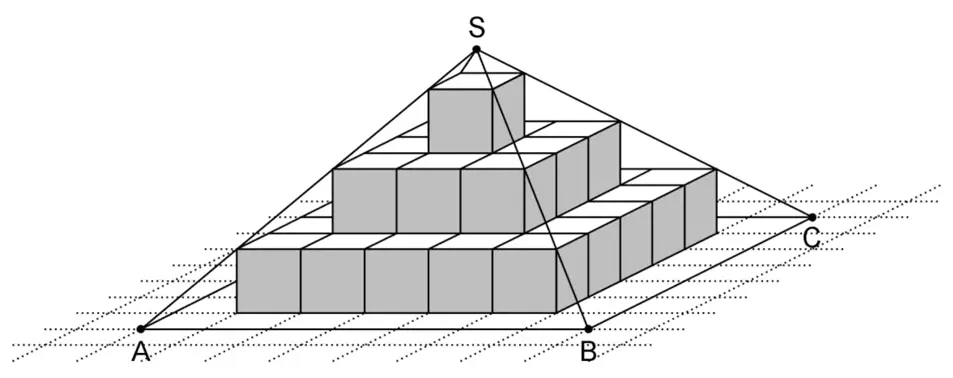
Geben Sie das Volumen der Stufenpyramide und die Höhe der Pyramide \(ABCDS\) an.
(2 BE)
Lösung zu Teilaufgabe 2a
Volumen eines Würfels/einer Stufenpyramide, Höhe einer Pyramide
Volumen der Stufenpyramide
Pyramide \(ABCDS\) mit einbeschriebener Stufenpyramide
Die einbeschrieben Stufenpyramide besteht aus \(5 \cdot 5 + 3 \cdot 3 + 1 = 35\) Würfeln mit der Kantenlänge 1, wobei der Volumeninhalt eines Würfels 1 VE (Volumeneinheit) beträgt.
\[\Longrightarrow \quad V_{\text{Stufenpyramide}} = 35 \cdot 1 \;\text{VE} = 35 \;\text{VE}\]
Höhe der Pyramide \(ABCDS\)
1. Möglichkeit
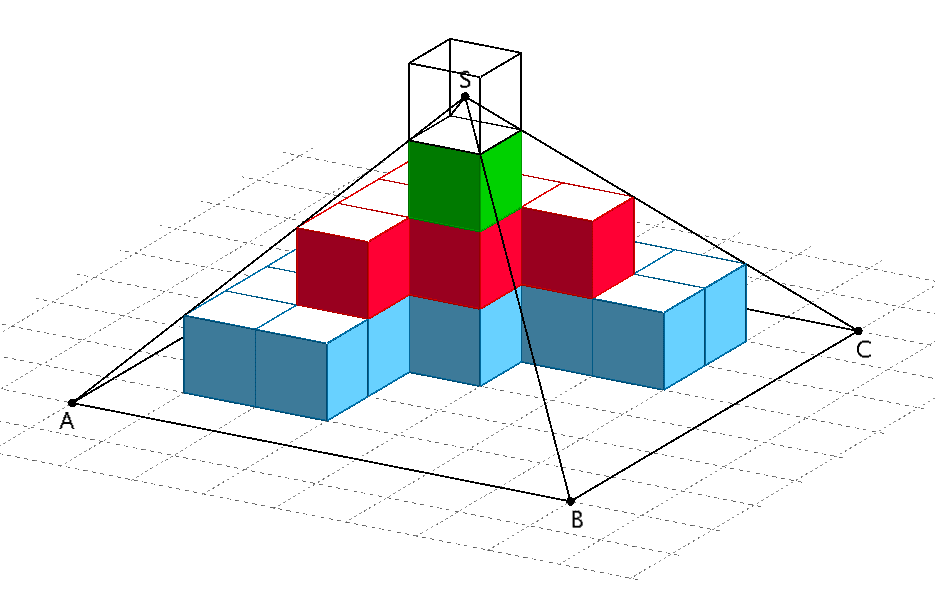
Denk man sich einen weiteren Würfel mit der Kantenlänge 1, der flächendeckend auf dem oberen Würfel (grün) der Stufenpyramide platziert ist, so ist die Pyramidenspitze \(S\) der Diagonalenschnittpunkt des gedachten Würfels. Der Punkt \(S\) liegt damit 0,5 LE (Längeneinheiten) über dem oberen Würfel der Stufenpyramide.
\[\Longrightarrow \quad h_{ABCDS} = (1 + 1+ 1+ 0{,}5) \;\text{LE} = 3{,}5 \;\text{LE}\]
2.Möglichkeit
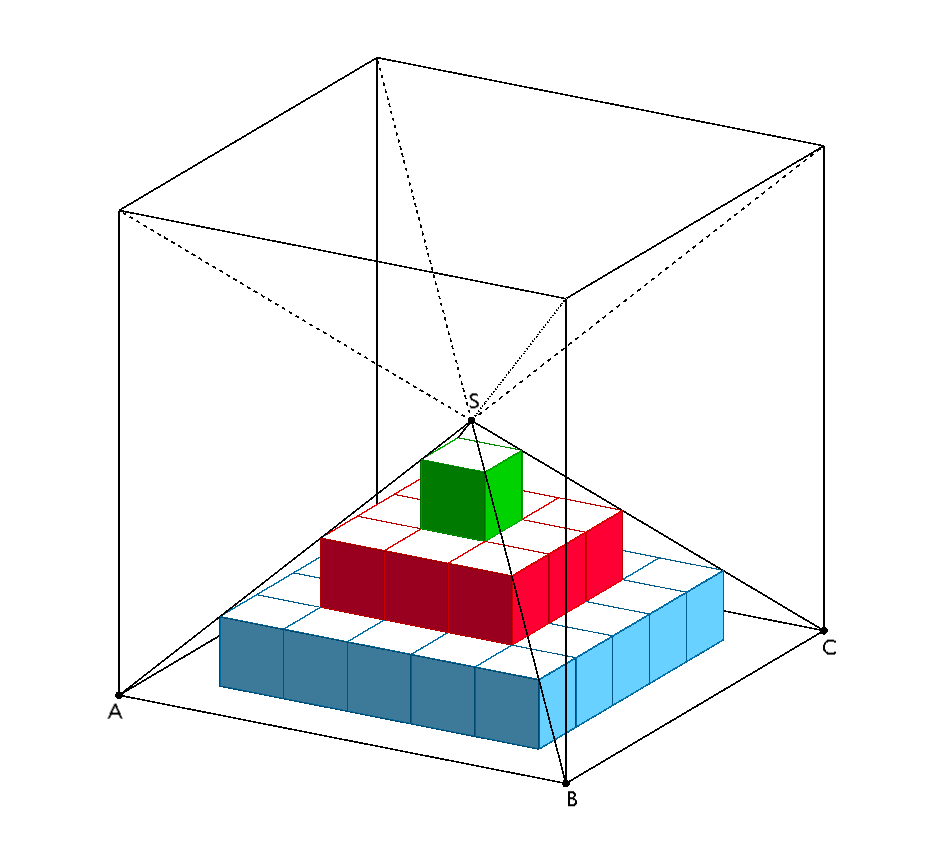
Denkt man sich einen Würfel über dem Quadrat \(ABCD\), so ist die Pyramidenspitze \(S\) der Diagonalenschnittpunkt des gedachten Würfels.
Aus der Abbildung zu Aufgabe 2 kann die Kantenlänge des gedachten Würfels zu \(\overline{AB} = \overline{BC} = 7\) entnommen werden. Damit beträgt der Abstand des Diagonalenschnittpunkts des Würfels vom Quadrat \(ABCD\) 3,5 LE (Längeneinheiten).
\[\Longrightarrow \quad h_{ABCDS} = 3{,}5\;\text{LE}\]