Die Punkte \(A(0|2|2)\), \(B(2|3|0)\) und \(C(0|-2|4)\) legen die Ebene \(E\) fest.
a) Ermitteln Sie eine Gleichung der Ebene \(E\) in Normalenform.
(mögliches Ergebnis: \(E \colon 3x_{1} + 2x_{2} + 4x_{3} = 12\))
b) Ermitteln Sie die Koordinaten der Schnittpunkte \(S_{1}\), \(S_{2}\) und \(S_{3}\) der Ebene \(E\) mit der \(x_{1}\)-, \(x_{2}\)- bzw. \(x_{3}\)-Achse und veranschaulichen Sie die Lage der Ebene \(E\) in einem kartesischen Koordinatensystem.
c) Bestimmen Sie eine Gleichung der Schnittgeraden \(s\) der Ebene \(E\) und der \(x_{2}x_{3}\)-Ebene.
d) Berechnen Sie die Koordinaten des Punktes \(S'\), der durch Spiegelung des Punktes \(S_{1}\) an der Geraden \(s\) hervorgeht.
a) Gleichung der Ebene \(E\) in Normalenform
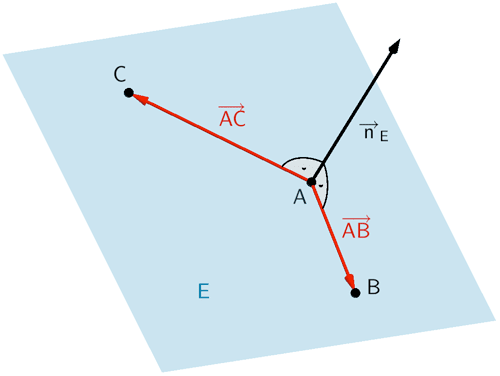
Das Vektorprodukt (Kreuzprodukt) zweier linear unabhängiger Vektoren, beispielsweise der Verbindungsvektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\), liefert einen Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\). Als Aufpunkt wählt man einen der gegebenen Punkte \(A\), \(B\) oder \(C\). Damit lässt sich eine Gleichung der Ebene in Normalenform angeben.
Der Ansatz kann mithilfe der Normalenform in Vektordarstellung oder in Koordinatendarstellung erfolgen (vgl. Abiturskript - 2.2.3 Ebenengleichung in Normalenform). Die Aufgabenstellung nennt als mögliches Ergebnis eine Gleichung der Ebene \(E\) in Normalenform in Koordinatendarstellung.
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
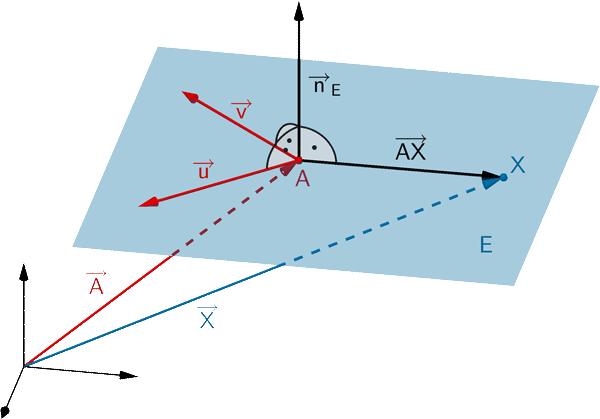
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Linear unabhängige Verbindungsvektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\) bestimmen:
Lineare (Un-)Abhängigkeit von zwei Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind
linear abhängig, wenn
\(\overrightarrow{a} \parallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} = k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
linear unabhängig, wenn
\(\overrightarrow{a} \nparallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} \neq k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
Lineare (Un-)Abhängigkeit von drei Vektoren
Drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind
linear abhängig, wenn
sie in einer Ebene liegen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat.
linear unabhängig, wenn
sie den Raum \(\mathbb R^{3}\) aufspannen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat.
Bei der Untersuchung der linearen (Un)Abhängigkeit dreier Vektoren spielt es keine Rolle, welche der drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) oder \(\overrightarrow{c}\) man als Linearkombination der beiden anderen Vektoren darzustellen versucht.
\(A(0|2|2)\), \(B(2|3|0)\), \(C(0|-2|4)\)
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 2 \\ 3 \\ 0 \end{pmatrix} - \begin{pmatrix} 0 \\ 2 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix}\]
\[\overrightarrow{AC} = \overrightarrow{C} - \overrightarrow{A} = \begin{pmatrix} 0 \\ -2 \\ 4 \end{pmatrix} - \begin{pmatrix} 0 \\ 2 \\ 2 \end{pmatrix} = \begin{pmatrix} 0 \\ -4 \\ 2 \end{pmatrix}\]
Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) ermitteln:
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\[\begin{align*} \overrightarrow{AB} \times \overrightarrow{AC} &= \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix} \times \begin{pmatrix} 0 \\ -4 \\ 2 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 1 & \cdot & 2 & - & (-2) & \cdot & (-4) \\ (-2) & \cdot & 0 & - & 2 & \cdot & 2 \\ 2 & \cdot & (-4) & - & 1 & \cdot & 0 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -6 \\ -4 \\ -8 \end{pmatrix} \\[0.8em] &= (-2) \cdot \begin{pmatrix} 3 \\ 2 \\ 4 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 3 \\ 2 \\ 4 \end{pmatrix}\]
Gleichung der Ebene \(E\) in Normalenform formulieren:
1. Möglichkeit: Ansatz mit der Normalenform in Vektordarstellung
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Es sei \(A\) der Aufpunkt der Ebene \(E\).
\[\overrightarrow{n}_{E} = \begin{pmatrix} 3 \\ 2 \\ 4 \end{pmatrix}, \; A(0|2|2)\]
\[\begin{align*} &E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \\[0.8em] &E \colon \begin{pmatrix} 3 \\ 2 \\ 4 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 2 \\ 2 \end{pmatrix} \right] = 0 \end{align*}\]
Ggf. wandelt man die Ebenengleichung in Normalenform in Vektordarstellung in die Koordinatendarstellung um. Hierfür wird das Skalarprodukt ausmultipliziert.
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \begin{pmatrix} 3 \\ 2 \\ 4 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 2 \\ 2 \end{pmatrix} \right] &= 0 \\[0.8em] 3 \cdot (x_{1} - 0) + 2 \cdot (x_{2} - 2) + 4 \cdot (x_{3} - 2) &= 0 \\[0.8em] 3x_{1} + 2x_{2} - 4 + 4x_{3} - 8 &= 0 \\[0.8em] 3x_{1} + 2x_{2} + 4x_{3} -12 &= 0 \end{align*}\]
\[\begin{align*}\Longrightarrow \quad &E \colon 3x_{1} + 2x_{2} + 4x_{3} - 12 = 0 \\[0.8em] &E \colon 3x_{1} + 2x_{2} + 4x_{3} = 12 \end{align*}\]
2. Möglichkeit: Ansatz mit der Normalenform in Koordinatendarstellung
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Es sei \(A\) der Aufpunkt der Ebene \(E\).
\[\overrightarrow{n}_{E} = \begin{pmatrix} 3 \\ 2 \\ 4 \end{pmatrix}, \; A(0|2|2)\]
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
\[E \colon 3x_{1} + 2x_{2} + 4x_{3} + n_{0} = 0\]
\[\begin{align*} A \in E \colon 3 \cdot 0 + 2 \cdot 2 + 4 \cdot 2 + n_{0} &= 0 \\[0.8em] 12 + n_{0} &= 0 & &| - 12 \\[0.8em] n_{0} &= -12 \end{align*}\]
\[\begin{align*}\Longrightarrow \quad &E \colon 3x_{1} + 2x_{2} + 4x_{3} - 12 = 0 \\[0.8em] &E \colon 3x_{1} + 2x_{2} + 4x_{3} = 12 \end{align*}\]
b) Koordinaten der Schnittpunkte der Ebene \(E\) mit den Koordinatenachsen und Veranschaulichung der Lage der Ebene \(E\) im Koordinatensystem
Die Schnittpunkte \(S_{1}\), \(S_{2}\) und \(S_{3}\) der Ebenen \(E\) mit der \(x_{1}\)-, \(x_{2}\)- bzw. \(x_{3}\)-Achse sind die Spurpunkte der Ebene \(E\). Jeweils zwei Koordinaten der Spurpunkte sind gleich Null (vgl. Abiturskript - 2.2.3 Ebenengleichung in Normalenform, Spurgerade einer Ebene).
Spurpunkt \(S_{1}\) (Schnittpunkt mit der \(x_{1}\)-Achse): \(S_{1}(x_{1}|0|0)\)
Spurpunkt \(S_{2}\) (Schnittpunkt mit der \(x_{2}\)-Achse): \(S_{2}(0|x_{2}|0)\)
Spurpunkt \(S_{3}\) (Schnittpunkt mit der \(x_{3}\)-Achse): \(S_{3}(0|0|x_{3})\)
Die jeweils fehlende Koordinate lässt sich durch Einsetzen der Koordinaten der Spurpunkte in die Gleichung der Ebenen \(E\) (vgl. Teilaufgabe a) berechnen.
\[E \colon 3x_{1} + 2x_{2} + 4x_{3} = 12\]
\[\begin{align*} S_{1}(x_{1}|0|0) \in E \colon 3x_{1} + 2 \cdot 0 + 4 \cdot 0 &= 12 \\[0.8em] 3x_{1} &= 12 &&| : 3 \\[0.8em] x_{1} &= 4 \end{align*}\]
\[\Longrightarrow \quad S_{1}(4|0|0)\]
\[\begin{align*} S_{2}(0|x_{2}|0) \in E \colon 3 \cdot 0 + 2x_{2} + 4 \cdot 0 &= 12 \\[0.8em] 2x_{2} &= 12 &&| : 2 \\[0.8em] x_{2} &= 6 \end{align*}\]
\[\Longrightarrow \quad S_{2}(0|6|0)\]
\[\begin{align*} S_{3}(0|0|x_{3}) \in E \colon 3 \cdot 0 + 2 \cdot 0 + 4x_{3} &= 12 \\[0.8em] 4x_{3} &= 12 &&| : 4 \\[0.8em] x_{3} &= 3 \end{align*}\]
\[\Longrightarrow \quad S_{3}(0|0|3)\]
Veranschaulichung der Lage der Ebene \(E\) im Koordinatensystem:
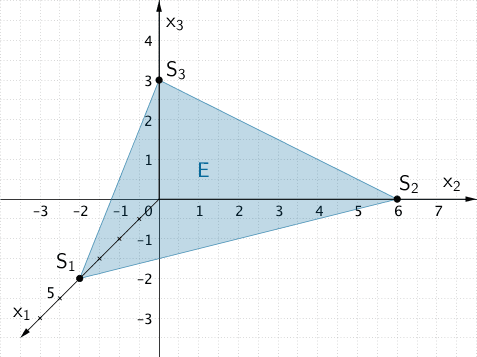
Durch Einzeichnen der Spukpunkte \(S_{1}\), \(S_{2}\) und \(S_{3}\) der Ebene \(E\) lässt sich die Lage der Ebene \(E\) im Koordinatensystem veranschaulichen.
c) Gleichung der Schnittgeraden \(s\) der Ebene \(E\) und der \(x_{2}x_{3}\)-Ebene
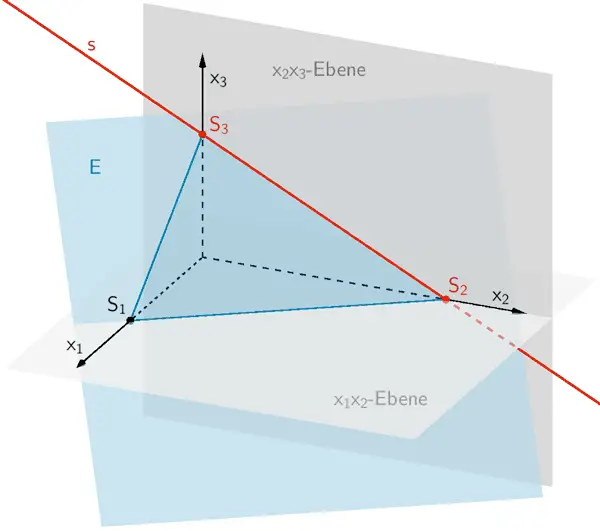
Die Schnittgeraden \(s\) der Ebene \(E\) und der \(x_{2}x_{3}\)-Ebene entspricht der Spurgeraden \(S_{2}S_{3}\) der Ebene \(E\).
Die Spurpunkte \(S_{2}\) und \(S_{3}\) legen also die Schnittgerade \(s\) fest. Eine Gleichung der Schnittgeraden \(s\) in Parameterform lässt sich daher beispielsweise mit dem Spurpunkt \(S_{2}\) als Aufpunkt und dem Verbindungsvektor \(\overrightarrow{S_{2}S_{3}}\) als Richtungsvektor angeben.
Gleichung einer Gerad / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[s \colon \overrightarrow{X} = \overrightarrow{S_{2}} + \lambda \cdot \overrightarrow{S_{2}S_{3}}; \; \lambda \in \mathbb R\]
\[\overrightarrow{S_{2}S_{3}} = \overrightarrow{S_{3}} - \overrightarrow{S_{2}} = \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix} - \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix}\]
\[\Longrightarrow \quad s \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix}; \; \lambda \in \mathbb R\]
Alternativer Lösungsweg:
(vgl. Abiturskript - 2.3.3 Lagebeziehung von Ebenen, Bestimmung der Schnittgeraden zweier Ebenen)
\[E \colon 3x_{1} + 2x_{2} + 4x_{3} = 12\]
\(x_{2}x_{3}\text{-Ebene}\colon x_{1} = 0\)
Die Schnittgerade \(s\) beschreibt die Menge aller Punkte \(X\), welche sowohl in der Ebene \(E\) als auch in der \(x_{2}x_{3}\)-Ebene liegen. Die beiden Ebenengleichungen in Normalenform in Koordinatendarstellung bilden somit ein lineares Gleichungssystem.
\[\Longrightarrow \enspace \left\{ \begin{align*} \text{I} & & & 3x_{1} + 2x_{2} + 4x_{3} = 12 \\[0.8em] \text{II} & & \wedge \enspace & \enspace x_{1} = 0 \end{align*} \right.\]
Gleichung II in Gleichung I eingesetzt, ergibt eine Gleichung mit zwei Unbekannten \((x_{2}, x_{3})\).
\[\text{II in I} \colon 2x_{2} + 4x_{3} = 12\]
Die Gleichung kann nur in Abhängigkeit einer frei wählbaren Variablen gelöst werden. Eine der Koordinaten \(x_{2}\) oder \(x_{3}\) wird mit einem Parameter besetzt. Beispielsweise wählt man \(x_{3} = \lambda\) mit \(\lambda \in \mathbb R\) und gibt die Koordinate \(x_{2}\) in Abhängigkeit des Parameters \(\lambda\) an.
Damit lassen sich alle drei Koordinaten \(x_{1}\), \(x_{2}\) und \(x_{3}\) des Ortsvektors \(\overrightarrow{X}\) eines beliebigen Punktes \(X\) der Schnittgeraden \(s\) in Abhängigkeit des Parameters \(\lambda\) beschreiben. Durch Umformen erhält man eine Gleichung der Schnittgeraden \(s\) in Parameterform.
\[x_{3} = \lambda; \; \lambda \in \mathbb R\]
\[\begin{align*}2x_{2} + 4 \lambda &= 12 &&| -4\lambda \\[0.8em] 2x_{2} &= 12 - 4\lambda &&| : 2 \\[0.8em] x_{2} &= 6 - 2\lambda \end{align*}\]
Mit \(x_{1} = 0\), \(x_{2} = 6 - 2\lambda\) und \(x_{3} = \lambda\) ergibt sich der Ortsvektor \(\overrightarrow{X}\) eines beliebigen Punktes \(X\) der Schnittgeraden \(s\) zu:
\[\overrightarrow{X} = \begin{pmatrix} 0 \\ 6 - 2\lambda \\ \lambda \end{pmatrix}; \; \lambda \in \mathbb R\]
Abschließend wird der Ortsvektor \(\overrightarrow{X}\) in der nach dem Ortsvektor des Aufpunkts und dem Richtungsvektor getrennten Schreibweise \(\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\) formuliert.
Gleichung einer Gerad / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[\overrightarrow{X} = \begin{pmatrix} 0 \\ 6 - 2\lambda \\ \lambda \end{pmatrix} = \begin{pmatrix} 0 + 0\lambda \\ 6 - 2\lambda \\ 0 + 1\lambda \end{pmatrix} = \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ -2 \\ 1 \end{pmatrix}\]
\[\Longrightarrow \quad s \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ -2 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]
d) Koordinaten des Punktes \(S'\), der durch Spiegelung des Punktes \(S_{1}\) an der Geraden \(s\) hervorgeht
(vgl. Abiturskript - 2.6.2 Spiegelung eines Punktes an einer Geraden)
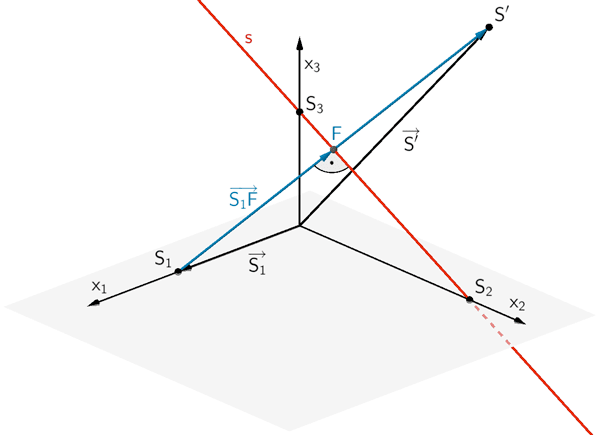
Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(S_{1}\) auf die Gerade \(s\) (vgl. Teilaufgabe c). Die Entstehung des Punktes \(S'\), der durch Spiegelung des Punktes \(S_{1}\) an der Geraden \(s\) hervorgeht, lässt sich auf die Spiegelung des Punktes \(S_{1}\) am Lotfußpunkt \(F\) zurückführen (vgl. Abiturskript - 2.6.1 Spiegelung eines Punktes an einem Punkt). Der Ortsvektor \(\overrightarrow{S'}\) ergibt sich durch Vektoraddition:
\[\overrightarrow{S'} = \overrightarrow{S_{1}} + 2 \cdot \overrightarrow{S_{1}F}\]
oder
\[\overrightarrow{S'} = \overrightarrow{F} + \overrightarrow{S_{1}F}\]
Es gibt mehrere Möglichkeiten, den Verbindungsvektor \(\overrightarrow{S_{1}F}\) bzw. den Ortsvektor \(\overrightarrow{F}\) zu ermitteln. Nachfolgend werden drei Lösungsansätze aus der analytischen Geometrie vorgestellt und ein Lösungsansatz, der die Differentialrechnung anwendet.
1. Möglichkeit: Skalarprodukt orthogonaler (senkrechter) Vektoren anwenden
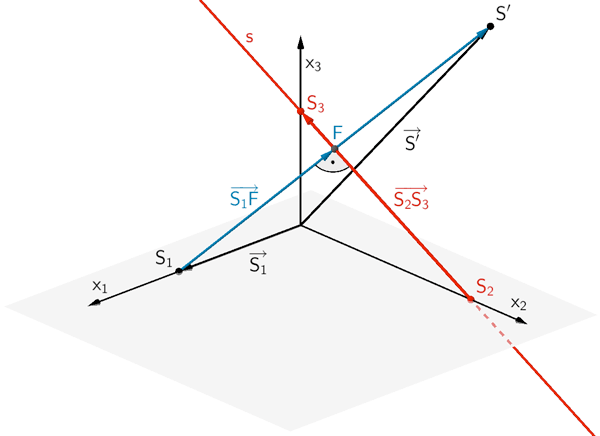
Der Verbindungsvektor \(\overrightarrow{S_{2}S_{3}}\) (oder ein reelles Vielfaches davon) ist ein Richtungsvektor der Geraden \(s\) (vgl. Teilaufgabe c). Der Richtungsvektor der Geraden \(s\) und der Verbindungsvektor \(\overrightarrow{S_{1}F}\) sind zueinander senkrecht. Folglich ist das Skalarprodukt der Vektoren gleich Null (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{S_{2}S_{3}} \perp \overrightarrow{S_{1}F} \quad \Longleftrightarrow \quad \overrightarrow{S_{2}S_{3}} \circ \overrightarrow{S_{1}F} = 0\]
Der Verbindungsvektor \(\overrightarrow{S_{2}S_{3}}\) ist aus Teilaufgabe c bereits bekannt.
\[\overrightarrow{S_{2}S_{3}} = \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix}\]
Der Verbindungsvektor \(\overrightarrow{S_{1}F}\) lässt sich mit \(F \in s\) in Abhängigkeit des Parameters \(\lambda\) der Geraden \(s\) beschreiben.
\[s \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[F \in s \colon \overrightarrow{F} = \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix} = \begin{pmatrix} 0 \\ 6 - 6\lambda \\ 3\lambda \end{pmatrix}\]
MIt \(\overrightarrow{S_{1}} = \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix}\) (vgl. Teilaufgabe b) folgt:
\[\overrightarrow{S_{1}F} = \overrightarrow{F} - \overrightarrow{S_{1}} = \begin{pmatrix} 0 \\ 6 - 6\lambda \\ 3\lambda \end{pmatrix} - \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} -4 \\ 6 - 6\lambda \\ 3\lambda \end{pmatrix}\]
Skalarprodukt orthogonaler Vektoren anwenden:
das Skalarprodukt der othogonalen Vektoren \(\overrightarrow{S_{2}S_{3}}\) und \(\overrightarrow{S_{1}F}\) liefert genau den Wert des Parameters \(\lambda\), der den Verbindungsvektor \(\overrightarrow{S_{1}F}\) bzw. den Ortsvektor \(\overrightarrow{F}\) festlegt.
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \overrightarrow{S_{2}S_{3}} \circ \overrightarrow{S_{1}F} &= 0 \\[0.8em] \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix} \circ \begin{pmatrix} -4 \\ 6 - 6\lambda \\ 3\lambda \end{pmatrix} &= 0 \\[0.8em] 0 \cdot (-4) + (-6) \cdot (6 - 6\lambda) + 3 \cdot 3\lambda &= 0 \\[0.8em] -36 + 36\lambda + 9\lambda &= 0 \\[0.8em] -36 + 45\lambda &= 0 &&| + 36 \\[0.8em] 45\lambda &= 36 &&| : 45 \\[0.8em] \lambda &= \frac{36}{45} \\[0.8em] &= \frac{4}{5} \\[0.8em] &= 0{,}8 \end{align*}\]
Verbindungsvektor \(\overrightarrow{S_{1}F}\) oder Ortsvektor \(\overrightarrow{F}\) berechnen:
\[\overrightarrow{S_{1}F} = \begin{pmatrix} -4 \\ 6 - 6 \cdot 0{,}8 \\ 3 \cdot 0{,}8 \end{pmatrix} = \begin{pmatrix} -4 \\ 1{,}2 \\ 2{,}4 \end{pmatrix}\]
\[\overrightarrow{F} = \begin{pmatrix} 0 \\ 6 - 6 \cdot 0{,}8 \\ 3 \cdot 0{,}8 \end{pmatrix} = \begin{pmatrix} 0 \\ 1{,}2 \\ 2{,}4 \end{pmatrix}\]
Koordinaten des Punktes \(S'\) berechnen:
\[\overrightarrow{S'} = \overrightarrow{S_{1}} + 2 \cdot \overrightarrow{S_{1}F} = \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} + 2 \cdot \begin{pmatrix} -4 \\ 1{,}2 \\ 2{,}4 \end{pmatrix} = \begin{pmatrix} -4 \\ 2{,}4 \\ 4{,}8 \end{pmatrix}\]
\[\Longrightarrow \quad S'(-4|2{,}4|4{,}8)\]
oder
\[\overrightarrow{S'} = \overrightarrow{F} + \overrightarrow{S_{1}F} = \begin{pmatrix} 0 \\ 1{,}2 \\ 2{,}4 \end{pmatrix} + \begin{pmatrix} -4 \\ 1{,}2 \\ 2{,}4 \end{pmatrix} = \begin{pmatrix} -4 \\ 2{,}4 \\ 4{,}8 \end{pmatrix}\]
\[\Longrightarrow \quad S'(-4|2{,}4|4{,}8)\]
2. Möglichkeit: Hilfsebene aufstellen
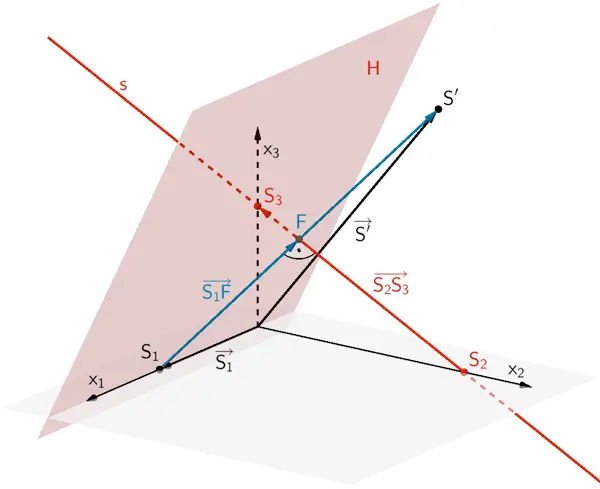
Die Hilfsebene \(H\), welche den Punkt \(S_{1}\) enthält (\(S_{1} \in H\)) und senkrecht zur Geraden \(s\) liegt (\(H \perp s\)), schneidet die Gerade \(s\) im Lotfußpunkt \(F\). Der Richtungsvektor \(\overrightarrow{S_{2}S_{3}}\) der Geraden \(s\) (vgl. Teilaufgabe c) ist ein Normalenvektor der Hilfsebene \(H\).
Der Verbindungsvektor \(\overrightarrow{S_{1}F}\) lässt sich in Abhängigkeit des Parameters \(\lambda\) der Geraden \(s\) beschreiben (vgl. 1. Möglichkeit).
\[\overrightarrow{S_{1}F} = \begin{pmatrix} -4 \\ 6 - 6\lambda \\ 3\lambda \end{pmatrix}\]
Hilfsebene \(H\) austellen (vgl. Abiturskript - 2.3.4 Lotgeraden und orthogonale Ebenen):
\(S_{1} \in H\); \(H \perp s\)
\(\overrightarrow{S_{2}S_{3}} = \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix}\), \(\overrightarrow{S_{1}} = \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix}\) (vgl. Teilaufgabe b, c)
\[H \colon \overrightarrow{S_{2}S_{3}} \circ (\overrightarrow{X} - \overrightarrow{S_{1}})\]
\[H \colon \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix}\right] = 0\]
Schneidet man die Gerade \(s\) mit der Hilfsebene \(H\), erhält man genau den Wert des Parameters \(\lambda\), der den Verbindungsvektor \(\overrightarrow{S_{1}F}\) bzw. den Ortsvektor \(\overrightarrow{F}\) festlegt (vgl. Abiturskript - 2.3.2 Lagebeziehung von Gerade und Ebene, Bestimmung des Schnittpunkts). Hierfür wird der Ortsvektor \(\overrightarrow{X}\) der Gleichung der Geraden \(s\) in die Gleichung der Hilfsebene \(H\) eingesetzt und die Gleichung nach dem Parameter \(\lambda\) aufgelöst.
\[s \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix} = \begin{pmatrix} 0 \\ 6 - 6\lambda \\ 3\lambda \end{pmatrix}; \; \lambda \in \mathbb R\]
\[H \colon \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix}\right] = 0\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*}s \cap H \colon \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix} \circ \left[ \begin{pmatrix} 0 \\ 6 - 6\lambda \\ 3\lambda \end{pmatrix} - \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix}\right] &= 0 \\[0.8em] \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix} \circ \begin{pmatrix} -4 \\ 6 - 6\lambda \\ 3\lambda \end{pmatrix} &= 0 \\[0.8em] 0 \cdot (-4) + (-6) \cdot (6 - 6\lambda) + 3 \cdot 3\lambda &= 0 \\[0.8em] -36 + 36\lambda + 9\lambda &= 0 \\[0.8em] -36 + 45\lambda &= 0 &&| + 36 \\[0.8em] 45\lambda &= 36 &&| : 45 \\[0.8em] \lambda &= \frac{36}{45} \\[0.8em] &= \frac{4}{5} \\[0.8em] &= 0{,}8 \end{align*}\]
Für die Berechnung der Koordinaten des Punktes \(S'\) vgl. 1. Möglichkeit.
3. Möglichkeit: Differentialrechnung anwenden (Extremwertaufgabe)
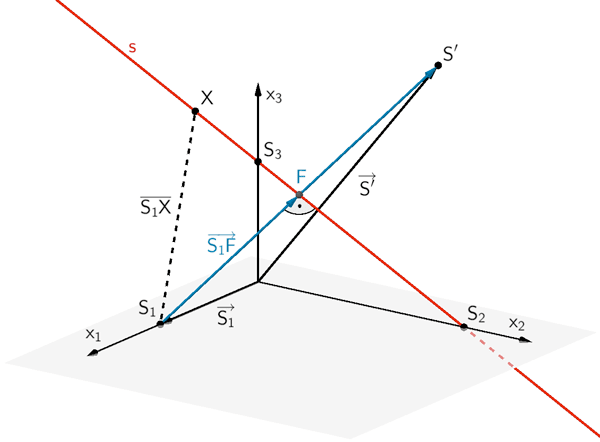
Die Länge der Strecke \([S_{1}X]\) zwischen dem Punkt \(S_{1}\) und einem Beliebigen Punkt \(X\) auf der Geraden \(s\) \((X \in s)\) ist gleich dem Betrag des Verbindungsvektors \(\overrightarrow{S_{1}X}\).
\[\overline{S_{1}X} = \vert \overrightarrow{S_{1}X} \vert\]
Für \(X = F\) ist die Lage der Strecke \([S_{1}X]\) minimal. Folglich muss die erste Ableitung \(\overline{S_{1}X}'\) gleich Null sein (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte). Der Nachweis der Art des Extremwerts kann entfallen, denn für \(X \neq F\) nimmt die Länge der Strecke \([S_{1}X]\) einen beliebig großen Wert an. Somit existiert keine maximale Länge der Strecke \([S_{1}X]\).
Der Verbindungsvektor \(\overrightarrow{S_{1}X}\) lässt sich mit \(X \in s\) in Abhängigkeit des Parameters \(\lambda\) der Geraden \(s\) beschreiben (vgl. 1. Möglichkeit, Verbindungsvektor \(\overrightarrow{S_{1}F}\)).
\[\overrightarrow{S_{1}X} = \begin{pmatrix} -4 \\ 6 - 6\lambda \\ 3\lambda \end{pmatrix}\]
Länge der Strecke \([S_{1}X]\) in Abhängigkeit des Parameters \(\lambda\) beschreiben:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}\overline{S_{1}X} &= \vert \overrightarrow{S_{1}X} \vert \\[0.8em] &= \left| \begin{pmatrix} -4 \\ 6 - 6\lambda \\ 3\lambda \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-4)^{2} + (6 - 6\lambda)^{2} +(3\lambda)^{2}} \\[0.8em] &= \sqrt{16 + 36 - 72\lambda + 36{\lambda}^{2} + 9{\lambda}^{2}} \\[0.8em] &= \sqrt{45{\lambda}^{2} -72\lambda + 52} \end{align*}\]
Notwendige Bedingung \(\overline{S_{1}X}'(\lambda) = 0\) für minimale Länge der Strecke \([S_{1}X]\):
\[\begin{align*}\overline{S_{1}X}'(\lambda) &= 0 \\[0.8em] \left( \sqrt{45{\lambda}^{2} - 72\lambda + 52} \right)' &= 0 \end{align*}\]
Da der Wert einer Wurzel minimal ist, wenn der Wert des Radikanden (Ausdruck unter der Wurzel) minimal ist, genügt es, den Radikanden zu betrachten und dessen erste Ableitung gleich Null zu setzen.
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*}\Longrightarrow \quad \left( 45{\lambda}^{2} - 72\lambda + 52 \right)' &= 0 \\[0.8em] 90\lambda - 72 &= 0 &&| + 72 \\[0.8em] 90\lambda &= 72 &&| : 90 \\[0.8em] \lambda &= \frac{72}{90} \\[0.8em] &= \frac{4}{5} \\[0.8em] &= 0{,}8 \end{align*}\]
Für \(\lambda = 0{,}8\) ist die Länge der Strecke \([S_{1}X]\) minimal, d.h. es gilt \([S_{1}X] = [S_{1}F]\).
Die Berechnung der Koordinaten des Punktes \(S'\) erfolgt wie bei der 1. Möglichkeit beschrieben.
4. Möglichkeit: Lotgerade zur Geraden \(s\) durch Punkt \(S_{1}\) aufstellen
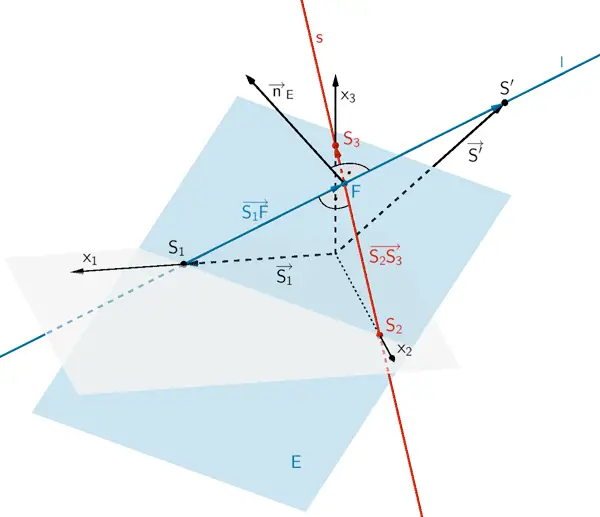
Betrachtet wird die Lotgerade \(l\) zur Geraden \(s\) durch den Punkt \(S_{1}\). Die Lotgerade \(l\) schneidet die Gerade \(s\) im Lotfußpunkt \(F\). Da die Lotgerade \(l\) in der Ebene \(E\) liegt (vgl, Teilaufgabe a), ist das Vektorprodukt aus dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) und dem Richtungsvektor \(\overrightarrow{S_{2}S_{3}}\) der Geraden \(s\) ein Richtungsvektor der Lotgeraden \(l\).
Richtungsvektor der Lotgerade \(l\) zur Geraden \(s\) ermitteln:
\(\overrightarrow{n}_{E} = \begin{pmatrix} 3 \\ 2 \\ 4 \end{pmatrix}\), \(\overrightarrow{S_{2}S_{3}} = \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix}\) (vgl. Teilaufgabe a, c)
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\[\begin{align*} \overrightarrow{n}_{E} \times \overrightarrow{S_{2}S_{3}} &= \begin{pmatrix} 3 \\ 2 \\ 4 \end{pmatrix} \times \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 2 & \cdot & 3 & - & 4 & \cdot & (-6) \\ 4 & \cdot & 0 & - & 3 & \cdot & 3 \\ 3 & \cdot & (-6) & - & 2 & \cdot & 0 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 30 \\ -9 \\ -18 \end{pmatrix} \\[0.8em] &= 3 \cdot \begin{pmatrix} 10 \\ -3 \\ -6 \end{pmatrix} \end{align*}\]
Der Vektor \(\begin{pmatrix} 10 \\ -3 \\ -6 \end{pmatrix}\) ist ein Richtungsvektor der Lotgeraden \(l\).
Mit \(\overrightarrow{S_{1}} = \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix}\) (vgl. Teilaufgabe b) folgt:
\[l \colon \overrightarrow{X} = \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} 10 \\ -3 \\ -6 \end{pmatrix}; \; \mu \in \mathbb R\]
Schneidet man nun die Lotgerade \(l\) mit der Geraden \(s\) erhält man genau den Wert des Parameters \(\lambda\) bzw. des Parameters \(\mu\), der den Verbindungsvektor \(\overrightarrow{S_{1}F}\) bzw. den Ortsvektor \(\overrightarrow{F}\) festlegt. Hierfür werden die Ortsvektoren \(\overrightarrow{X}\)der Geradengleichungen gleichgesetzt.
\[l \colon \overrightarrow{X} = \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} 10 \\ -3 \\ -6 \end{pmatrix}; \; \mu \in \mathbb R\]
\[s \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[\begin{align*} \overrightarrow{X}_{l} &= \overrightarrow{X}_{s} \\[0.8em] \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} 10 \\ -3 \\ -6 \end{pmatrix} &= \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ -6 \\ 3 \end{pmatrix} \end{align*}\]
Zeilenweise gelesen, ergibt die Vektorgleichung ein (überbestimmtes) lineares Gleichungssystem mit den beiden Unbekannten \(\lambda\) und \(\mu\).
\begin{align*} \text{I} & & & 4 + 10\mu = 0 \quad \Longrightarrow \quad \mu = -\frac{4}{10} = -0{,}4 \\[0.8em] \text{II} & & \wedge \enspace & \quad -3\mu = 6 - 6\lambda \\[0.8em] \text{III} & & \wedge \enspace & \quad -6\mu = \quad \enspace \; 3\lambda \quad \Longrightarrow \quad \lambda = -2\mu \end{align*}
\[\mu = -0{,}4 \; \text{in III}\colon \; \lambda = (-2) \cdot (-0{,}4) = 0{,}8\]
\[\begin{align*}\mu = -0{,}4, \; \lambda = 0{,}8 \; \text{in II}\colon \; (-3) \cdot (-0{,}4) &= 6 - 6 \cdot 0{,}8 \\[0.8em] 1{,}2 &= 6 - 4{,}8 \\[0.8em] 1{,}2 &= 1{,}2 \quad (\text{w}) \end{align*}\]
\(\lambda = 0{,}8\), \(\mu = -0{,}4\) ist eindeutige Lösung de Gleichungssystems.
Die Berechnung der Koordinaten des Punktes \(S'\) erfolgt wie bei der 1. Möglichkeit beschrieben.
Mit \(F \in l\) kann für die Berechnung des Ortsvektors \(\overrightarrow{F}\) auch \(\mu = -0{,}4\) in die Gleichung der Lotgeraden \(l\) eingesetzt werden.
\[F \in l \colon \overrightarrow{F} = \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} - 0{,}4 \cdot \begin{pmatrix} 10 \\ -3 \\ -6 \end{pmatrix} = \begin{pmatrix} 0 \\ 1{,}2 \\ 2{,}4 \end{pmatrix}\]

