Die Gerade \(g\) schneidet \(G_{f}\) in den Punkten \(W\) und \((2|0)\).
Zeichnen Sie unter Berücksichtigung der bisherigen Ergebnisse \(G_{f}\) sowie die Gerade \(g\) in ein Koordinatensystem ein. Geben Sie die Gleichung der Geraden \(g\) an.
(4 BE)
Lösung zu Teilaufgabe 1c
Zeichnen eines Funktionsgraphen
\[f(x) = x^{4} - 2x^{3}\,; \enspace D = \mathbb R\]
\[W(1|-1), (2|0) \in g\]
Zeichnung von \(G_{f}\) sowie der Geraden \(g\) unter Berücksichtigung der bisherigen Ergebnisse
Bisherige Ergebnisse aus den Teilaufgaben 1a und 1b:
Der Punkt \(O\,(0|0)\) ist Terrassenpunkt von \(G_{f}\).
Der Punkt \(W (1|-1)\) ist Wendepunkt von \(G_{f}\).
Der Punkt \(TiP \left( \frac{3}{2} \bigg \vert -\frac{27}{16} \right)\) ist Tiefpunkt von \(G_{f}\)
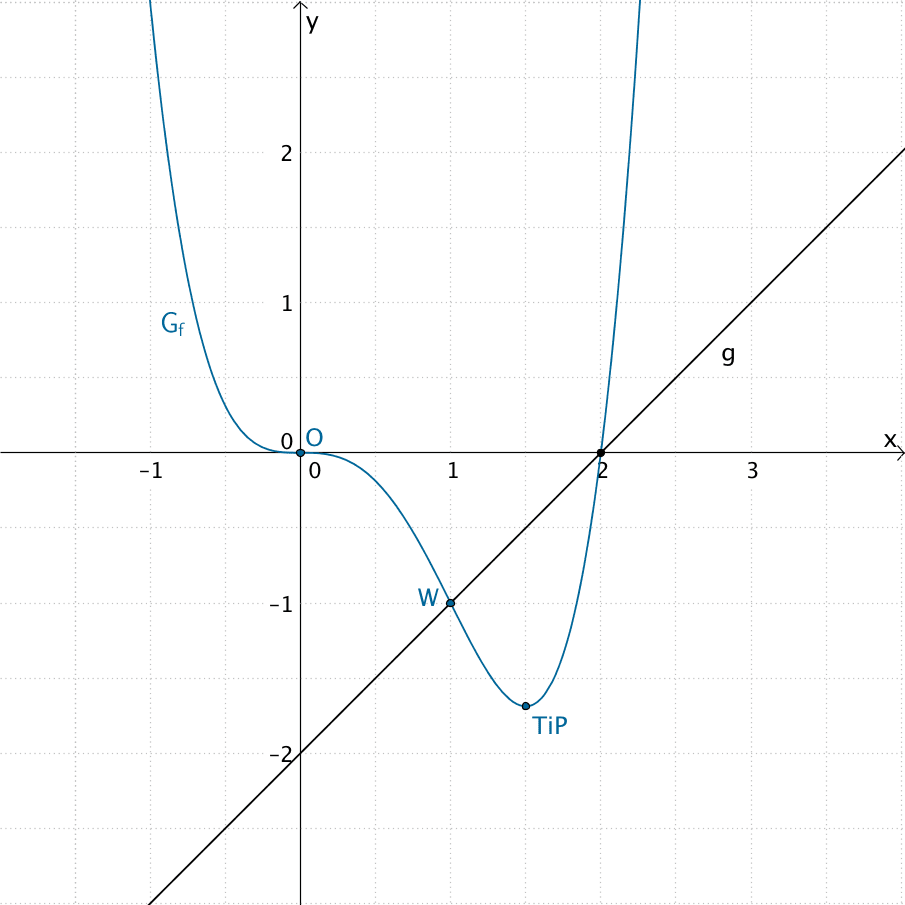
Verlauf des Graphen der Funktion \(f\) sowie der Geraden \(g\)
Gleichung der Geraden \(g\)
Allgemeine Geradengleichung
\[y = mx + t\]
Wobei \(m\) die Steigung und \(t\) der \(y\)-Achsenabschnitt der Geraden ist.
Anhand der beiden Punkte \(W (1|-1)\) und \((2|0)\) kann der Steigungsfaktor der Geraden \(g\) zu \(m = 1\) auf graphischem Wege entnommen werden. Der \(y\)-Achsenabschnitt \(t = -2\) lässt sich ebenfalls aus der Zeichnung ablesen.
\[\Longrightarrow \quad g \colon y = x - 2\]
Rechnerische Lösung:
\[W (1|-1), (2|0) \in g\]
Allgemeine Geradengleichung
\[y = mx + t\]
Wobei \(m\) die Steigung und \(t\) der \(y\)-Achsenabschnitt der Geraden ist.
\[m_{g} = \frac{\Delta y}{\Delta x} = \frac{0 - (-1)}{2 - 1} = 1\]
\[\Longrightarrow \quad g \colon y = x + t\]
\[\begin{align*} (2|0) \in g \colon 0 &= 2 + t & &| -2 \\[0.8em] -2 &= t \end{align*}\]
\[\Longrightarrow \quad g \colon y = x - 2\]
Oder mit der Punktsteigungsform der Geradengleichung von \(g\) und z.B. dem Punkt \(W(1|-1)\):
Geradengleichung, Punktsteigungsform
\[y = m (x -x_{0}) + y_{0}\]
Wobei \(m\) die Steigung der Geraden und \(P\,(x_{0}|y_{0})\) ein Punkt auf der Geraden ist.
\[g \colon y = m \cdot (x -x_{W}) + y_{W}\]
\[m_{g} = \frac{\Delta y}{\Delta x} = \frac{0 - (-1)}{2 - 1} = 1\]
\[\begin{align*} g\colon y &= m \cdot (x -x_{W}) + y_{W} \\[0.8em] y &= 1 \cdot (x - 1) - 1 \\[0.8em] y &= x - 1 - 1 \\[0.8em] y &= x - 2 \end{align*}\]
Oder durch Aufstellen eines linearen Gleichungssystems:
Allgemeine Geradengleichung
\[y = mx + t\]
Wobei \(m\) die Steigung und \(t\) der \(y\)-Achsenabschnitt der Geraden ist.
\[g \colon y = mx + t\]
\[\begin{align*} W(1|-1) \in g \colon & & \text{I} & & -1 &= 1 \cdot m + 1 \\[0.8em] (2|0) \in g \colon & & \text{II} & & \wedge \quad 0 &= 2 \cdot m + t \\[2.4em] & & \text{II} - \text{I} & & 1 &= m \\[2.4em] & & m = 1 \; \textsf{in} \; \text{II} & & 0 &= 2 \cdot 1 + t & &| -2 \\[0.8em] & & & & -2 &= t \end{align*}\]
\[\Longrightarrow \quad g \colon y = x - 2\]

