Weisen Sie nach, dass die Ereignisse \(C\) und \(D\) abhängig sind.
(2 BE)
Lösung zu Teilaufgabe 2b
Stochastische (Un)Abhängigkeit von zwei Ereignissen
Zwei Ereignisse \(A\) und \(B\) heißen stochastisch unabhängig, wenn
\(P(A) \cdot P(B) = P(A \cap B)\) gilt. (vgl. Merkhilfe) *
Andernfalls heißen die Ereignisse \(A\) und \(B\) stochastisch abhängig.
Sind zwei Ereignisse \(A\) und \(B\) stochastisch unabhängig, beeinflusst das Eintreten des Ereignisses \(A\) nicht das Eintreten des Ereignisses \(B\) und umgekehrt.
* Oder wenn
\(P(\overline{A}) \cdot P(B) = P(\overline{A} \cap B)\) bzw.
\(P(A) \cdot P(\overline{B}) = P(A \cap \overline{B})\) bzw.
\(P(\overline{A}) \cdot P(\overline{B}) = P(\overline{A} \cap \overline{B})\) gilt.
Die Ereignisse \(C\) und \(D\) sind abhängig, wenn gilt:
\[P(C \cap D) \neq P(C) \cdot P(D)\]
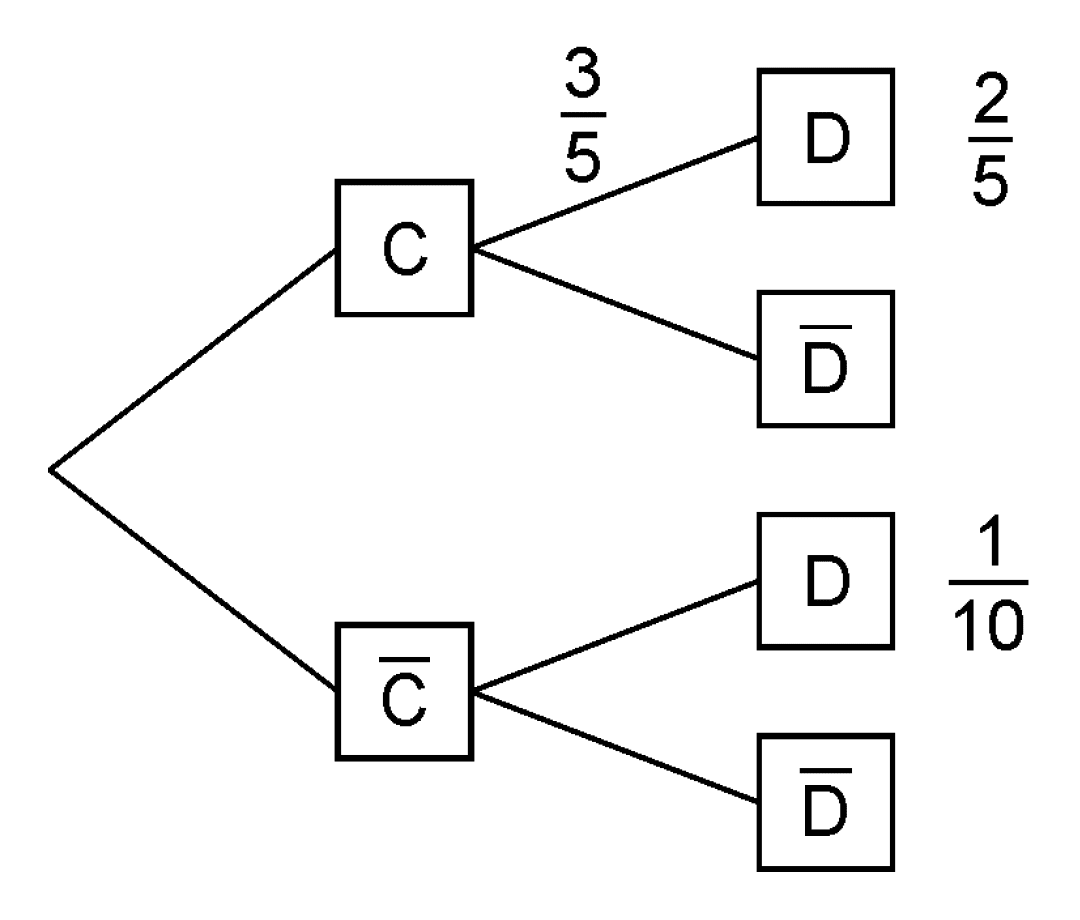
Dem Baumdiagramm entnimmt man die Schnittmengenwahrscheinlichkeiten \(P(C \cap D)\) und \(P(\overline{C}) \cap D\) sowie die bedingte Wahrscheinlichkeit \(P_{C}(D)\):
\[P(C \cap D) = \frac{2}{5}\,; \quad P(\overline{C} \cap D) = \frac{1}{10}\,; \quad P_{C}(D) = \frac{3}{5}\]
Wahrscheinlichkeit \(P(D)\) berechnen (siehe auch Teilaufgabe 2a):
\[\begin{align*} P(D) &= P(C \cap D) + P(\overline{C} \cap D) \\[0.8em] &= \frac{2}{5} + \frac{1}{10} \\[0.8em] &= \frac{4}{10} + \frac{1}{10} \\[0.8em] &= \frac{1}{2}\end{align*}\]
Wahrscheinlichkeit \(P(C)\) berechnen:
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\[\begin{align*} P_{C}(D) &= \frac{P(C \cap D)}{P(C)} & &| \; \cdot P(C) \enspace : P_{C}(D) \\[0.8em] P(C) &= \frac{P(C \cap D)}{P_{C}(D)} \\[0.8em] &= \frac{\frac{2}{5}}{\frac{3}{5}} = \frac{2}{5} \cdot \frac{5}{3} = \frac{2}{3} \end{align*}\]
Abhängigkeit der Ereignisse \(C\) und \(D\) prüfen:
\[P(C \cap D) = \frac{2}{5}\]
\[P(C) \cdot P(D) = \frac{2}{3} \cdot \frac{1}{2} = \frac{1}{3}\]
\[\begin{align*}\Longrightarrow \quad P(C \cap D) &\neq P(C) \cdot P(D) \\[0.8em] \frac{2}{5} &\neq \frac{1}{3} \end{align*}\]
\(\Longrightarrow \quad\) Die Ereignisse \(C\) und \(D\) sind abhängig.


