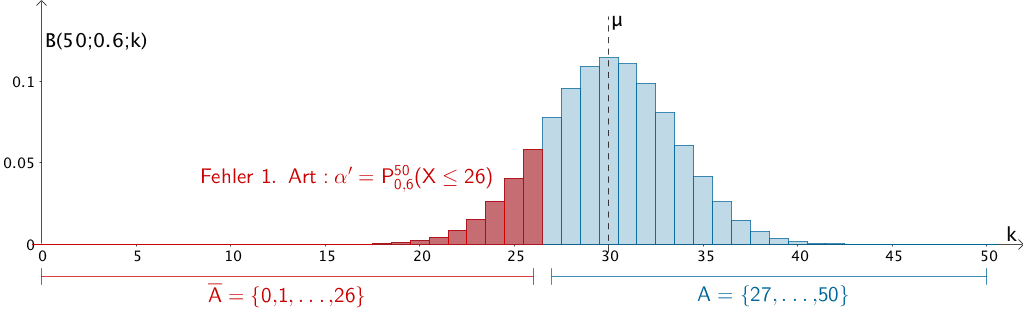Hypothesentest und Alternativtest
Ein Hypothesentest formuliert eine Vermutung (Hypothese) zu einem umfangreichen, nicht exakt zu bestimmenden statistischen Sachverhalt und testet anhand einer Stichprobe, ob die Hypothese angenommen oder abgelehnt wird.
Soll beispielsweise untersucht werden, wie viele Einwohner Deutschlands Raucher sind, ist es nicht möglich alle Einwohner dazu zu befragen. Stattdessen wird anhand einer repräsentativen statistischen Erhebung (Befragung) eine Aussage getroffen. Ob sich der Anteil der Raucher der Bevölkerung Deutschlands mit der Zeit ändert, lässt sich dann zu einem späteren Zeitpunkt überprüfen, indem eine Vermutung formuliert und getestet wird.
In der Regel bezieht sich die Hypothese auf eine unbekannte Wahrscheinlichkeit \(p\) eines Ereignisses bei einem Zufallsexperiment. Dann beschreiben \(n\) einzelne Ergebnisse der Stichprobe eine Bernoulli-Kette der Länge \(\boldsymbol{n}\) und die Zufallsgröße \(X\) gibt an, wie oft das Ereignis bei der Stichprobe eintritt. Die Zufallsgröße \(X\) ist somit nach \(B(n;p)\) binomialverteilt. Die Zufallsgröße \(X\) wird auch als Testgröße \(X\) bezeichnet.
Werden zwei sich gegenseitig ausschließende Hypothesen betrachtet, spricht man von einem Alternativtest. Die Nullhypothese \(\boldsymbol{H_{0}}\) bezieht sich dabei meist auf einen bisher gültigen Kenntnisstand, welcher nicht grundlos verworfen werden soll. Die Gegenhypothese \(\boldsymbol{H_{1}}\) formuliert eine neue Vermutung, welche es zu überprüfen gilt.
Eine Entscheidungsregel gibt für jedes mögliche Stichprobenergebnis \(X = x_{i}\) mit \(x_{i} \in \{0, 1, 2, ..., n\}\) an, welche der beiden Hypothesen angenommen bzw. abgelehnt wird. Hierfür wird vorab der Durchführung des Alternativtests ein Annahmebereich \(\boldsymbol{A}\) mit \(A \subseteq \{0, 1, 2, ..., n\}\) und ein Ablehnungsbereich \(\boldsymbol{\overline{A}}\) mit \(\overline{A} = \{0, 1, 2, ..., n\} \, \backslash \, A\) für die Nullhypothese festgelegt. Liegt das Stichprobenergebnis im Annahmebereich der Nullhypothese, wird diese angenommen bzw. beibehalten. Liegt das Stichprobenergebnis im Ablehnungsbereich der Nullhypothese, wird diese abgelehnt und die Gegenhypothese angenommen.
Fehler 1. Art und Fehler 2. Art
Da die Entscheidung über die Annahme oder Ablehnung der Nullhypothese aufgrund eines zufälligen Ergebnisses der Stichprobe erfolgt, kann es zu Fehlentscheidungen kommen.
Fehler 1. Art und Fehler 2. Art
Fehler 1. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich abgelehnt.
Fehler 2. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich angenommen bzw. nicht abgelehnt.
(vgl. Merkhilfe)
Die Wahrscheinlichkeit \(\alpha'\) für den Fehler 1. Art bzw. die Wahrscheinlichkeit \(\beta'\) für den Fehler 2. Art wird auch als Risiko 1. Art bzw. Risiko 2. Art bezeichnet.
Die folgende Tabelle gibt eine Übersicht zu den Entscheidungs- und Fehlermöglichkeiten bei einem Alternativtest.
| \(H_{0}\) ist wahr | \(H_{0}\) ist falsch | |
| \(H_{0}\) wird abgelehnt | Fehler 1. Art | Richtige Entscheidung |
| \(H_{0}\) wird angenommen | Richtige Entscheidung | Fehler 2. Art |
Wird bei festem Stichprobenumfang \(n\) der Annahmebereich \(A\) der Nullhypothese \(H_{0}\) vergrößert (verkleinert), so verkleinert (vergrößert) sich der Ablehnungsbereich \(\overline{A}\) der Nullhypothese. Das bedeutet, dass bei festem Stichprobenumfang \(n\) eine Verkleinerung des Fehlers 1. Art eine Vergrößerung des Fehlers 2. Art zur Folge hat und umgekehrt.
Eine Verringerung beider Fehler ist nur durch eine Erhöhung des Stichprobenumfangs \(n\) zu erreichen.
In den meisten Fällen wird darauf geachtet, dass die Wahrscheinlichkeit für den Fehler 1. Art gering ist. Zu diesem Zweck wird der Wahrscheinlichkeit für den Fehler 1. Art ein Obergrenze vorgegeben und unter dieser Bedingung eine Entscheidungsregel formuliert (vgl. Abiturskript - 3.4.2 Signifikanztest). Die Wahl der Nullhypothese ist somit keine Frage der Mathematik, sondern vielmehr eine Frage der Interessenperspektive. Die Nullhypothese wird so gewählt, dass der damit zu formulierende Fehler 1. Art den als am schwerwiegendsten erachteten Fehler beschreibt. Häufig soll entweder ein finanzieller Verlust oder ein Imageverlust durch eine geeignete Wahl der Nullhypothese und den damit verbundenen Fehler 1. Art begrenzt werden.
Lautet die Nullhypothese \(H_{0}\colon p \leq p_{0}\) oder \(H_{0}\colon p \geq p_{0}\), betrachtet man den „Extremfall" \(p = p_{0}\), um die maximale Wahrscheinlichkeit \(\alpha'\) für den Fehler 1. Art zu erfassen.
Die Wahrscheinlichkeit \(\beta'\) des Fehlers 2. Art kann nur berechnet werden, wenn bei einer Gegenhypothese \(H_{1}\colon p < p_{0}\) oder \(H_{1}\colon p > p_{0}\) eine konkrete Annahme für \(p_{1}\) getroffen wird.
Beispiel:
Betrachtet wird das Eintreten eines Ereignisses \(E\).
Die Zufallsgröße \(X\) gibt an, wie oft das Ereignis \(E\) bei der Stichprobe eintritt.
Stichprobenumfang: \(n = 10\)
\(p\): Trefferwahrscheinlichkeit für das Ereignis \(E\)
Die Zufallsgröße \(X\) ist nach \(B(10;p)\) binomialverteilt.
Nullhypothese \(H_{0}\colon p \leq 0{,}3\)
Gegenhypothese \(H_{1}\colon p > 0{,}3\)
Der Annahmebereich \(A\) und der Ablehnungsbereich \(\overline{A}\) sei wie folgt festgelegt:
Annahmebereich der Nullhypothese \(H_{0}\): \(A = \{0, \dots, 4\}\)
Ablehnungsbereich der Nullhypothese \(H_{0}\): \(\overline{A} = \{5, \dots, 10\}\)
Wahrscheinlichkeit \(\alpha'\) für den Fehler 1. Art
Die Nullhypothese \(H_{0}\colon p_{0}\leq 0{,}3\) ist wahr, wird aber abgelehnt, weil das Ergebnis der Stichprobe im Ablehnungsbereich \(\overline{A} = \{5, \dots, 10\}\) der Nullhypothese liegt. Für die Berechnung der maximalen Wahrscheinlichkeit \(\alpha'\) des Fehlers 1. Art wird der „Extremfall" \(p_{0} = 0{,}3\) betrachtet.
Unter Verwendung des Stochastischen Tafelwerks (ST) ergibt sich:
Ablehnungsbereich der Nullhypothese \(H_{0}\): \(\overline{A} = \{5, \dots, 10\}\)
\[\begin{align*}\alpha' &= P_{p_{0}}^{n} (X \in \overline{A}) \\[0.8em] &= P_{0{,}3}^{10}(X \geq 5) \\[0.8em] &= 1 - P_{0{,}3}^{10}(X \leq 4) \\[0.8em] &= 1 - \sum \limits_{i = 0}^{4}B(10;0{,}3;i) \\[0.8em] &\overset{\text{ST}}{=} 1 - 0{,}84973 \\[0.8em] &= 0{,}15027 \\[0.8em] &\approx 15{,}03\,\% \end{align*}\]
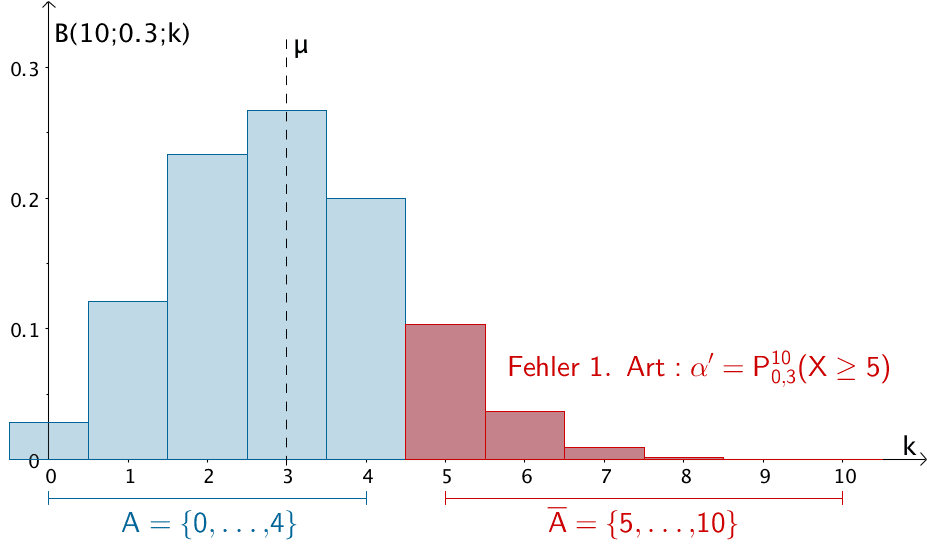
Maximale Wahrscheinlichkeit \(\alpha'\) für den Fehler 1. Art bei der Nullhypothese \(H_{0}\colon p \leq 0{,}3\) und der Betrachtung des „Extremfalls" \(p_{0} = 0{,}3\)
Wählt man für die Berechnung der Wahrscheinlichkeit \(\alpha'\) des Fehlers 1. Art bei der Nullhypothese \(H_{0}\colon p \leq 0{,}3\) nicht den „Extremfall" \(p_{0} = 0{,}3\), sondern beispielsweise \(p_{0} = 0{,}2\) erfasst man damit nicht die maximale Wahrscheinlichkeit für den Fehler 1. Art. Für \(p_{0} = 0{,}2\) ist das Maximum der Binomialverteilung der Zufallsgröße \(X\) hin zum Erwartungswert \(\mu = 2\) verschoben. Die Wahrscheinlichkeit \(\alpha' = P_{0{,}2}^{10}(X \geq 5)\) für den Fehler 1. Art ist dann kleiner als die maximale Wahrscheinlichkeit für den Fehler 1. Art \(\alpha' = P_{0{,}3}^{10}(X \geq 5)\).
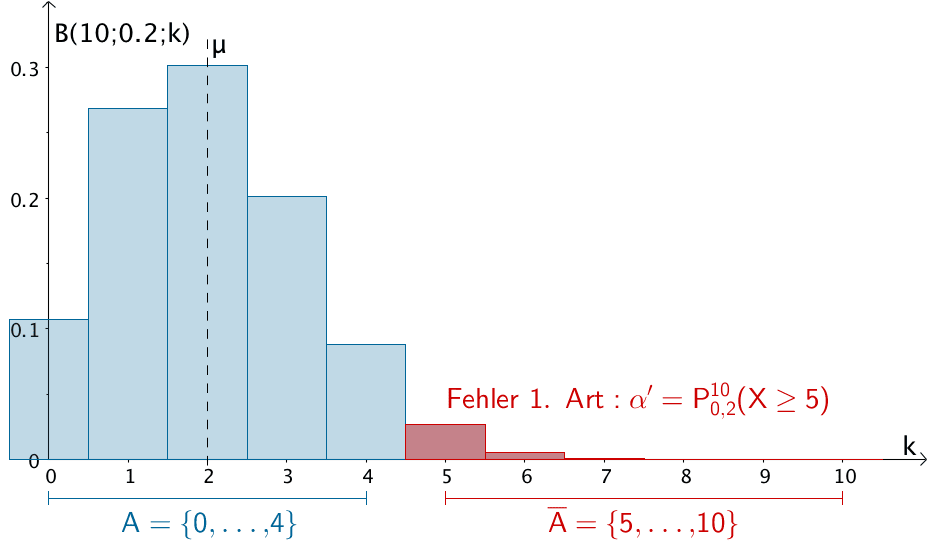
Wahrscheinlichkeit \(\alpha'\) für den Fehler 1. Art bei der Nullhypothese \(H_{0}\colon p \leq 0{,}3\) und der Betrachtung von \(p_{0} = 0{,}2\)
Wahrscheinlichkeit \(\beta'\) für den Fehler 2. Art
Die Nullhypothese \(H_{0}\colon p \leq 0{,}3\) ist falsch, wird aber angenommen, weil das Ergebnis der Stichprobe im Annahmebereich \(A = \{0, \dots, 4\}\) der Nullhypothese liegt. Um die Wahrscheinlichkeit \(\beta'\) für den Fehler 2. Art berechnen zu können, wird für die Gegenhypothese \(H_{1}\colon p > 0{,}3\) beispielsweise der konkreter Fall \(p_{1} = 0{,}5\) angenommen.
Unter Verwendung des Stochastischen Tafelwerks (ST) ergibt sich:
Annahmebereich der Nullhypothese \(H_{0}\): \(A = \{0, \dots, 4\}\)
\[\begin{align*}\beta' &= P_{p_{1}}^{n} (X \in A) \\[0.8em] &= P_{0{,}5}^{10}(X \leq 4) \\[0.8em] &= \sum \limits_{i = 0}^{4}B(10;0{,}5;i) \\[0.8em] &\overset{\text{ST}}{=} 0{,}37695 \\[0.8em] &\approx 37{,}70\,\% \end{align*}\]
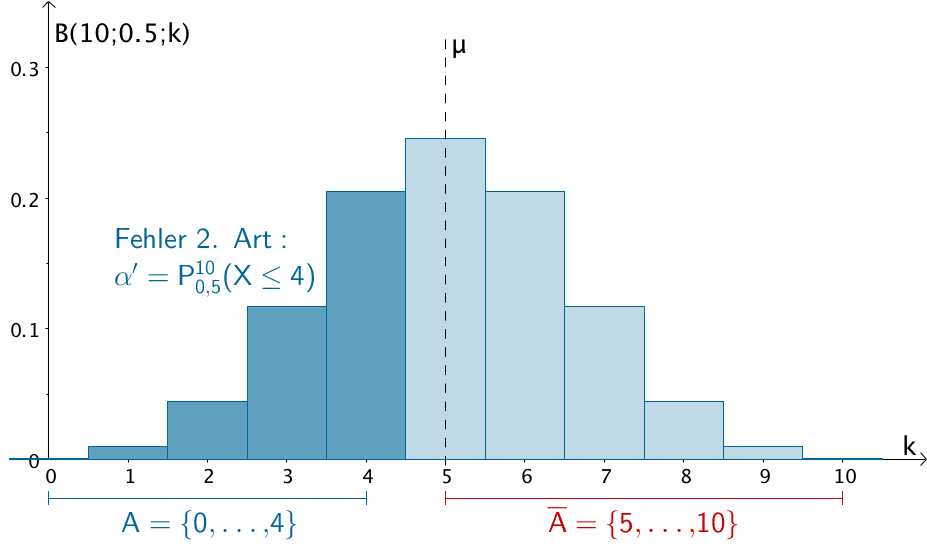
Wahrscheinlichkeit \(\beta'\) für den Fehler 2. Art unter der Annahme \(p_{1} = 0{,}5\)
Beispielaufgabe
Ein Pharmaunternehmen wirbt für ein neues Medikament und behauptet, dass mindestens 60 % der dafür infrage kommenden Patienten damit geheilt werden. Bei der Zulassung des Medikaments treten Zweifel an dessen Wirksamkeit auf. Deshalb wird an 50 freiwilligen Patienten ein Test vorgenommen. Man ist bereit, der Behauptung des Pharmaunternehmens zu vertrauen, wenn mindestens 27 der Testpatienten geheilt werden.
a) Beschreiben Sie für die Nullhypothese \(H_{0}\): „Mindestens 60 % der Patienten werden durch das neue Medikament geheilt" den Fehler 1. Art im Sachzusammenhang und berechnen Sie dessen Wahrscheinlichkeit. Berechnen Sie unter der Annahme der Gegenhypothese \(H_{1}\colon p_{1} = 0{,}4\) den Fehler 2. Art und beschreiben Sie diesen Im Sachzusammenhang.
b) Berechnen Sie jeweils die Wahrscheinlichkeit für den Fehler 1. Art und den Fehler 2. Art, wenn 100 freiwillige Patienten das Medikament testen und dessen Wirksamkeit durch mindestens 54 geheilte Patienten bestätigt wird. Vergleichen Sie die Ergebnisse aus den Teilaufgaben a) und b) und nehmen Sie dazu Stellung.
Teilaufgabe a
Zufallsgröße \(X\): „Anzahl der geheilten Testpatienten"
Stichprobenumfang: \(n = 50\) (Testpatienten)
\(p\): Trefferwahrscheinlichkeit dafür, dass ein Patient durch das Medikament geheilt wird.
Die Zufallsgröße \(X\) ist nach \(B(50;p)\) binomialverteilt.
Fehler 1. Art im Sachzusammenhang
Fehler 1. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich abgelehnt.
Nullhypothese \(H_{0}\): „Mindestens 60 % der Patienten werden durch das neue Medikament geheilt"
Annahmebereich der Nullhypothese \(H_{0}\): \(A = \{27, \dots, 50\}\)
Ablehnungsbereich der Nullhypothese \(H_{0}\): \(\overline{A} = \{0, 1, \dots, 26\}\)
Durch das neue Medikament können tatsächlich mindestens 60 % der Patienten geheilt werden. Das Medikament wird jedoch nicht zugelassen, weil (zufällig) höchstens 26 der Testpatienten geheilt werden.
Wahrscheinlichkeit \(\alpha'\) für den Fehler 1. Art
Fehler 1. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich abgelehnt.
Nullhypothese \(H_{0} \colon p \geq 0{,}6\)
Annahmebereich der Nullhypothese \(H_{0}\): \(A = \{27, \dots, 50\}\)
Ablehnungsbereich der Nullhypothese \(H_{0}\): \(\overline{A} = \{0, 1, \dots, 26\}\)
Um die maximale Wahrscheinlichkeit für den Fehler 1. Art zu erfassen, wird bei der Nullhypothese \(H_{0} \colon p \geq 0{,}6\) der „Extremfall" \(p_{0} = 0{,}6\) betrachtet.
Unter Verwendung des Stochastischen Tafelwerks (ST) ergibt sich:
\[\begin{align*} \alpha' &= P_{0{,}6}^{50}(X \in \overline{A}) \\[0.8em] &= P_{0{,}6}^{50}(X \leq 26) \\[0.8em] &\overset{\text{ST}}{=} 0{,}15617 \\[0.8em] &\approx 15{,}62\, \% \end{align*}\]
Wahrscheinlichkeit \(\alpha'\) für den Fehler 1. Art bei der Nullhypothese \(H_{0}\colon p \geq 0{,}6\)
Wahrscheinlichkeit \(\beta'\) für den Fehler 2. Art
Fehler 2. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich angenommen.
Nullhypothese \(H_{0} \colon p \geq 0{,}6\)
Gegenhypothese \(H_{1} \colon p < 0{,}6\), Annahme: \(p_{1} = 0{,}4\)
Annahmebereich der Nullhypothese \(H_{0}\): \(A = \{27, \dots, 50\}\)
Ablehnungsbereich der Nullhypothese \(H_{0}\): \(\overline{A} = \{0, 1, \dots, 26\}\)
Mit der Annahme \(p_{1} = 0{,}4\) lässt sich der Fehler 2. Art berechnen.
Unter Verwendung des Stochastischen Tafelwerks (ST) ergibt sich:
\[\begin{align*} \beta' &= P_{0{,}4}^{50}(X \in A) \\[0.8em] &= P_{0{,}4}^{50}(X \geq 27) \\[0.8em] &= 1 - P_{0{,}4}^{50}(X \leq 26) \\[0.8em] &\overset{\text{ST}}{=} 1 - 0{,}96859 \\[0.8em] &= 0{,}03141 \\[0.8em] &\approx 3{,}14\, \% \end{align*}\]
Wahrscheinlichkeit \(\beta'\) für den Fehler 2. Art unter der Annahme \(p_{1} = 0{,}4\)
Fehler 2. Art im Sachzusammenhang
Fehler 2. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich angenommen.
Nullhypothese \(H_{0} \colon p \geq 0{,}6\)
Gegenhypothese \(H_{1} \colon p < 0{,}6\), Annahme: \(p_{1} = 0{,}4\)
Annahmebereich der Nullhypothese \(H_{0}\): \(A = \{27, \dots, 50\}\)
Ablehnungsbereich der Nullhypothese \(H_{0}\): \(\overline{A} = \{0, 1, \dots, 26\}\)
Unter der Annahme, dass die Wirksamkeit des neuen Medikaments nur bei 40 % liegt, wird das Medikament dennoch zugelassen, wenn (zufällig) mindestens 27 der Testpatienten geheilt werden.
Teilaufgabe b
Zufallsgröße \(X\): „Anzahl der geheilten Testpatienten"
Stichprobenumfang: \(n = 100\) (Testpatienten)
\(p\): Trefferwahrscheinlichkeit dafür, dass ein Patient durch das Medikament geheilt wird.
Die Zufallsgröße \(X\) ist nach \(B(100;p)\) binomialverteilt.
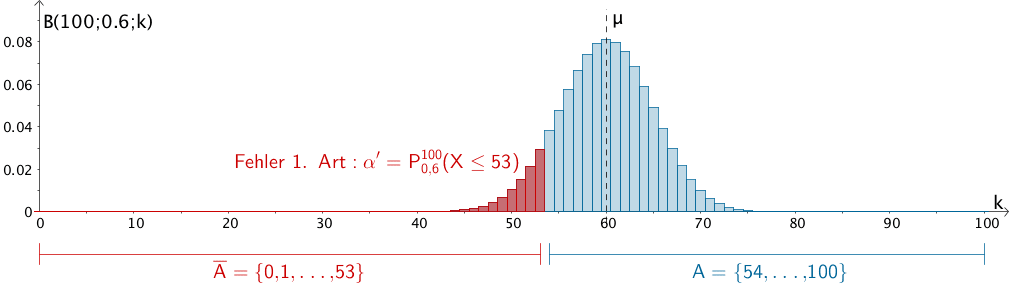
Wahrscheinlichkeit \(\alpha'\) für den Fehler 1. Art
Fehler 1. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich abgelehnt.
Nullhypothese \(H_{0} \colon p \geq 0{,}6\)
Annahmebereich der Nullhypothese \(H_{0}\): \(A = \{54, \dots, 100\}\)
Ablehnungsbereich der Nullhypothese \(H_{0}\): \(\overline{A} = \{0, 1, \dots, 53\}\)
Um die maximale Wahrscheinlichkeit für den Fehler 1. Art zu erfassen, wird bei der Nullhypothese \(H_{0} \colon p \geq 0{,}6\) der „Extremfall" \(p_{0} = 0{,}6\) betrachtet.
Unter Verwendung des Stochastischen Tafelwerks (ST) ergibt sich:
\[\begin{align*} \alpha' &= P_{0{,}6}^{100}(X \in \overline{A}) \\[0.8em] &= P_{0{,}6}^{100}(X \leq 53) \\[0.8em] &\overset{\text{ST}}{=} 0{,}09298 \\[0.8em] &\approx 9{,}30\, \% \end{align*}\]
Wahrscheinlichkeit \(\alpha'\) für den Fehler 1. Art mit der Nullhypothese \(H_{0}\colon p_{0} = 0{,}6\)
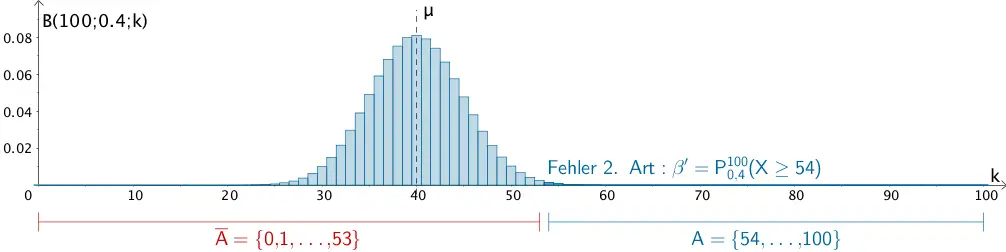
Wahrscheinlichkeit \(\beta'\) für den Fehler 2. Art
Fehler 2. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich angenommen.
Nullhypothese \(H_{0} \colon p \geq 0{,}6\)
Gegenhypothese \(H_{1} \colon p < 0{,}6\), Annahme: \(p_{1} = 0{,}4\)
Annahmebereich der Nullhypothese \(H_{0}\): \(A = \{54, \dots, 100\}\)
Ablehnungsbereich der Nullhypothese \(H_{0}\): \(\overline{A} = \{0, 1, \dots, 53\}\)
Mit der Annahme \(p_{1} = 0{,}4\) lässt sich der Fehler 2. Art berechnen.
Unter Verwendung des Stochastischen Tafelwerks (ST) ergibt sich:
\[\begin{align*} \beta' &= P_{0{,}4}^{100}(X \in A) \\[0.8em] &= P_{0{,}4}^{100}(X \geq 54) \\[0.8em] &= 1 - P_{0{,}4}^{100}(X \leq 53) \\[0.8em] &\overset{\text{ST}}{=} 1 - 0{,}99680 \\[0.8em] &= 0{,}00320 \\[0.8em] &\approx 0{,}32\, \% \end{align*}\]
Wahrscheinlichkeit \(\beta'\) für den Fehler 2. Art unter der Annahme \(p_{1} = 0{,}4\)
Vergleich der Ergebnisse aus den Teilaufgaben a und b
Ergebnisse aus Teilaufgabe a:
Stichprobenumfang: \(\boldsymbol{n = 50}\) (Testpatienten)
Nullhypothese \(H_{0} \colon p \geq 0{,}6\)
\(A = \{27, \dots, 50\}\)
\(\overline{A} = \{0, 1, \dots, 26\}\)
Fehler 1. Art: \(\alpha' \approx 15{,}62\, \%\)
Fehler 2. Art: \(\beta' \approx 3{,}14 \,\%\)
Ergebnisse aus Teilaufgabe b:
Stichprobenumfang: \(\boldsymbol{n = 100}\) (Testpatienten)
Nullhypothese \(H_{0} \colon p \geq 0{,}6\)
\(A = \{54, \dots, 100\}\)
\(\overline{A} = \{0, 1, \dots, 53\}\)
Fehler 1. Art: \(\alpha' \approx 9{,}30\,\%\)
Fehler 2. Art: \(\beta' \approx 0{,}32\,\%\)
Bewertung des Vergleichs:
Durch die Verdopplung des Stichprobenumfangs \(n\) von 50 auf 100 Testpatienten bei gleichzeitig proportionaler Anpassung des Annahmebereichs \(A\) bzw. des Ablehnungsbereichs \(\overline{A}\) der Nullhypothese \(H_{0}\) kann die Wahrscheinlichkeit des Fehlers 1. Art und des Fehler 2. Art verringert werden. Die Wahrscheinlichkeit \(\alpha'\) für den Fehler 1. Art nimmt von 15,62 % um 6,32 % auf 9,30 % ab. Die Wahrscheinlichkeit \(\beta'\) für den Fehler 2. Art nimmt von 3,14 % um 2,82 % auf 0,32 % ab.