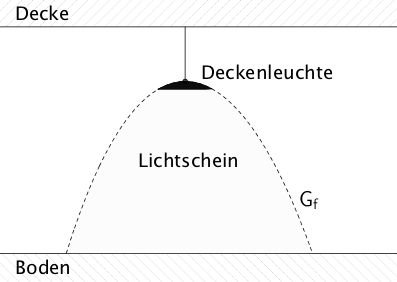
An der Decke eines Hausflurs ist eine Deckenleuchte angebracht. Die Randlinie des Lichtkegels der Deckenleuchte kann näherungsweise durch die Funktion \(\displaystyle f \colon x \mapsto -3 \cdot \left( e^{0{,}4x} + e^{-0{,}5x} \right) + 9\) beschrieben werden mit \(x\) und \(y\) in Metern (vgl. Abbildung). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Zeigen Sie, dass \(G_{f}\) nicht symmetrisch bezüglich des Koordinatensystems ist.
b) Ersetzen Sie einen Zahl \((\neq 0)\) des Funktionsterms \(f(x)\) so, dass \(G_{f}\) symmetrisch ist und geben Sie die Art der Symmetrie an.
Eine Feinjustierung der LEDs der Deckenleuchte verändert den Lichtkegel. Die Randlinie des veränderten Lichtkegels wird nun näherungsweise durch die Funktion \(g \colon x \mapsto -3 \cdot \left( e^{0{,}5x} + e^{-0{,}5x} \right) + 9\) beschrieben. Der Graph der Funktion \(g\) wird mit \(G_{g}\) bezeichnet.
c) Bestimmen Sie die Schnittpunkte von \(G_{g}\) mit den Koordinatenachsen. Hinweis: Verwenden Sie die Substitution \(u = e^{0{,}5x}\) zur Bestimmung der Schnittpunkte mit der \(x\)-Achse.
d) Berechnen Sie den Winkel, unter dem \(G_{g}\) die negative \(x\)-Achse schneidet.
e) Die Position der Aufhängung der Deckenleuchte entspricht der Lage des Hochpunkts von \(G_{g}\). Die Aufhängung ist 85 cm von der Decke entfernt. Berechnen Sie die Raumhöhe \(h\) des Hausflurs, an dessen Decke die Deckenleuchte angebracht ist.
a) Nachweis, dass \(G_{f}\) nicht symmetrisch bezüglich des Koordinatensystems ist
Man bestimmt den Funktionsterm \(f(-x)\). Gilt \(f(-x) = f(x)\), ist \(G_{f}\) achsensymmetrisch zur \(y\)-Achse. Gilt \(f(-x) = -f(x)\), ist \(G_{f}\) punktsymmetrisch zum Koordinatenursprung \(O(0|0)\). Trifft keiner der beiden Fälle zu, weist \(G_{f}\) keines der beiden Symmetrieverhalten auf.
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
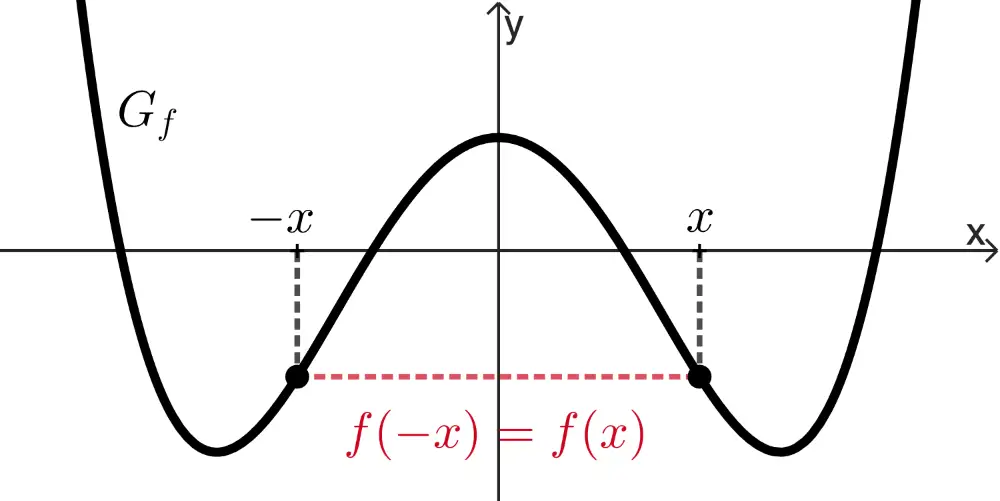
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
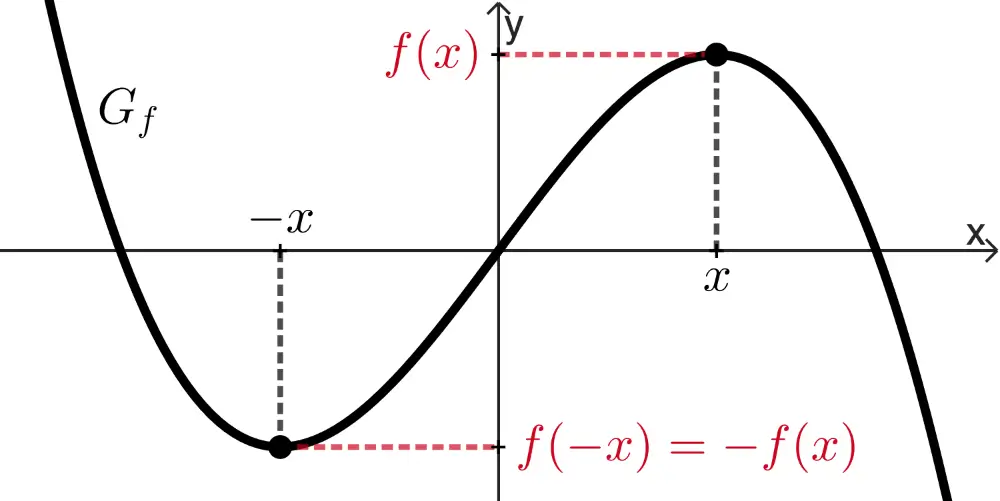
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[f(x) = -3 \cdot \left( e^{0{,}4x} + e^{-0{,}5x} \right) + 9\]
\[\begin{align*}f(-x) &= -3 \cdot \left( e^{0{,}4 \cdot (-x)} + e^{-0{,}5 \cdot (-x)} \right) + 9 \\[0.8em] &= -3 \cdot \left( e^{-0{,}4x} + e^{0{,}5x} \right) + 9 \end{align*}\]
\[\Longrightarrow \quad f(-x) \neq f(x); \; f(-x) \neq -f(x)\]
\(\Longrightarrow \quad G_{f}\) ist nicht symmetrisch bezüglich des Koordinatensystems.
b) Ersetzen einer Zahl von \(f(x)\), sodass \(G_{f}\) symmetrisch ist und Art der Symmetrie
Anmerkung:
Es ist lediglich eine Zahl von \(f(x)\) zu ersetzen und die Art der Symmetrie anzugeben. Jede Erklärung oder Rechnung kann entfallen.
\[f(x) = -3 \cdot \left( e^{0{,}4x} + e^{-0{,}5x} \right) + 9\]
Wenn sich die Exponenten der Exponentialterme \(e^{0{,}4x}\) und \(e^{-0{,}5x}\) nur durch das Vorzeichen unterscheiden, bleibt die Summe der Exponentialterme für \(-x\) erhalten. Man ersetzt entweder den Faktor \(0{,}4\) des einen Exponenten durch die Zahl \(0{,}5\) oder den Faktor \(-0{,}5\) des anderen Exponenten durch die Zahl \(-0{,}4\).
Es ergeben sich somit folgende Funktionen \(f_{1}\) und \(f_{2}\):
\[f_{1}(x) = -3 \cdot \left( e^{0{,}5x} + e^{-0{,}5x} \right) + 9\]
\[f_{2}(x) = -3 \cdot \left( e^{0{,}4x} + e^{-0{,}4x} \right) + 9\]
Die Graphen der Funktionen \(f_{1}\) und \(f_{2}\) sind achsensymmetrisch bezüglich der \(y\)-Achse, denn es gilt:
\[\begin{align*}f_{1}(-x) &= -3 \cdot \left( e^{0{,}5 \cdot (-x)} + e^{-0{,}5 \cdot (-x)} \right) + 9 \\[0.8em] &= -3 \cdot \left( e^{-0{,}5x} + e^{0{,}5x} \right) + 9 \\[0.8em] &= -3 \cdot \left( e^{0{,}5x} + e^{-0{,}5x} \right) + 9 \\[0.8em] &= f_{1}(x) \end{align*}\]
und
\[\begin{align*}f_{2}(-x) &= -3 \cdot \left( e^{0{,}4 \cdot (-x)} + e^{-0{,}4 \cdot (-x)} \right) + 9 \\[0.8em] &= -3 \cdot \left( e^{-0{,}4x} + e^{0{,}4x} \right) + 9 \\[0.8em] &= -3 \cdot \left( e^{0{,}4x} + e^{-0{,}4x} \right) + 9 \\[0.8em] &= f_{2}(x) \end{align*}\]
c) Schnittpunkte von \(G_{g}\) mit den Koordinatenachsen
\[g(x) = -3 \cdot \left( e^{0{,}5x} + e^{-0{,}5x} \right) + 9\]
Schnittpunkt(e) von \(G_{g}\) mit der \(x\)-Achse (Nullstelle(n))
Der Ansatz \(g(x) = 0\) ergibt eine Exponentialgleichung. Die Aufgabenstellung weist darauf hin, die Exponentialgleichung mithilfe der Substitution \(u = e^{0{,}5x}\) zu lösen. Vorab der Substitution erfolgen zweckmäßig einige elementare Umformungen.
\[\begin{align*}g(x) &= 0 \\[0.8em] -3 \cdot \left( e^{0{,}5x} + e^{-0{,}5x} \right) + 9 &= 0 & &| : (-3) \\[0.8em] e^{0{,}5x} + e^{-0{,}5x} - 3 &= 0 & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] e^{0{,}5x} + \frac{1}{e^{0{,}5x}} - 3 &= 0 & &| \cdot e^{0{,}5x} \\[0.8em] \left( e^{0{,}5x} \right)^{2} + 1 -3e^{0{,}5x} &= 0 \\[0.8em] \left( e^{0{,}5x} \right)^{2} -3e^{0{,}5x} + 1 &= 0 & &| \; \text{Substitution:} \; u = e^{0{,}5x} \\[0.8em] u^{2} - 3u + 1 &= 0 \end{align*}\]
Durch die Substitution \(u = e^{0{,}5x}\) wird die Exponentialgleichung in eine quadratische Gleichung übergeführt, welche sich mithilfe der Lösungsformel für quadratische Gleichungen lösen lässt. Da die Substitution keine Äquivalenzumformung ist, können Scheinlösungen auftreten. Mit \(e^{0{,}5x} > 0\) sind nur positive Werte für \(u\) erlaubt.
\[u^{2} -3u + 1 = 0; \; u > 0\]
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*} u_{1,2} &= \frac{3 \pm \sqrt{(-3)^{2} - 4 \cdot 1 \cdot 1}}{2 \cdot 1} \\[0.8em] &= \frac{3 \pm \sqrt{5}}{2} \end{align*}\]
\[u_{1} = \frac{3 + \sqrt{5}}{2} \approx 2{,}62\]
\[u_{2} = \frac{3 - \sqrt{5}}{2} \approx 0{,}38\]
Beide Lösungen \(u_{1}\) und \(u_{2}\) sind positiv und kommen somit für die Rücksubstitution \(e^{0{,}5x} = u\) in Frage.
Rücksubstitution:
Für die Rücksubstitution werden die exakten Werte von \(u_{1}\) und \(u_{2}\) (Wuzelterme) verwendet, um unnötige Rundungsfehler zu vermeiden.
\[\begin{align*}e^{0{,}5x} &= u_{1} \\[0.8em] e^{0{,}5x} &= \frac{3 + \sqrt{5}}{2} & &| \; \ln \; \text{(Logarithmieren)} \\[0.8em] \ln\left( e^{0{,}5x} \right) &= \ln\left( \frac{3 + \sqrt{5}}{2} \right) & &| \; \ln{e^{x}} = x \; \left( \text{allg.:}\; \log_{a}{a^{x}} = x \right) \\[0.8em] 0{,}5x &= \ln\left( \frac{3 + \sqrt{5}}{2} \right) & &| \cdot 2 \\[0.8em] x &= 2 \ln\left( \frac{3 + \sqrt{5}}{2} \right) \\[0.8em] &\approx 1{,}92 \end{align*}\]
\[\begin{align*}e^{0{,}5x} &= u_{2} \\[0.8em] e^{0{,}5x} &= \frac{3 - \sqrt{5}}{2} & &| \; \ln \; \text{(Logarithmieren)} \\[0.8em] \ln\left( e^{0{,}5x} \right) &= \ln\left( \frac{3 - \sqrt{5}}{2} \right) & &| \; \ln{e^{x}} = x \; \left( \text{allg.:}\; \log_{a}{a^{x}} = x \right) \\[0.8em] 0{,}5x &= \ln\left( \frac{3 - \sqrt{5}}{2} \right) & &| \cdot 2 \\[0.8em] x &= 2 \ln\left( \frac{3 - \sqrt{5}}{2} \right) \\[0.8em] &\approx -1{,}92 \end{align*}\]
Der Graph \(G_{g}\) schneidet die \(x\)-Achse in den Punkten \(N_{1}\Big( 2\ln\left( \frac{3 + \sqrt{5}}{2} \right) \Big| 0\Big)\) und \(N_{2}\Big( 2\ln\left( \frac{3 - \sqrt{5}}{2} \right) \Big| 0\Big)\).
Anmerkung:
Die Funktion \(g\) entspricht einer der Lösungen zu Teilaufgabe b. In Kenntnis der Achsensymmetrie von \(G_{g}\) bezüglich der \(y\)-Achse lässt sich eine der Rücksubstitutionen vermeiden, wenn man die Lage der jeweils zweiten Nullstelle durch die Symmetrie begründet.
Schnittpunkt von \(g_{g}\) mit der \(y\)-Achse
Der Graph \(G_{g}\) schneidet die \(y\)-Achse im Punkt \(S_{y}(0|g(0))\). Es ist also der Funktionswert \(g(0)\) zu berechnen.
\[g(x) = -3 \cdot \left( e^{0{,}5x} + e^{-0{,}5x} \right) + 9\]
\[\begin{align*}g(0) &= -3 \cdot \left( e^{0{,}5 \cdot 0} + e^{-0{,}5 \cdot 0} \right) + 9 \\[0.8em] &= -3 \cdot \left( e^{0} + e^{0} \right) + 9 \\[0.8em] &= -3 \cdot (1 + 1) + 9 \\[0.8em] &= 3 \end{align*}\]
\(\Longrightarrow \quad G_{g}\) schneidet die \(y\)-Achse im Punkt \(S_{y}(0|3)\).
d) Winkel, unter dem \(G_{g}\) die negative \(x\)-Achse schneidet
Der Graph der Funktion \(g\) schneidet die negative \(x\)-Achse im Punkt \(N_{2}\Big( 2\ln\left( \frac{3 - \sqrt{5}}{2} \right) \Big| 0\Big)\) (vgl. Teilaufgabe c).
Der Schnittwinkel von \(G_{g}\) mit der negativen \(x\)-Achse ist gleich dem spitzen Winkel, den die Tangente an \(G_{g}\) im Punkt \(N_{2}\) mit der \(x\)-Achse einschließt. Im Falle einer positiven Tangentensteigung entspricht der Schnittwinkel dem Steigungswinkel der Tangente.
Für den Steigungswinkel \(\alpha\) einer Geraden mit der Steigung \(m\) gilt:
Steigungswinkel \(\alpha\) einer Gerade \(g \colon y = m \cdot x +t\)
\[\tan \alpha = m \qquad \alpha \neq 90^\circ\]
\[\tan{\alpha} = m\]
Für den Steigungswinkel \(\alpha\) der Tangente \(T\) an \(G_{g}\) im Punkt \(N_{2}\) gilt folglich:
\[\tan{\alpha} = m_{T}\]
Die erste Ableitung \(g'\) an der Stelle \(x = 2\ln\left( \frac{3 - \sqrt{5}}{2} \right)\) berechnet die Steigung \(m_{T}\) der Tangente \(T\) an \(G_{g}\) im Punkt \(N_{2}\Big( 2\ln\left( \frac{3 - \sqrt{5}}{2} \right) \Big| 0\Big)\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[m_{T} = g'\Big( \textstyle 2\ln\left( \frac{3 - \sqrt{5}}{2} \right) \Big)\]
Mit \(\tan{\alpha} = m_{T}\) folgt:
\[\tan{\alpha} = g'\Big( \textstyle 2\ln\left( \frac{3 - \sqrt{5}}{2} \right) \Big)\]
Erste Ableitung \(g'\) bilden:
Die Funktion \(g\) wird mithilfe der Ableitung der natürlichen Exponentialfunktion, der Kettenregel, der Ableitung einer Potenzfunktion sowie der Summen- und der Faktorregel abgeleitet.
\[g(x) = -3 \cdot \left( e^{0{,}5x} + e^{-0{,}5x} \right) + 9\]
Ableitung der natürlichen Exponentialfunktion
\[f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
(vgl. Merkhilfe)
\[\begin{align*} g'(x) &= -3 \cdot \left( e^{0{,}5x} \cdot 0{,}5 + e^{-0{,}5x} \cdot (-0{,}5) \right) + 0 \\[0.8em] &= -3 \cdot \left( 0{,}5e^{0{,}5x} - 0{,}5e^{-0{,}5x} \right) \\[0.8em] &= (-3) \cdot 0{,}5 \cdot \left( e^{0{,}5x} - e^{-0{,}5x} \right) \\[0.8em] &= -1{,}5 \cdot \left( e^{0{,}5x} - e^{-0{,}5x} \right) \end{align*}\]
Steigungswinkel \(\alpha\) der Tangente \(T\) an \(G_{g}\) im Punkt \(N_{2}\) berechnen:
\[g'(x) = -1{,}5 \cdot \left( e^{0{,}5x} - e^{-0{,}5x} \right)\]
\(N_{2}\Big( 2\ln\left( \frac{3 - \sqrt{5}}{2} \right) \Big| 0\Big)\)
\[\begin{align*} \tan{\alpha} &= g'\Big( \textstyle 2\ln\left( \frac{3 - \sqrt{5}}{2} \right) \Big) \\[0.8em] &= -1{,}5 \cdot \left( e^{0{,}5 \cdot 2\ln\left( \frac{3 - \sqrt{5}}{2} \right)} - e^{(-0{,}5) \cdot 2\ln\left( \frac{3 - \sqrt{5}}{2} \right)} \right) \\[0.8em] &= -1{,}5 \cdot \left( e^{\ln\left( \frac{3 - \sqrt{5}}{2} \right)} - e^{-\ln\left( \frac{3 - \sqrt{5}}{2} \right)} \right) & &| \; \log_{a}{b^{n}} = n \cdot \log_{a}{b} \\[0.8em] &= -1{,}5 \cdot \left( e^{\ln\left( \frac{3 - \sqrt{5}}{2} \right)} - e^{\ln\left( \left(\frac{3 - \sqrt{5}}{2}\right)^{-1} \right)} \right) \\[0.8em] &= -1{,}5 \cdot \left( e^{\ln\left( \frac{3 - \sqrt{5}}{2} \right)} - e^{\ln\left( \frac{2}{3 - \sqrt{5}} \right)} \right) & &| \ln{e^{x}} = x \; \left( \text{allg.:} \; \log_{a}{a^{x}} = x \right) \\[0.8em] &= -1{,}5 \cdot \left( \frac{3-\sqrt{5}}{2} - \frac{2}{3 - \sqrt{5}} \right) \\[0.8em] &= -1{,}5 \cdot \frac{(3 - \sqrt{5})^{2} - 2 \cdot 2}{2 \cdot (3 - \sqrt{5})} \\[0.8em] &= -1{,}5 \cdot \frac{9 - 6\sqrt{5} + 5 - 4}{2 \cdot (3 - \sqrt{5})} \\[0.8em] &= -1{,}5 \cdot \frac{10 - 6\sqrt{5}}{2 \cdot (3 - \sqrt{5}} \\[0.8em] &= \frac{-15 + 9\sqrt{5}}{2 \cdot (3 - \sqrt{5})} \\[0.8em] &= \frac{(-15 + 9\sqrt{5}) \cdot (3 + \sqrt{5})}{2 \cdot (3 - \sqrt{5}) \cdot (3 + \sqrt{5})} & &| \; \text{Erweitern, 3. Binom. Formel anwenden} \\[0.8em] &= \frac{-45 + 27\sqrt{5} + 45 - 15\sqrt{5}}{2 \cdot (9 - 5)} \\[0.8em] &= \frac{12\sqrt{5}}{8} \\[0.8em] &= \frac{3\sqrt{5}}{2} & &| \; \text{TR:} \; \tan^{-1}(\dots) \\[3.2em] \alpha &\approx 73{,}40^{\circ} \end{align*}\]
Der Graph \(G_{g}\) schneidet die negative \(x\)-Achse unter einem Winkel von ca. 73,40°.
e) Raumhöhe des Hausflurs, an dessen Decke die Deckenleuchte angebracht ist
Die Position der Aufhängung der Deckenleuchte entspricht der Lage des Hochpunkts \(HoP(x_{0}|g(x_{0}))\) von \(G_{g}\). Die Aufhängung ist 85 cm von der Decke entfernt. Eine Längeneinheit entspricht einem Meter (vgl. Angabe).
Damit ergibt sich die Raumhöhe \(h\) zu:
\[h = g(x_{0}) + 0{,}85\]
Lage der Stelle \(x_{0}\) des Hochpunkts von \(G_{g}\):
Die Nullstellen der Funktion \(g\) liegen symmetrisch bezüglich der \(y\)-Achse (vgl. Teilaufgabe c). Der Verlauf des Graphen \(G_{g}\) ist ähnlich dem Verlauf des in der Abbildung der Angabe gezeigten Graphen \(G_{f}\) mit dem Unterschied, dass \(G_{g}\) symmetrisch bezüglich der \(y\)-Achse verläuft. Daraus lässt sich schlussfolgern, dass der Hochpunkt von \(G_{g}\) an der Stelle \(x_{0} = 0\) liegt.
Rechnerische Bestimmung der Koordinaten des Hochpunkts \(HoP(x_{0}|g(x_{0}))\) von \(G_{g}\):
An der Stelle \(x_{0}\) besitzt der Graph der Funktion \(g\) eine waagrechte Tangente, das heißt, die Tangentensteigung ist gleich Null. Die erste Ableitung \(g'\) der Funktion \(g\) beschreibt die Steigung einer Tangente an den Graphen der Funktion \(g\),
Folglich lautet die notwendige Bedingung für einen Hochpunkt von \(G_{g}\):
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[g'(x) = 0\]
Die erste Ableitung \(g'\) ist bereits aus Teilaufgabe d bekannt:
\[g'(x) = -1{,}5 \cdot \left( e^{0{,}5x} - e^{-0{,}5x} \right)\]
Nullstelle von \(g'\) berechnen:
\[\begin{align*}g'(x) = 0 \\[0.8em] -1{,}5 \cdot \left( e^{0{,}5x} - e^{-0{,}5x} \right) &= 0 \\[3.2em] \Longrightarrow \quad e^{0{,}5x} - e^{-0{,}5x} &= 0 & &| + e^{-0{,}5x} \\[0.8em] e^{0{,}5x} &= e^{-0{,}5x} & &| \; \ln \; \text{(Logarithmieren)} \\[0.8em] \ln\left( e^{0{,}5x} \right) &= \ln\left( e^{-0{,}5x} \right) & &| \; \ln{e^{x}} = x \; \left( \text{allg.:}\; \log_{a}{a^{x}} = x \right) \\[0.8em] 0{,}5x &= -0{,}5x & &| + 0{,}5x \\[0.8em] x &= 0 \end{align*}\]
Oder in Kurzschreibweise:
\[\begin{align*} \Longrightarrow \quad e^{0{,}5x} - e^{-0{,}5x} &= 0 & &| + e^{-0{,}5x} \\[0.8em] e^{0{,}5x} &= e^{-0{,}5x} & &| \; \text{Exponentenvergleich} \\[0.8em] 0{,}5x &= -0{,}5x & &| + 0{,}5x \\[0.8em] x &= 0 \end{align*}\]
An der Stelle \(x_{0} = 0\) besitzt \(G_{g}\) eine waagrechte Tangente, welche auf einen Extrempunkt (bzw. einen Terrassenpunkt) von \(G_{g}\) hinweist.
Nachweis der Art des Extrempunkts:
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[g'(x) = -1{,}5 \cdot \left( e^{0{,}5x} - e^{-0{,}5x} \right)\]
Der Term \(\left( e^{0{,}5x} - e^{-0{,}5x} \right)\) bestimmt den Vorzeichenwechsel von \(g'\) in der Umgebung der Stelle \(x_{0} = 0\). Der Vorzeichenwechsel lässt sich besser beurteilen und dokumentieren, wenn man den Term mithilfe der Rechenregel für Potenzen \(a^{-n} = \frac{1}{a^{n}}; \; a \in \mathbb R \backslash \{0\}, \; n \in \mathbb N\) umformt.
\[\left(e^{0{,}5x} - e^{-0{,}5x}\right) = \left(e^{0{,}5x} - \frac{1}{e^{0{,}5x}}\right)\]
Es git: \(e^{0{,}5x} < 1\) für \(x < 0\) und \(e^{0{,}5x} > 1\) für \(x > 0\).
Daraus folgt:
\(\left(e^{0{,}5x} - \dfrac{1}{e^{0{,}5x}}\right) < 0\) für \(x < 0\)
\(\left(e^{0{,}5x} - \dfrac{1}{e^{0{,}5x}}\right) > 0\) für \(x > 0\)
Somit ergibt sich:
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[\left. \begin{align*} &g'(x) > 0 \; \text{für} \; x < 0 \\[0.8em] &g'(0) = 0 \\[0.8em] &g'(x) < 0 \; \text{für} \; x > 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkt}\; HoP(0|g(0))\]
Veranschaulichung mit einer Monotonietabelle:
\[g'(x) = -1{,}5 \cdot \left( e^{0{,}5x} - e^{-0{,}5x} \right) = -1{,}5 \cdot \left( e^{0{,}5x} - \frac{1}{e^{0{,}5x}} \right)\]
| \(x\) | \(x < 0\) | \(x = 0\) | \(x > 0\) |
| \(-1{,}5\) | \(-\) | \(-\) | \(-\) |
| \(\left( e^{0{,}5x} - \dfrac{1}{e^{0{,}5x}} \right)\) | \(-\) | \(0\) | \(+\) |
| \(g'(x)\) | \(+\) | \(0\) | \(-\) |
| \(G_{g}\) | \(\nearrow\) | Hochpunkt \(HoP(0|g(0))\) | \(\searrow\) |
\(y\)-Koordinate des Hochpunkts berechnen:
\[g(x) = -3 \cdot \left( e^{0{,}5x} + e^{-0{,}5x} \right) + 9\]
\[g(0) = -3 \cdot \left( e^{0{,}5 \cdot 0} + e^{-0{,}5 \cdot 0} \right) + 9 = -3 \cdot (1 + 1) + 9 = 3\]
\[\Longrightarrow \quad HoP(0|3)\]
Raumhöhe \(h\) berechnen:
\[h = g(0) + 0{,}85 = 3 + 0{,}85 = 3{,}85\]
Die Raumhöhe des Hausflurs, an dessen Decke die Deckenleuchte angebracht ist, beträgt 3,85 m.

