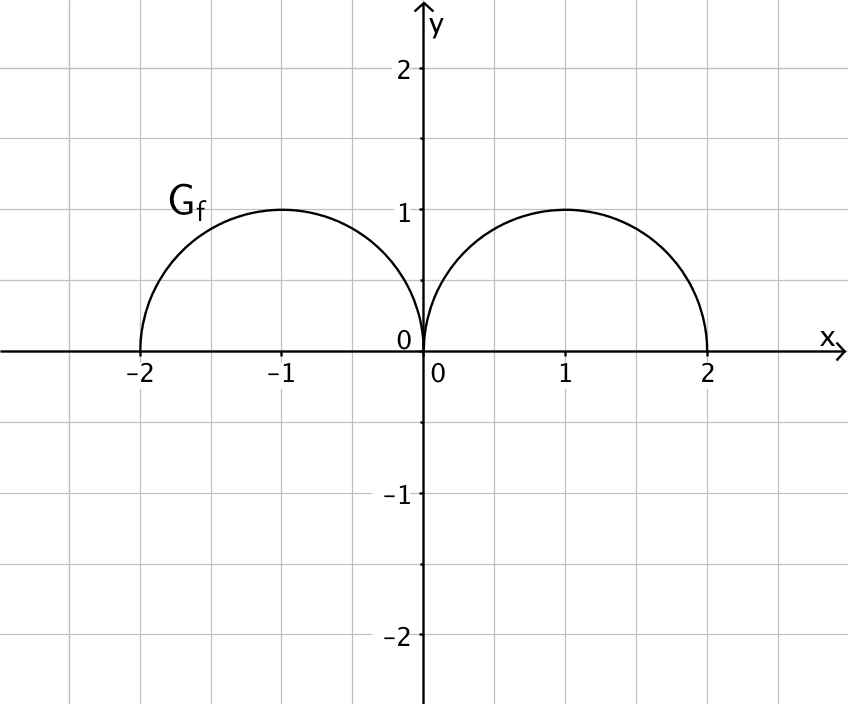
 Abb. 1
Abb. 1Abbildung 1 zeigt den Graphen \(G_f\) der Funktion \(f\) mit Definitionsbereich \([-2;2]\). Der Graph besteht aus zwei Halbkreisen, die die Mittelpunkte \((-1|0)\) bzw. \((1|0)\) sowie jeweils den Radius 1 besitzen. Betrachtet wird die in \([-2;2]\) definierte Integralfunktion \(\displaystyle F \colon \mapsto \int_0^x f(t)\,dt\).
Geben Sie \(F(0)\), \(F(2)\) und \(F(-2)\) an.
(3 BE)
Lösung zu Teilaufgabe 4a
\[F(x) = \int_0^x f(t)\,dt\,; \quad D = [-2;2]\]
Nullstelle einer Integralfunktion
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) besitzt an der unteren Integrationsgrenze \(x = a\) eine Nullstelle.
\[I_{a}(a) = \int_{a}^{a} f(t) \, dt = F(a) - F(a) = 0\]
\(F\) ist eine Stammfunktion von \(f\).
\[F(0) = \int_0^0 f(t)\,dt = 0\]
\[F(2) = \int_0^2 f(t)\,dt \]
Der Wert des bestimmten Integrals \(\displaystyle \int_0^2 f(t)\,dt\) ist gleich der Maßzahl des Flächeninhalts \(A\) des Halbkreises mit dem Mittelpunkt \((1|0)\) und dem Radius 1.
\[A_{\text{Halbkreis}} = \frac{1}{2}r^{2}\pi\]
\[F(2) = \int_0^2 f(t)\,dt = \frac{1}{2} \cdot 1^2 \cdot \pi = \frac{\pi}{2}\]
\[F(-2) = \int_0^{-2} f(t)\,dt = - \int_{-2}^0 f(t)\,dt = -\frac{\pi}{2}\]
Das bestimmte Integral \(\displaystyle \int_0^{-2} f(t)\,dt\) zählt den Flächeninhalt \(A\) negativ, da „nach links" integriert wird.
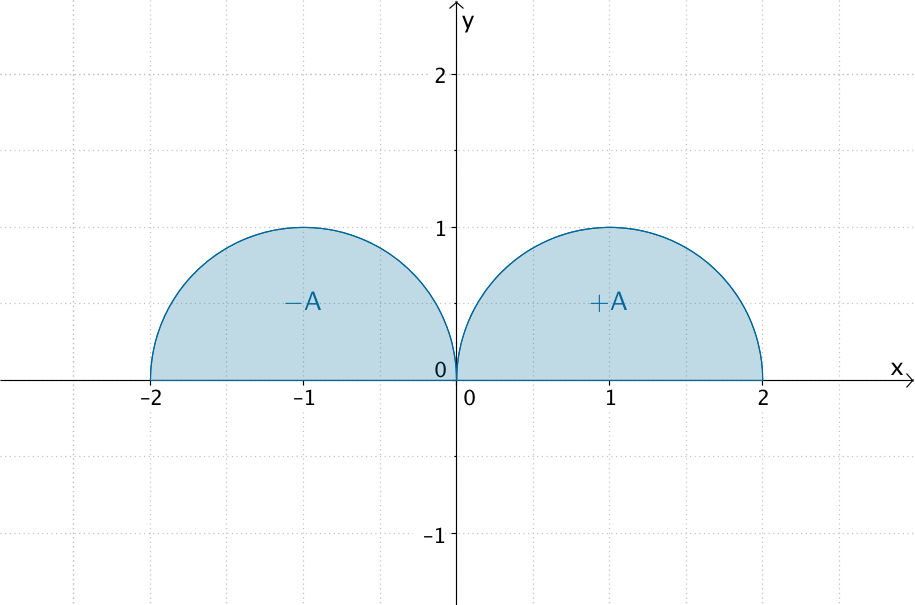
\(\displaystyle F(-2) = \int_0^{-2} f(t)\,dt = -A\,;\) \(\displaystyle F(2) = \int_0^2 f(t)\,dt = A\)


