In einem kartesischen Koordinatensystem sind die Punkte \(A\,(10|2|0)\), \(B\,(10|8|0)\), \(C\,(10|4|3)\), \(R\,(2|2|0)\), \(S\,(2|8|0)\) und \(T\,(2|4|3)\) gegeben. Der Körper \(ABCRST\) ist ein gerades dreiseitiges Prisma mit der Grungfläche \(ABC\), der Deckfläche \(RST\) und rechteckigen Seitenflächen.
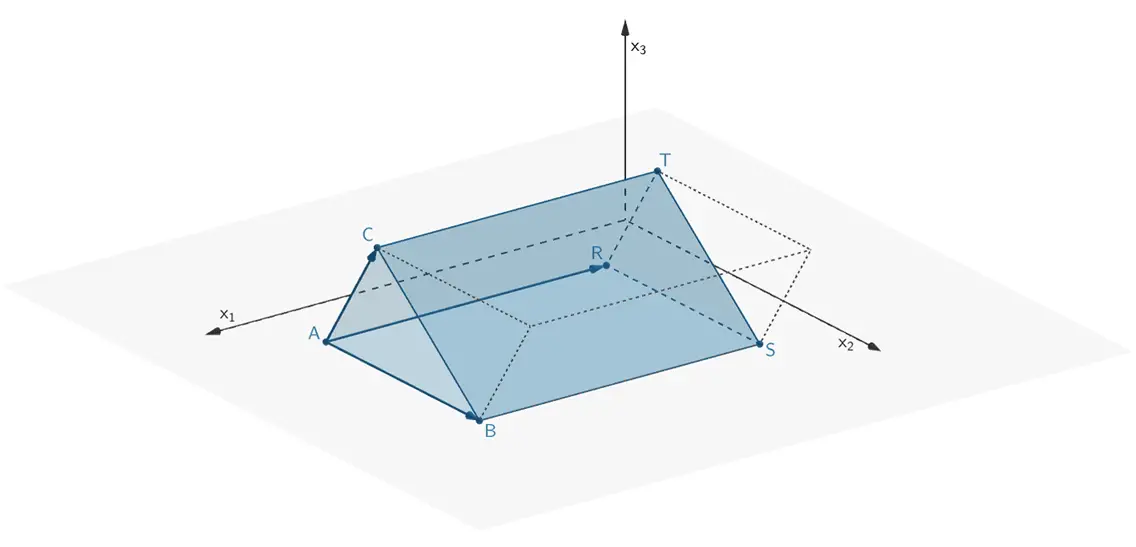
Zeichen Sie das Prisma in ein kartesisches Koordinatensystem (vgl. Abbildung) ein. Welche besondere Lage im Koordinatensystem hat die Grundfläche \(ABC\,\)? Berechnen Sie das Volumen des Prismas.
(6 BE)
Lösung zu Teilaufgabe a
Zeichnung des Prismas \(ABCRST\)
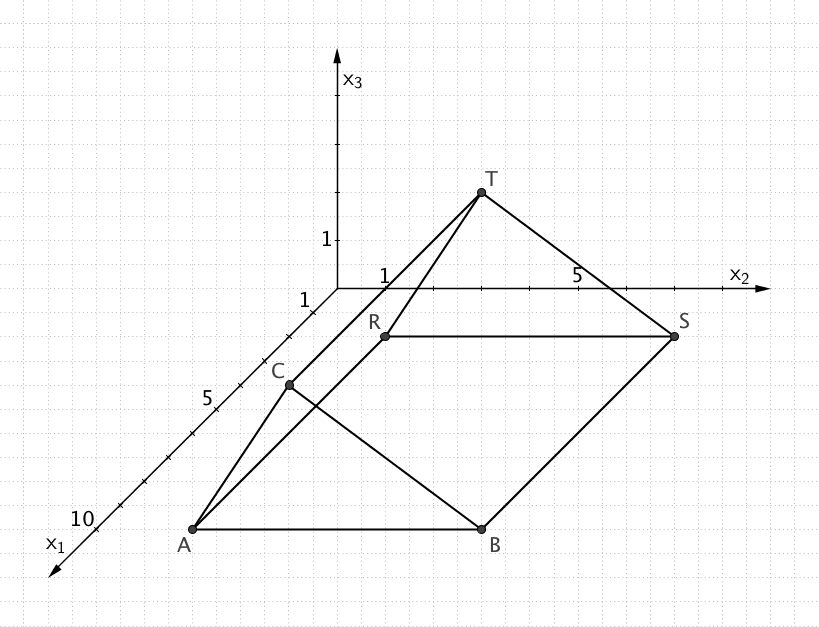
Gerades dreiseitiges Prisma \(ABCRST\) mit der Grundfläche \(ABC\)
\(A\,(10|2|0)\,\), \(B\,(10|8|0)\,\), \(C\,(10|4|3)\,\), \(R\,(2|2|0)\,\), \(S\,(2|8|0)\,\), \(T\,(2|4|3)\)
Besondere Lage der Grundfläche \(ABC\)
Lagebeziehung von Ebenen
|
\(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace\) und \(\enspace F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{B}) = 0\) oder \(E \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} + \mu \cdot \overrightarrow{v}; \; \lambda, \mu \in \mathbb R \enspace\) und \(\enspace F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{B}) = 0\)
|
|||
|
\(\overrightarrow{n}_{E} = k \cdot \overrightarrow{n}_{F}, \; k \in \mathbb R\) \(\Rightarrow \; \overrightarrow{n}_{E} \parallel \overrightarrow{n}_{F}\) oder \(\overrightarrow{u} \circ \overrightarrow{n}_{F} = 0\) und \(\overrightarrow{v} \circ \overrightarrow{n}_{F} = 0\) \(\Leftrightarrow \; \overrightarrow{u} \perp \overrightarrow{n}_{F}\) und \(\overrightarrow{v} \perp \overrightarrow{n}_{F}\)
|
\(\overrightarrow{n}_{E} \neq k \cdot \overrightarrow{n}_{F}, \; k \in \mathbb R\) \(\Rightarrow \; \overrightarrow{n}_{E}\nparallel \overrightarrow{n}_{F}\) oder \(\overrightarrow{u} \circ \overrightarrow{n}_{F} \neq 0\) und/oder \(\overrightarrow{v} \circ \overrightarrow{n}_{F} \neq 0 \)
|
||
|
\(B \in E\) oder \(A \in F\) \(\Longrightarrow \enspace\)\(E\) und \(F\) sind identisch.
|
\(B \notin E\) oder \(A \notin B\) \(\Longrightarrow \enspace\)\(E\) und \(F\) sind (echt) parallel (ggf. Abstand berechnen).
|
\(\Longrightarrow \enspace\)\(E\) und \(F\) schneiden sich in einer Schnittgeraden \(s\) unter dem Schnittwinkel \(\alpha\) (ggf. Gleichung der Schnittgeraden ermitteln und/oder Schnittwinkel berechnen.) |
|
Es gilt: \(\enspace x_{1_A} = \,x_{1_B} = \,x_{1_C} = 10\,\).
Somit liegt die Grundfläche \(ABC\) im Abstand \(d = 10\) in der zur \(x_2x_3\)-Ebene parallelen Ebene mit der Gleichung \(x_1 - 10 = 0\,\).
Die Grundfläche \(ABC\) repräsentiert ein Ebene, die parrallel zur \(x_2x_3\)-Ebene ist.
Volumen des Prismas \(ABCRST\)
Gerades Prisma \(ABCRST\)
1. Lösungsansatz: Grundfläche mal Höhe
Volumen eines geraden Prismas (vgl. Merkhilfe)
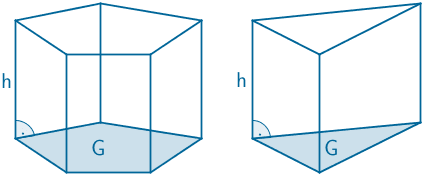
\[V_{\text{Prisma}} = G \cdot h\]
\[V_{ABCRST} = A_{ABC} \cdot h\]
Höhe \(h\) des Geraden Prismas berechnen:
\[h = \overline{AR} = \overline{BS} = \overline{CT}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}h &= \vert \overrightarrow{AR} \vert \\[0.8em] &= \vert \overrightarrow{R} - \overrightarrow{A} \vert \\[0.8em] &= \left| \begin{pmatrix} 2 \\ 2 \\ 0 \end{pmatrix} - \begin{pmatrix} 10 \\ 2 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} -8 \\ 0 \\ 0 \end{pmatrix}\right| \\[0.8em] &= \sqrt{(-8)^2 + 0^2 + 0^2} = 8 \end{align*}\]
Flächeninhalt der Grundfläche \(ABC\) berechnen:
Betrachtet wird eine Projektion der Grundfläche \(ABC\) in die \(x_2x_3\)-Ebene.
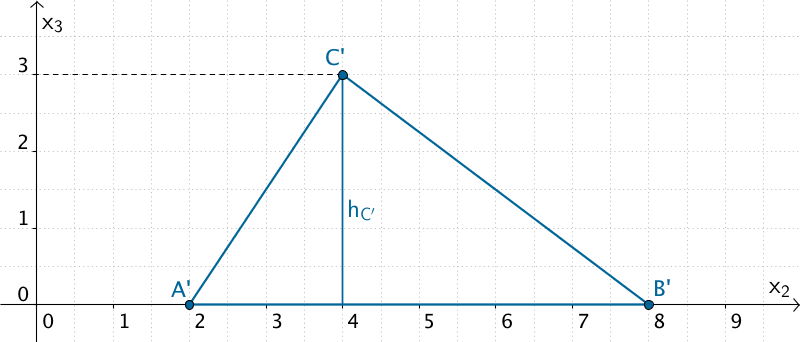
Projektion der Grundfläche \(ABC\) in die \(x_2x_3\)-Ebene
\(A'\,(0|2|0)\,\), \(B'\,(0|8|0)\,\), \(C'\,(0|4|3)\)
\[\begin{align*}A_{ABC} &= A_{A'B'C'} \\[0.8em] &= \frac{1}{2} \cdot (x_{2_{B'}} - x_{2_{A'}}) \cdot x_{3_{C'}} \\[0.8em] &= \frac{1}{2} \cdot (8 - 2) \cdot 3 \\[0.8em] &= 9 \end{align*}\]
Volumen des Prismas berechnen:
\[V_{ABCRST} = A_{ABC} \cdot h = 9 \cdot 8 = 72\]
2. Lösungsansatz: Anwenden des Vektorprodukts - Spatprodukt
Drei linear unabhängigen Vektoren, z.B. \(\,\overrightarrow{AB}\,\), \(\,\overrightarrow{AC}\,\) und \(\,\overrightarrow{AR}\,\), spannen einen Spat auf. Das Volumen des geraden Prismas \(\,ABCRST\,\) ist gleich dem halben Spatvolumen.
Anwendung des Vekorprodukts - Spatprodukt (vgl. Merkhilfe)
Volumen eines Spats
\[V_{\text{Spat}} = \left| \left( \overrightarrow{a} \times \overrightarrow{b} \right) \circ \overrightarrow{c} \; \right|\]
Volumen einer dreiseitigen Pyramide
\[V_{\text{Pyramide}} = \frac{1}{6} \left| \left( \overrightarrow{a} \times \overrightarrow{b} \right) \circ \overrightarrow{c} \; \right|\]
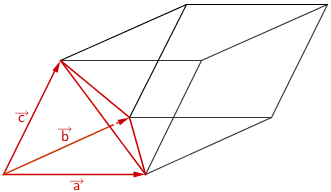
\[V_{ABCRST} = \frac{1}{2} \cdot \left| \left( \overrightarrow{AB} \times \overrightarrow{AC} \right) \circ \overrightarrow{AR} \; \right|\]
Linear unabhängige Vektoren bestimmen:
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 10 \\ 8 \\ 0 \end{pmatrix} - \begin{pmatrix} 10 \\ 2 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix}\]
\[\overrightarrow{AC} = \overrightarrow{C} - \overrightarrow{A} = \begin{pmatrix} 10 \\ 4 \\ 3 \end{pmatrix} - \begin{pmatrix} 10 \\ 2 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \\ 3 \end{pmatrix}\]
\[\overrightarrow{AR} = \overrightarrow{R} - \overrightarrow{A} = \begin{pmatrix} 2 \\ 2 \\ 0 \end{pmatrix} - \begin{pmatrix} 10 \\ 2 \\ 0 \end{pmatrix} = \begin{pmatrix} -8 \\ 0 \\ 0 \end{pmatrix}\]
Volumen des Prismas berechnen:
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin {align*} V_{ABCRST} &= \frac{1}{2} \cdot \left| \left( \overrightarrow{AB} \times \overrightarrow{AC} \right) \circ \overrightarrow{AR}\;\right| \\[0.8em] &= \frac{1}{2} \cdot \left| \left[ \begin {pmatrix} 0 \\ 6 \\ 0 \end {pmatrix} \times \begin {pmatrix} 0 \\ 2 \\ 3 \end {pmatrix} \right] \circ \begin {pmatrix} -8 \\ 0 \\ 0 \end {pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \left| \begin {pmatrix} 6 & \cdot & 3 & - & 0 & \cdot & 2 \\ 0 & \cdot & 0 & - & 0 & \cdot & 3 \\ 0 & \cdot & 2 & - & 6 & \cdot & 0 \end {pmatrix} \circ \begin {pmatrix} -8 \\ 0 \\ 0 \end {pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \left| \begin {pmatrix} 18 \\ 0 \\ 0 \end {pmatrix} \circ \begin {pmatrix} -8 \\ 0 \\ 0 \end {pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \left| 18 \cdot (-8) + 0 \cdot 0 + 0 \cdot 0 \right| \\[0.8em] &= 72 \end {align*}\]