Auf der Oberfläche der Marmorkugel treten an vier Stellen Wasserfontänen aus. Eine dieser Austrittsstellen wird im Modell durch den Punkt \(L_{0}(1|1|6)\) beschrieben. Die zugehörige Fontäne wird modellhaft durch Punkte \(L_{t}\left(t + 1|t + 1|6{,}2 - 5 \cdot (t - 0{,}2)^{2}\right)\) mit geeigneten Werten \(t \in \mathbb R_{0}^{+}\) beschrieben.
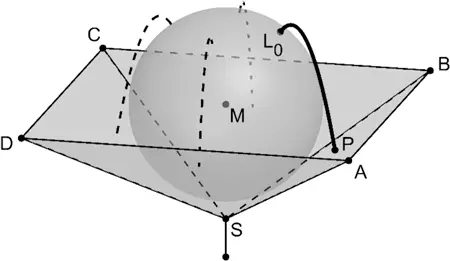
Der Punkt \(P\) liegt innerhalb des Dreiecks \(ABS\) und beschreibt im Modell die Stelle, an der die Fontäne auf die Bronzeschale trifft (vgl. Abbildung). Bestimmen Sie die Koordinaten von \(P\).
(4 BE)
Lösung zu Teilaufgabe f
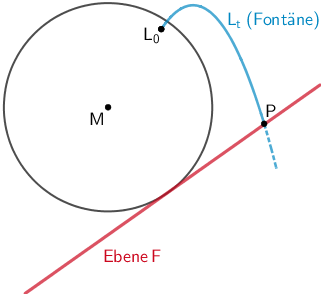
Planskizze (optional): Die Fontäne trifft im Punkt \(P\) auf das Dreieck \(ABS\) auf. Dieses liegt in der Ebene \(F\) (vgl. Teilaufgabe b). Somit ist der Punkt \(\boldsymbol{P}\) der Schnittpunkt der Kurve \(\textcolor{#0087c1}{L_{t}}\) (Fontäne) und der Ebene \(\textcolor{#cc071e}{F}\).
Für die Bestimmung der Koordinaten des Punktes \(P\) werden die Koordinaten von \(\textcolor{#0087c1}{L_{t}}\) in die Gleichung der Ebene \(\textcolor{#cc071e}{F}\) eingesetzt und diese nach dem Parameter \(t\) aufgelöst (analoge Vorgehensweise zu Schnittpunkt Gerade - Ebene).
\[\textcolor{#0087c1}{L_{t}}\left(\textcolor{#0087c1}{t + 1}|\textcolor{#0087c1}{t + 1}|\textcolor{#0087c1}{6{,}2 - 5 \cdot (t - 0{,}2)^{2}}\right)\]
\(\textcolor{#cc071e}{F}\colon x_{1} + x_{2} - 2x_{3} + 2 = 0\) (vgl. Teilaufgabe b)
\[\begin{align*}\textcolor{#0087c1}{L_{t}} \cap \textcolor{#cc071e}{F}\colon \textcolor{#0087c1}{t + 1} + \textcolor{#0087c1}{t + 1} - 2 \cdot \left[ \textcolor{#0087c1}{6{,}2 - 5 \cdot (t - 0{,}2)^{2}} \right] + 2 &= 0 \\[0.8em] 2t + 2 - 12{,}4 + 10 \cdot \textcolor{#e9b509}{(t - 0{,}2)^{2}} + 2 &= 0 &&| \; \textcolor{#e9b509}{\text{2. B. F.:}\; (a - b)^{2} = a^{2} - 2ab + b^{2}} \\[0.8em] 2t - 8{,}4 + 10 \cdot (\textcolor{#e9b509}{t^{2} - 0{,}4t + 0{,}04}) &= 0 \\[0.8em] 2t - 8{,}4 + 10t - 4t + 0{,}4 &= 0 \\[0.8em] 10t^{2} - 2t - 8 &= 0 &&| \; t \in \mathbb R_{0}^{+} \end{align*}\]
Lösungsformel für quadratische Gleichungen (Mitternachtsformel) verwenden:
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*} t_{1,2} &= \frac{2 \pm \sqrt{(-2)^{2} - 4 \cdot 10 \cdot (-8)}}{2 \cdot 10} &&|\; t \in \mathbb R_{0}^{+} \\[0.8em] &= \frac{2 \pm \sqrt{324}}{20} = \frac{2 \pm 18}{20} \\[0.8em] \Rightarrow \enspace \bigg( t_{1} &= \frac{2 - 18}{20} = -\frac{4}{5} \textcolor{#cc071e}{\not \in} \mathbb R_{0}^{+} \bigg) \\[0.8em] t_{2} &= \frac{2 + 18}{20} = 1\end{align*}\]
\(\textcolor{#e9b509}{t = 1}\) in \(\textcolor{#0087c1}{L_{t}}\) eingesetzt, ergibt die Koordinaten von \(P\).
\[P\left(\textcolor{#e9b509}{1} + 1|\textcolor{#e9b509}{1} + 1|6{,}2 - 5 \cdot (\textcolor{#e9b509}{1} - 0{,}2)^{2}\right) = P(2|2|3)\]


