Der Graph einer Stammfunktion von \(g\) verläuft durch \(P\). Skizzieren Sie diesen Graphen in Abbildung 2.
(3 BE)
Lösung zu Teilaufgabe 4b
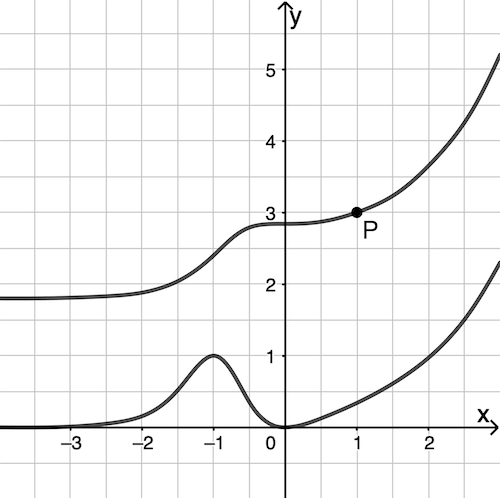Abb. 2
Graph einer Stammfunktion von \(g\) durch Punkt \(P\)
Ausführliche Erklärung (nicht verlangt)
Für eine Stammfunktion \(G\) der Funktion \(g\) gilt: \(G'(x) = g(x)\).
Stammfunktion
Eine differenzierbare Funktion \(F(x)\) heißt eine Stammfunktion von \(f(x)\), wenn
\(F'(x) = f(x)\) mit \(D_{F} = D_{f}\)
gilt.
Da der Graph von \(g\) bis auf den Tiefpunkt \((0|0)\) oberhalb der \(x\)-Achse verläuft, ist der Graph einer Stammfunktion \(\boldsymbol{G}\) streng monoton steigend.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Die Skizze sollte berücksichtigen, dass
- \(G_g\) sich für \(x \to -\infty\) asymptotisch der \(x\)-Achse annähert,
- \(G_g\) den Hochpunkt \((-1|1)\) und den Tiefpunkt \((0|0)\) besitzt,
- der Graph einer Stammfunktion \(G\) im Punkt \(P\) eine näherungsweise bestimmbare Steigung hat und
- \(G_g\) für \(x \to +\infty\) nach \(+\infty\) verläuft.
Verlauf des Graphen der Stammfunktion für \(x \to -\infty\)
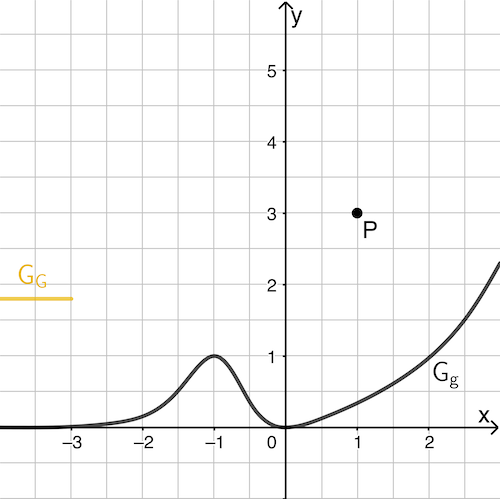Abb. 2
Für \(x \to -\infty\) nähert sich der Graph von \(g\) asymptotisch der \(x\)-Achse an. Somit gilt \(\lim \limits_{x\,\to\,-\infty} g(x) = \textcolor{#e9b509}{\lim \limits_{x\,\to\,-\infty} G'(x) = 0}\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Der Graph einer Stammfunktion beginnt daher horizontal. Da \(G_G\) streng monoton steigend ist und durch \(P\) verlaufen soll, wird die Skizze links und unterhalb von \(P\) begonnen.
Verlauf des Graphen der Stammfunktion an den Extremstellen von \(G_g\)
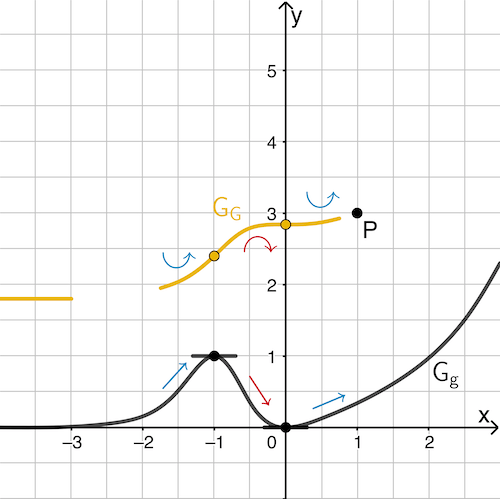Abb. 2
In den Extrempunkten bei \(x = -1\) und \(x = 0\) hat der Graph von \(g\) jeweils eine waagrechte Tangente und wechselt das Monotonieverhalten.
Somit gilt \(g'(-1) = \textcolor{#e9b509}{G''(-1) = 0}\) bzw. \(g'(0) = \textcolor{#e9b509}{G''(0) = 0}\) und \(g'(x) = \textcolor{#e9b509}{G''(x)}\) wechselt das Vorzeichen von \(\textcolor{#0087c1}{+}\) nach \(\textcolor{#cc071e}{–}\) bzw. von \(\textcolor{#cc071e}{–}\) nach \(\textcolor{#0087c1}{+}\).
Folglich sind die Extremstellen von \(g\) die Wendestellen einer Stammfunktion von \(g\).
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
An der Stelle \(x = -1\) des Hochpunkts von \(g\) erreicht die Steigung des Graphen der Stammfunktion mit \(g(-1) = \textcolor{#e9b509}{G'(-1) = 1}\) ein lokales Maximum.
An der Stelle \(x = 0\) des Tiefpunkts von \(g\) hat der Graph der Stammfunktion mit \(g(0) = \textcolor{#e9b509}{G'(0) = 0}\) eine waagrechte Wendetangente und deshalb einen Terrassenpunkt.
Anwendung der Differetialrechnung:
Terrassenpunkt
Wenn \(f'(x_0) = f''(x_0) = 0\) ist und \(f''\) an der Stelle \(x_0\) das Vorzeichen wechselt, so hat \(G_f\) an der Stelle \(x_0\) einen Terrassenpunkt.
Verlauf des Graphen der Stammfunktion im Punkt \(P\)
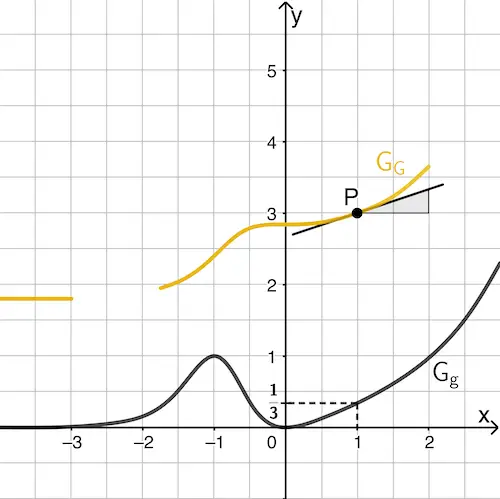Abb. 2
Näherungsweise gilt \(g(1) = \textcolor{#e9b509}{G'(1)} \approx \dfrac{1}{3}\). Also hat der Graph der Stammfunktion im Punkt P etwa die Steigung \(\textcolor{#e9b509}{\dfrac{1}{3}}\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Verlauf des Graphen der Stammfunktion für \(x \to +\infty\)
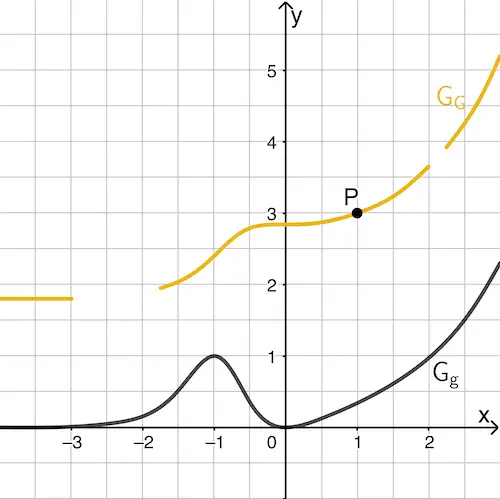Abb. 2
MIt \(\lim \limits_{x\,\to\,+\infty} g(x) = \textcolor{#e9b509}{\lim \limits_{x\,\to\,+\infty} G'(x)} = +\infty\) wächst die Steigung des Graphen der Stammfunktion für \(x \to +\infty\) nach \(+\infty\) und der Graph der Stammfunktion verläuft somit nach \(\textcolor{#e9b509}{+\infty}\).
Abschließend ergibt sich folgende Skizze:
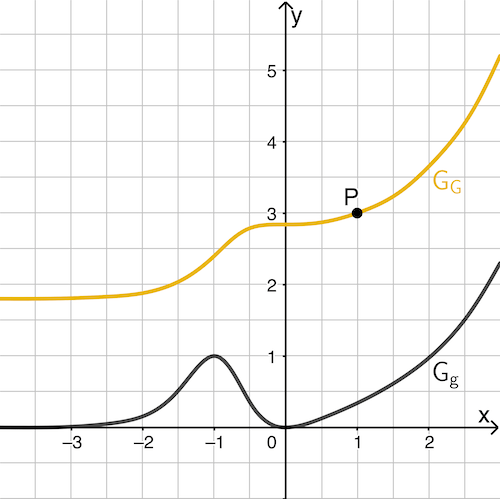Abb. 2
Graph einer Stammfunktion von \(g\) durch Punkt \(P\)
