Berechnen Sie die Größe des Winkels, unter dem die Seitenfläche
(3 BE)
Lösung zu Teilaufgabe c
Der Winkel, unter dem die Seitenfläche
Schnittwinkel zweier Ebenen
Schnittwinkel
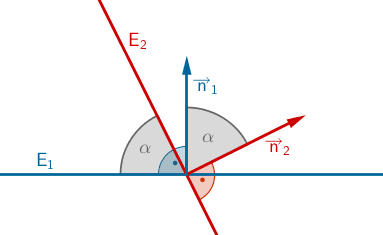
Schnittwinkel
Berechnen Sie die Größe des Winkels, unter dem die Seitenfläche
(3 BE)
Der Winkel, unter dem die Seitenfläche
Schnittwinkel

Schnittwinkel

mathelike.de ist ein privates Nachhilfe Projekt, das sich größtenteils durch Werbung finanziert.
Wir bitten um Beachtung des Copyright.