Die Funktion \(g\) ist nicht konstant und es gilt \(\displaystyle \int_{0}^{2} g(x) dx = 0\).
(2 BE)
Lösung zu Teilaufgabe 3b
Bestimmtes Integral geometrisch interpretieren, Entwicklung von Funktionen
Anmerkung:
Der Funktionsterm der gesuchten Funktion \(g\) ist lediglich anzugeben. Jede Erklärung kann entfallen.
Beispielsweise gilt \(\displaystyle \int_{0}^{2} g(x) dx = 0\) für:
\[g(x) = x - 1\]
oder
\[g(x) = (x - 1)^{3}\]
oder
\[g(x) = \sin(x - 1)\]
oder
\[g(x) = \sin(\pi \cdot x)\]
Erklärung:
Der Wert des Integrals \(\displaystyle \int_{0}^{2} g(x)\) entspricht der Flächenbilanz der Flächenstücke, welche der Graph der gesuchten Funktion \(g\) im Intervall \([0;2]\) mit der \(x\)-Achse einschließt. Flächenstücke unterhalb der \(x\)-Achse zählen negativ, Flächenstücke oberhalb der \(x\)-Achse zählen positiv.
Diese Flächenbilanz ist dann gleich Null \((\displaystyle \int_{0}^{2} g(x) dx = 0)\), wenn die Flächenstücke in den Intervallen \([0;1]\) und \([1;2]\) flächeninhaltsgleich sind, aber einmal unterhalb der \(x\)-Achse und einmal oberhalb der \(x\)-Achse liegen.
Der Graph einer Funktion \(g\), welcher die \(x\)-Achse an der Stelle \(x = 1\) schneidet (Nullstelle), und zu dieser punktsymmetrisch verläuft, erfüllt die angegebene Eigenschaft \(\displaystyle \int_{0}^{2} g(x) dx = 0\).
Denkt man sich also den Graphen einer zum Koordinatenursprung punktsymmetrischen Funktion, verschiebt diesen um eine Einheit in Richtung der positiven \(x\)-Achse und formuliert den zugehörigen Funktionsterm \(g\), so gilt \(\displaystyle \int_{0}^{2} g(x) dx = 0\).
1. Lösungsansatz: Potenzfunktion \(x \mapsto x^{n}\) ungerader Ordung
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
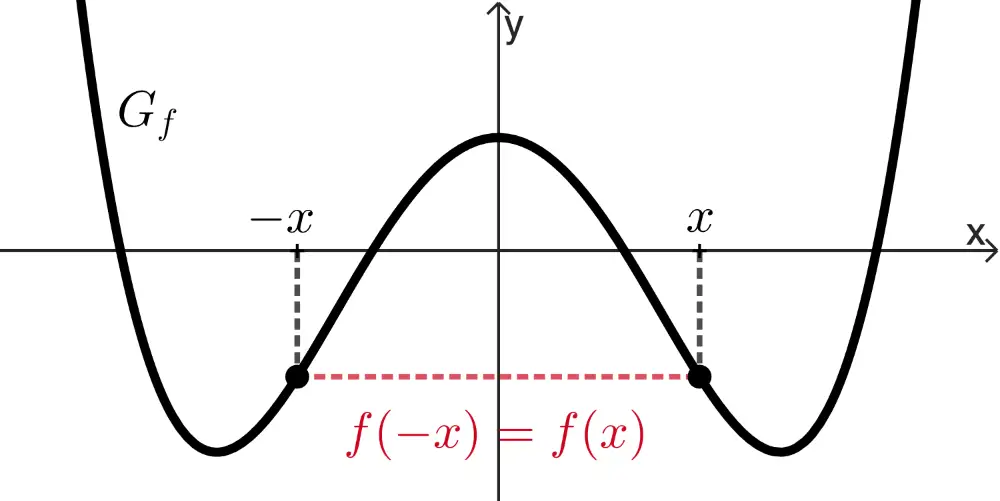
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
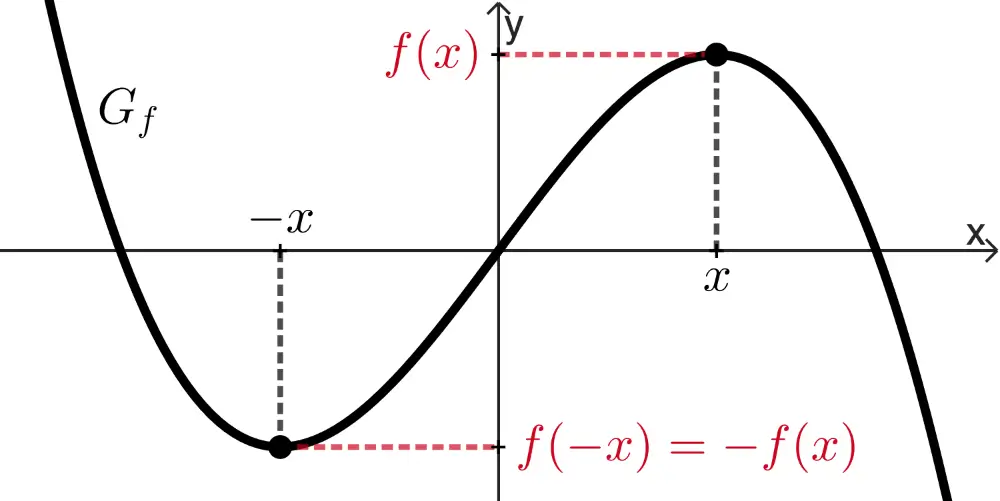
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
Für \(n = \{1;3;5 ...\}\) ist der Graph einer Potenzfunktion \(x \mapsto x^{n}\) punktsymmetrisch zum Koordinatenursprung. Verschiebt man beispielsweise den Graphen der Funktion \(x \mapsto x\) oder \(x \mapsto x^{3}\) um eine Einheit in Richtung der positiven \(x\)-Achse, ist der jeweils zugehörige Funktionsterm ein möglicher Funktionsterm \(g(x)\).
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\(g(x) = x-1\)
oder
\(g(x) = (x - 1)^3\)
Probe:
\[\begin{align*} \int_{0}^{2} (x - 1) dx &= \left[ \frac{1}{2}x - x \right]_{0}^{2} \\[0.8em] &= \frac{1}{2} \cdot 2^{2} - 2 - 0 \\[0.8em] &= 2 - 2 \\[0.8em] &= 0 \end{align*}\]
![Graph der Funktion x ↦ x, Flächenbilanz für x ∈ [0;2] Graph der Funktion x ↦ x, Flächenbilanz für x ∈ [0;2]](/images/stories/B2017_PT_A_A_1/B2017_PT_A_A_1_3b_1.png)
\(\displaystyle \int_{0}^{2} (x - 1) dx = 0\), Veranschaulichung als Flächenbilanz
\[\begin{align*} \int_{0}^{2} (x - 1)^{3} dx &= \int_{0}^{2} (x^{3} - 3x^{2} + 3x - 1) dx \\[0.8em] &= \left[ \frac{1}{4}x^{4} - x^{3} +\frac{3}{2}x^{2} - x \right]_{0}^{2} \\[0.8em] &= \frac{1}{4} \cdot 2^{4} - 2^{3} + \frac{3}{2} \cdot 2^{2} - 2 - 0 \\[0.8em] &= 4 - 8 + 6 - 2 \\[0.8em] &= 0 \end{align*}\]
![Graph der Funktion x ↦ x³, Flächenbilanz für x ∈ [0;2] Graph der Funktion x ↦ x³, Flächenbilanz für x ∈ [0;2]](/images/stories/B2017_PT_A_A_1/B2017_PT_A_A_1_3b_2.png)
\(\displaystyle \int_{0}^{2} (x - 1)^{3} dx = 0\), Veranschaulichung als Flächenbilanz
2. Lösungsansatz: Sinusfunktion \(x \mapsto \sin{x}\)
Der Graph der Sinusfunktion \(x \mapsto \sin{x}\) besitzt für \(k \cdot \pi\) mit \(k \in \mathbb Z\) Nullstellen und ist zu diesen jeweils punktsymmetrisch. \(x = 0\) ist eine dieser Nullstellen. Die Sinusfunktion \(x \mapsto \sin{x}\) ist also zum Koordinatenursprung punktsymmetrisch.
Verschiebt oder steckt/staucht man den Graphen der Sinusfunktion \(x \mapsto \sin{x}\) so, dass \(x = 1\) eine Nullstelle des Graphen der entstehenden Sinusfunktion ist, und formuliert den zugehörigen Funktionsterm \(g\), so gilt \(\displaystyle \int_{0}^{2} g(x) dx = 0\).
Verschiebung des Graphen der Sinusfunktion \(x \mapsto \sin{x}\):
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
Der Graph der Sinusfunktion \(x \mapsto \sin{x}\) wird um eine Einheit in Richtung der positiven \(x\)-Achse verschoben und der zugehörige Funktionsterm \(g\) formuliert. Dann ist \(x = 1\) Nullstelle von \(g\) und es gilt \(\displaystyle \int_{0}^{2} g(x) dx = 0\).
\[g(x) = \sin{(x - 1)}\]
Probe:
\[\begin{align*} \int_{0}^{2} \sin{(x - 1)} dx &= \left[ -\cos{(x - 1)} \right]_{0}^{2} \\[0.8em] &= -\cos{1} - (-\cos {(-1)}) & &| \; \cos{(-1)} = \cos{1} \\[0.8em] &= -\cos{1} + \cos{1} \\[0.8em] &= 0 \end{align*}\]
![Graph der Sinusfunktion x ↦ sin(x - 1), Flächenbilanz für x ∈ [0;2] Graph der Sinusfunktion x ↦ sin(x - 1), Flächenbilanz für x ∈ [0;2]](/images/stories/B2017_PT_A_A_1/B2017_PT_A_A_1_3b_3.png)
\(\displaystyle \int_{0}^{2} \sin{(x - 1)} dx = 0\), Veranschaulichung als Flächenbilanz
Streckung/Stauchung des Graphen der Sinusfunktion:
Allgemeine Sinusfunktion
\[f(x) = a \cdot \sin(bx + c) + d = a \cdot \sin \left[b \left(x + \frac{c}{b} \right) \right] + d\]
\[a,b,c,d \in \mathbb R\;; \quad a,b \neq 0\;; \quad x \in \mathbb R\]
Streckung um \(a\) in \(y\)-Richtung
Streckung um \(\displaystyle \frac{1}{b}\) in \(x\)-Richtung, Periode: \(\displaystyle p = \frac{2\pi}{\vert b \vert}\)
Verschiebung um \(\displaystyle -\frac{c}{b}\) in \(x\)-Richtung
Verschiebung um \(d\) in \(y\)-Richtung
Ansatz: \(x \mapsto \sin{(b \cdot x)}; \; b > 0\)
Der Graph der Sinusfunktion \(x \mapsto \sin{x}\) wird mit dem Faktor \(\frac{1}{b}\) in \(x\)-Richtung gestreckt bzw. mit dem Faktor \(b\) in \(x\)-Richtung gestaucht. \(x = 1\) soll Nullstelle der entstehenden Sinusfunktion \(x \mapsto \sin{(b \cdot x)}\) sein.
\[\begin{align*} \sin{(b \cdot x)} &= 0 & &| \; x = 1 \\[0.8em] \sin{(b \cdot 1)} &= 0 & &| \; \sin{x} = 0 \; \text{für} \; x = k \cdot \pi; \; k \in \mathbb Z \\[1.6em] \Longrightarrow \quad b &= k \cdot \pi & &(b > 0) \end{align*}\]
Beispielsweise wählt man \(b = \pi\) für \(k = 1\). Dies entspricht einer Streckung des Graphen der Sinusfunktion \(x \mapsto \sin{x}\) mit dem Faktor \(\frac{1}{\pi}\) in \(x\)-Richtung bzw. einer Stauchung mit dem Faktor \(\pi\) in \(x\)-Richtung.
\[g(x) = \sin{(\pi \cdot x)}\]
Probe:
\[\begin{align*} \int_{0}^{2} \sin{(\pi \cdot x)} dx &= \left[ -\frac{1}{\pi} \cdot \cos{(\pi \cdot x)} \right]_{0}^{2} \\[0.8em] &= -\frac{1}{\pi} \cdot \cos{2\pi} - \left( -\frac{1}{\pi} \cdot \cos{0} \right) \\[0.8em] &= -\frac{1}{\pi} \cdot 1 + \frac{1}{\pi} \cdot 1 \\[0.8em] &= 0 \end{align*}\]
![Graph der Sinusfunktion x ↦ sin(π・x), Flächenbilanz für x ∈ [0;2] Graph der Sinusfunktion x ↦ sin(π・x), Flächenbilanz für x ∈ [0;2]](/images/stories/B2017_PT_A_A_1/B2017_PT_A_A_1_3b_4.png)
\(\displaystyle \int_{0}^{2} \sin{(\pi \cdot x)} dx = 0\), Veranschaulichung als Flächenbilanz


