Der Hersteller des Sonnensegels empfiehlt, die verwendeten Metallstangen bei einer Sonnensegelfläche von mehr als 20 m² durch zusätzliche Sicherungsseile zu stabilisieren. Beurteilen Sie, ob eine solche Sicherung aufgrund dieser Empfehlung in der vorliegenden Situation nötig ist
(3 BE)
Lösung zu Teilaufgabe b
Es ist der Flächeninhalt \(A\) des Sonnensegels (Dreieck \(S_{1}S_{2}S_{3}\)) zu berechnen und mit der Herstellerermpfehlung zu vergleichen.
Der Flächeninhalt \(A\) lässt sich mithilfe des Vektorprodukts berechnen.
Anwendung des Vekorprodukts
Der Betrag des Vektorprodukts \(\overrightarrow{a} \times \overrightarrow{b}\) entspricht der Maßzahl des Flächeninhalts eines von zwei Vektoren \(\overrightarrow{a} \neq \overrightarrow{0}\) und \(\overrightarrow{b} \neq \overrightarrow{0}\) aufgespannten Parallelogramms.
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \textcolor{#cc071e}{\vert \overrightarrow{b} \vert \cdot \sin{\varphi}}\]
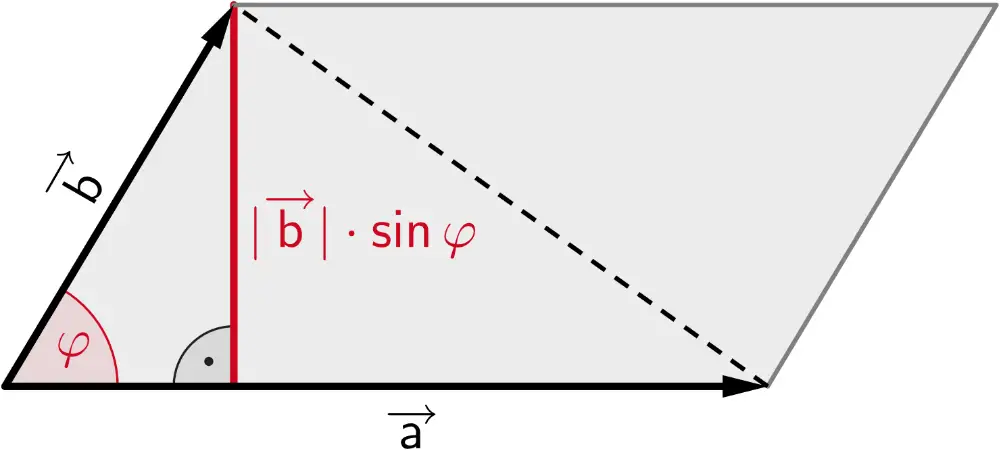
Flächeninhalt eines Parallelogramms
\[A = \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
Flächeninhalt eines Dreiecks
\[A = \frac{1}{2} \cdot \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
Aus Teilaufgabe a ist das Vektorprodukt \(\overrightarrow{S_{2}S_{1}} \times \overrightarrow{S_{2}S_{3}} = \begin{pmatrix} -3 \\ -3 \\ -36 \end{pmatrix}\) bereits bekannt.
\[\begin{align*} A&= \frac{1}{2} \cdot \vert \overrightarrow{S_{s}S_{1}} \times \overrightarrow{S_{2}S_{3}} \vert \\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} -3 \\ -3 \\ -36 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \sqrt{(-3)^{2} + (-3)^{2} + (-36)^{|2}} \\[0.8em] &\approx 18{,}1 \end{align*}\]
Beurteilung:
Mit ca. 18,1 m² ist der Flächeninhalt des Sonnensegels kleiner als die vom Hersteller genannte kritische Fläche von 20 m². Eine zusätzliche Stabilisierung durch Sicherungsseile ist daher nicht notwendig.


