In einer Urne befinden sich 20 Kugeln, darunter 12 weiße Kugeln und 8 rote Kugeln. Aus der Urne werden nacheinander zwei Kugeln ohne Zurücklegen entnommen.
Die Zufallsgröße \(X\) beschreibt die Anzahl der entnommenen roten Kugeln.
a) Erstellen Sie ein vollständig ausgefülltes Baumdiagramm.
b) Bestimmen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) und geben Sie diese tabellarisch an.
c) Ermitteln Sie den Erwartungswert und die Standardabweichung der Zufallsgröße \(X\).
d) Berechnen Sie die Wahrscheinlichkeit dafür, dass die Zufallsgröße \(X\) einen Wert annimmt, der höchstens um die einfache Standardabweichung vom Erwartungswert abweicht.
a) Vollständig ausgefülltes Baumdiagramm
Betrachtet werden folgende Ereignisse:
\(W\): „Die entnommene Kugel ist Weiß."
\(R\): „Die entnommene Kugel ist Rot."
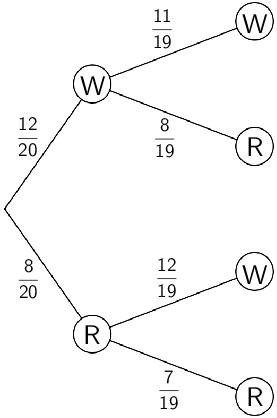
Im ersten Durchgang befinden sich 20 Kugeln in der Urne. Da die entnommene Kugel nicht zurückgelegt wird, befinden sich im zweiten Durchgang nur noch 19 Kugeln in der Urne.
Im ersten Durchgang gibt es 20 gleichwahrscheinliche Möglichkeiten \((\vert \Omega \vert = 20)\) und im zweiten Durchgang gibt es 19 gleichwahrscheinliche Möglichkeiten \((\vert \Omega \vert = 19)\), eine beliebige Kugel zu ziehen. Die Entnahme einer Kugel kann somit als Laplace-Experiment betrachtet werden (vgl. Abiturskript - 3.1.3 Laplace-Experiment, Laplace-Wahrscheinlichkeit) und es gilt jeweils:
Laplace-Wahrscheinlichkeit eines Ereignisses \(A\)
\[P(A) = \frac{\vert A \vert}{\vert \Omega \vert} = \frac{\text{Anzahl der für} \; A \; \text{günstigen Ergebnisse}}{\text{Anzahl der möglichen Ergebnisse}}\]
Voraussetzung: Alle Ergebnisse (alle Versuchsausgänge) des betrachteten Zufallsexperiments sind gleichwahrscheinlich (Laplace-Experiment).
\[P(W) = \frac{\vert W \vert}{\vert \Omega \vert} \qquad P(R) = \frac{\vert R \vert}{\vert \Omega \vert}\]
b) Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) mit Tabelle
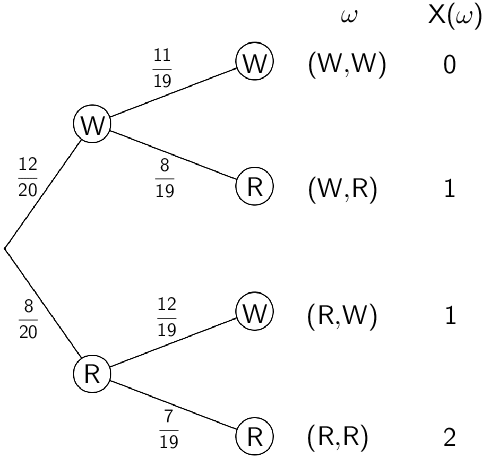
Die Zufallsgröße \(X\) beschreibt die Anzahl der entnommenen roten Kugel und kann die Werte \(x_{1} = 0\), \(x_{2} = 1\) und \(x_{3} = 2\) annehmen.
Die Wahrscheinlichkeiten dafür, dass die Zufallsgröße \(X\) einen Wert \(x_{i}\) annimmt, lassen sich mithilfe der Pfadregeln bestimmen.
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Nach der ersten Pfadregel gilt:
\[P(X = 0) = P(W,W) = \frac{12}{20} \cdot \frac{11}{19} = \frac{132}{380}\]
\[P(X = 2) = P(R,R) = \frac{8}{20} \cdot \frac{7}{19} = \frac{56}{380}\]
Nach der ersten und zweiten Pfadregel gilt:
\[\begin{align*}P(X = 1) &= P(W,R) + P(R,W) \\[0.8em] &= \underbrace{\underbrace{\frac{12}{20} \cdot \frac{8}{19}}_{\large{\text{1. Pfadregel}}} + \underbrace{\frac{8}{20} \cdot \frac{12}{19}}_{\large{\text{1. Pfadregel}}}}_{\large{\text{2. Pfadregel}}} \\[0.8em] &= \frac{96}{380} + \frac{96}{380} \\[0.8em] &= \frac{192}{380} \end{align*}\]
Tabelle der Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\):
| \(X = x_{i}\) | \(0\) | \(1\) | \(2\) |
| \(P(X = x_{i})\) | \(\dfrac{132}{380}\) | \(\dfrac{192}{380}\) | \(\dfrac{56}{380}\) |
c) Erwartungswert und Standardabweichung der Zufallsgröße \(X\)
(vgl. Abiturskript - 3.3.2 Erwartungswert, Varianz und Standardabweichung einer Zufallsgröße)
Erwartungswert \(E(X)\) der Zufallsgröße \(X\):
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) der Zufallsgröße \(\boldsymbol{X}\) (vgl. Merkhilfe)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot p_{i} \\[0.8em] &= x_{1} \cdot p_{1} + x_{2} \cdot p_{2} \,+\, ... \,+\, x_{n} \cdot p_{n} \end{align*}\]
Der Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(X\) gibt den Mittelwert der Zufallsgröße an, der bei oftmaliger Wiederholung eines Zufallsexperiments zu erwarten ist.
\[\begin{align*} \mu = E(X) &= x_{1} \cdot P(X = x_{1}) + x_{2} \cdot P(X = x_{2}) + x_{3} \cdot P(X = x_{3}) \\[0.8em] &= 0 \cdot \frac{132}{380} + 1 \cdot \frac{192}{380} + 2 \cdot \frac{56}{380} \\[0.8em] &= \frac{304}{380} \\[0.8em] &= 0{,}8 \end{align*}\]
Standardabweichung \(\sigma\) der Zufallsgröße \(X\):
Mit \(\sigma = \sqrt{Var(X)}\) wird zunächst die Varianz \(Var(X)\) der Zufallsgröße \(X\) berechnet.
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Varianz \(\boldsymbol{Var(X)}\) der Zufallsgröße \(\boldsymbol{X}\)
\[\begin{align*}Var(X) \enspace = \quad &\sum \limits_{i\;=\;1}^{n} (x_{i} - \mu)^{2} \cdot P(X = x_{i}) \\[0.8em] \enspace = \quad &(x_{1} - \mu)^{2} \cdot P(X = x_{1}) + (x_{2} - \mu)^{2} \cdot P(X = x_{2}) + \dots \\[0.8em] + \; &(x_n - \mu)^2 \cdot P(X = x_n)\end{align*}\]
Die Varianz \(\boldsymbol{Var(X)}\) einer Zufallsgröße \(X\) ist eine Maßzahl für die Streuung der Werte \(x_{i}\) der Zufallsgröße um den Erwartungswert \(\mu\).
\[\begin{align*} Var(X) &= (x_{1} - \mu)^{2} \cdot P(X = x_{1}) + (x_{2} - \mu)^{2} \cdot P(X = x_{2}) + (x_{3} - \mu)^{2} \cdot P(X = x_{3}) \\[0.8em] &= (0 - 0{,}8)^{2} \cdot \frac{132}{380} + (1 - 0{,}8)^{2} \cdot \frac{192}{380} + (2 - 0{,}8)^{2} \cdot \frac{56}{380} \\[0.8em] &= \frac{526}{2375} + \frac{48}{2375} + \frac{504}{2375} \\[0.8em] &= \frac{1078}{2375} \\[0.8em] &\approx 0{,}45 \end{align*}\]
\[\sigma = \sqrt{Var(X)} = \sqrt{\frac{1078}{2375}} \approx 0{,}67\]
d) Wahrscheinlichkeit dafür, dass die Zufallsgröße \(X\) einen Wert annimmt, der höchstens um die einfache Standardabweichung vom Erwartungswert abweicht
Der kleinste Wert, den die Zufallsgröße \(X\) annehmen kann ist \(\mu - \sigma\) und der größte Wert ist \(\mu + \sigma\).
Gesucht ist also die Wahrscheinlichkeit \(P(\mu - \sigma \leq X \leq \mu + \sigma)\).
Grenzen \(\mu - \sigma\) und \(\mu + \sigma\) berechnen:
\(\mu = 0{,}8\), \(\sigma = 0{,}67\) (vgl. Teilaufgabe a)
\[\mu - \sigma = 0{,}8 - 0{,}67 = 0{,}13\]
\[\mu + \sigma = 0{,}8 + 0{,}67 = 1{,}47\]
Damit ergibt sich:
\(P(\mu - \sigma \leq X \leq \mu + \sigma) = P(0{,}13 \leq X \leq 1{,}47)\) mit \(x_{i} = \{ 0;1;2\}\)
Da die Zufallsgröße \(X\) nur die Werte \(x_{1} = 0\), \(x_{2} = 1\) und \(x_{3} = 2\) annehmen kann, folgt:
\[\begin{align*} P(\mu - \sigma \leq X \leq \mu + \sigma) &= P(0{,}13 \leq X \leq 1{,}47) \\[0.8em] &= P(X = 1) \\[0.8em] &= \frac{192}{380} \\[0.8em] &= \frac{48}{95} \\[0.8em] &\approx 0{,}51 \end{align*}\]

