Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{1}{32}x^{4} - \dfrac{1}{4}x^{2} + 1\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Untersuchen Sie das Symmetrieverhalten von \(f\).
b) Untersuchen Sie das Verhalten von \(G_{f}\) für \(x \to -\infty\) und \(x \to +\infty\).
c) Bestimmen Sie die Gleichung der Tangente \(T\) im Punkt \(P(1|f(1))\).
d) Berechnen Sie den Schnittpunkt \(S_{y}\) des Graphen der Funktion \(f\) mit der \(y\)-Achse.
e) Bestimmen Sie rechnerisch Lage und Art aller Extrempunkte von \(G_{f}\).
f) Zeichnen Sie \(G_{f}\) sowie die Tangente \(T\) unter Berücksichtigung der bisherigen Ergebnisse in ein geeignetes Koordinatensystem.
Die ganzrationale Funktion \(f\) ist in \(\mathbb R\) definiert.
\[f(x) = \frac{1}{32}x^{4} - \frac{1}{4}x^{2} + 1; \, D_{f} = \mathbb R\]
a) Symmetrieverhalten von \(f\)
Man bestimmt den Funktionsterm \(f(-x)\). Gilt \(f(-x) = f(x)\), ist \(G_{f}\) achsensymmetrisch zur \(y\)-Achse. Gilt \(f(-x) = -f(x)\), ist \(G_{f}\) punktsymmetrisch zum Koordinatenursprung \(O(0|0)\). Trifft keiner der beiden Fälle zu, weist \(G_{f}\) keines der beiden Symmetrieverhalten auf.
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
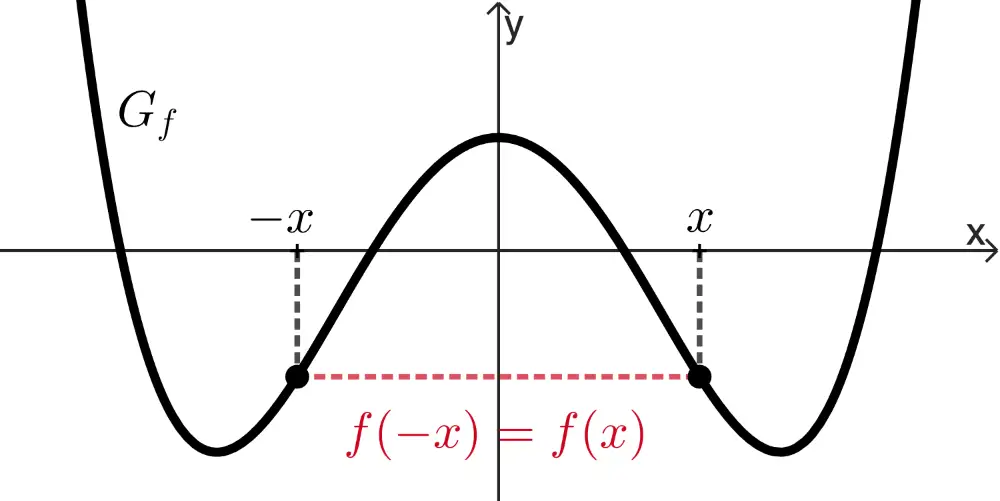
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
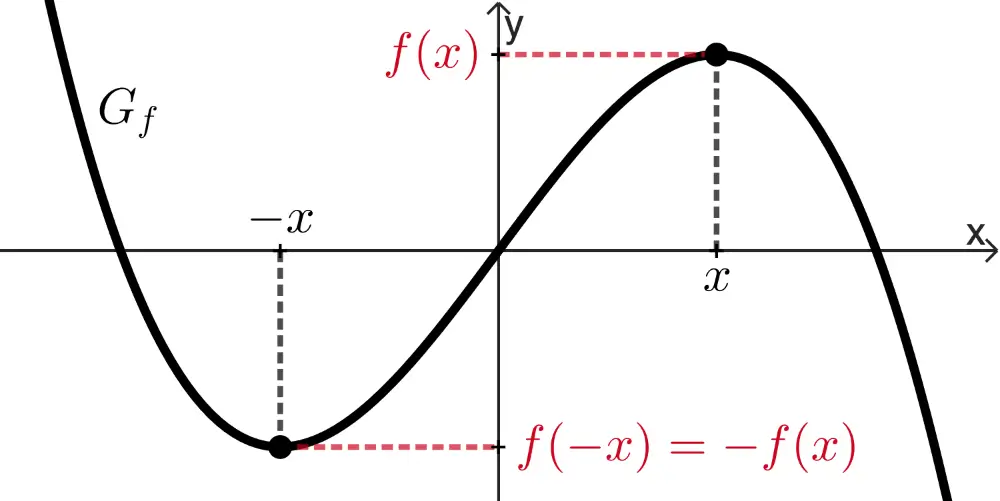
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[\begin{align*}f(-x) &= \frac{1}{32}(-x)^{4} - \frac{1}{4}(-x)^{2} + 1 \\[0.8em] &=\frac{1}{32}x^{4} - \frac{1}{4}x^{2} + 1 \\[0.8em] &= f(x) \end{align*}\]
\(\Longrightarrow \quad G_{f}\) ist achsensymmetrisch zur \(y\)-Achse.
Alternative Begründung:
Da der Funktionsterm der ganzrationalen Funktion \(f\) ausschließlich gerade Potenzen enthält, verläuft \(G_{f}\) achsensymmetrisch zur \(y\)-Achse.
b) Verhalten von \(G_{f}\) für \(x \to -\infty\) und \(x \to +\infty\)
Bei einer ganzrationalen Funktion bestimmt die höchste vorkommende Potenz sowie deren Koeffizient (Faktor der Potenz) das Verhalten des Graphen der Funktion im Unendlichen.
\[f(x) = \frac{1}{32}x^{4} - \frac{1}{4}x^{2} + 1; \, D_{f} = \mathbb R\]
\(\Longrightarrow \quad\)Der Term \(\frac{1}{32}x^{4}\) bestimmt das Verhalten von \(G_{f}\) im Unendlichen.
Wegen der in Teilaufgabe a festgestellten Achsensymmetrie von \(G_{f}\) bzgl. der \(y\)-Achse, können die Grenzwertbetrachtungen für \(x \to -\infty\) und \(x \to +\infty\) zusammengefasst werden.
\[\lim \limits_{x\,\to\,\pm\infty} f(x) = \lim \limits_{x\,\to\,\pm\infty} \frac{1}{32}x^{4} = +\infty\]
c) Gleichung der Tangente \(T\) im Punkt \(P(1|f(1))\)
\[f(x) = \frac{1}{32}x^{4} - \frac{1}{4}x^{2} + 1; \, D_{f} = \mathbb R\]
\[P(1|f(1))\]
Der Ansatz für die Gleichung der Tangente \(T\) kann mithilfe der allgemeinen Geradengleichung oder mit der Tangentengleichung erfolgen.
1. Lösungsansatz: Allgemeine Geradengleichung
Allgemeine Geradengleichung
\[y = mx + t\]
Wobei \(m\) die Steigung und \(t\) der \(y\)-Achsenabschnitt der Geraden ist.
\[T \colon y = m_{T} \cdot x + t\]
Die erste Ableitung \(f'\) an der Stelle \(x = 1\) beschreibt die Steigung \(m_{T}\) der Tangente \(T\) an den Graphen der Funktion \(f\) im Punkt \(P(1|f(1))\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[m_{T} = f'(1)\]
Erste Ableitung \(f'\) bilden:
Die Erste Ableitung \(f'\) der ganzrationalen Funktion \(f\) lässt sich mit der Ableitung einer Potenzfunktion, der Summenregel und der Faktorregel formulieren.
\[f(x) = \frac{1}{32}x^{4} - \frac{1}{4}x^{2} + 1\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*} f'(x) &= \frac{1}{32} \cdot 4 \cdot x^{3} - \frac{1}{4} \cdot 2 \cdot x + 0 \\[0.8em] &= \frac{1}{8}x^{3} - \frac{1}{2}x \end{align*}\]
Tangentensteigung \(m_{T}\) berechnen:
\[\begin{align*}m_{T} &= f'(1) \\[0.8em] &= \frac{1}{8} \cdot 1^{3} - \frac{1}{2} \cdot 1 \\[0.8em] &= -\frac{3}{8} \end{align*}\]
Damit ergibt sich die Gleichung der Tangente \(T\) zu:
\[T \colon y = -\frac{3}{8}x + t\]
\(y\)-Achsenabschnitt \(t\) der Tangente \(T\) bestimmen:
Die Tangente \(T\) berührt den Graphen der Funktion \(f\) im Punkt \(P(1|f(1))\; (P \in T)\). Setzt man die Koordinaten des Punktes \(P\) in die Gleichung der Tangente \(T\) ein, lässt sich damit der \(y\)-Achsenabschnit \(t\) bestimmen. Vorab ist noch der Funktionswert \(f(1)\) zu berechnen.
\[f(x) = \frac{1}{32}x^{4} - \frac{1}{4}x^{2} + 1\]
\[\begin{align*}f(1) &= \frac{1}{32} \cdot 1^{4} - \frac{1}{4} \cdot 1^{2} + 1 \\[0.8em] &= \frac{1}{32} - \frac{1}{4} + 1 \\[0.8em] &= \frac{1}{32} - \frac{8}{32} + \frac{32}{32} \\[0.8em] &= \frac{25}{32} \\[0.8em] &\approx 0{,}78 \end{align*}\]
\[\Longrightarrow \quad P \Big(1| \textstyle \frac{25}{32}\Big)\]
\[\begin{align*} P \in T \colon \frac{25}{32} &= -\frac{3}{8} \cdot 1 + t \\[0.8em] \frac{25}{32} &= -\frac{3}{8} + t & &| + \frac{3}{8} \\[0.8em] \frac{25}{32} + \frac{3}{8} &= t \\[0.8em] \frac{25}{32} + \frac{12}{32} &= t \\[0.8em] \frac{37}{32} &= t \\[0.8em] 1{,}16 &\approx t \end{align*}\]
Gleichung der Tangente \(T\) angeben:
\[T \colon y = -\frac{3}{8}x + \frac{37}{32}\]
2. Lösungsansatz: Tangentengleichung
Gleichung einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\;(x_0|f(x_0)) \):
\[y = f'(x_{0}) \cdot (x - x_{0}) + f(x_{0})\]
\[P(1|f(1))\]
\[T \colon y = f'(1) \cdot (x - 1) + f(1)\]
Mit \(f'(1) = -\frac{3}{8}\) und \(f(1) = \frac{25}{32}\) (vgl. 1. Lösungsansatz) folgt:
\[\begin{align*}T \colon y &= f'(1) \cdot (x - 1) + f(1) \\[0.8em] &= -\frac{3}{8} \cdot (x - 1) + \frac{25}{32} \\[0.8em] &= -\frac{3}{8}x + \frac{3}{8} + \frac{25}{32} \\[0.8em] &= -\frac{3}{8}+ + \frac{12}{32} + \frac{25}{32} \\[0.8em] &= -\frac{3}{8}x + \frac{37}{32} \end{align*}\]
d) Schnittpunkt \(S_{y}\) von \(G_{f}\) mit der \(y\)-Achse
Der Schnittpunkt \(S_{y}\) von \(G_{f}\) mit der \(y\)-Achse hat die Koordinaten \(S_{y}(0|f(0))\). Es ist also der Funktionswert \(f(0)\) zu berechnen.
\[f(x) = \frac{1}{32}x^{4} - \frac{1}{4}x^{2} + 1\]
\[f(0) = \frac{1}{32} \cdot 0^{4} - \frac{1}{4} \cdot 0^{2} + 1 = 1\]
\[\Longrightarrow \quad S_{y}(0|1)\]
e) Lage und Art aller Extrempunkte von \(G_{f}\)
An den Extremstellen besitzt der Graph der Funktion \(f\) eine waagrechte Tangente, das heißt, die Tangentensteigung ist gleich Null. Die erste Ableitung \(f'\) der Funktion \(f\) beschreibt die Steigung einer Tangente an den Graphen der Funktion \(f\),
Folglich lautet die notwendige Bedingung für einen Extrempunkt von \(G_{f}\):
\[f'(x) = 0\]
Der Funktionsterm \(f'(x)\) ist bereits aus Teilaufgabe c bekannt.
\[f'(x) = \frac{1}{8}x^{3} - \frac{1}{2}x\]
Nullstellen von \(f'\) bestimmen:
\[\begin{align*} f'(x) &= 0 \\[0.8em] \frac{1}{8}x^{3} - \frac{1}{2}x &= 0 & &| \; x \; \text{ausklammern (Term in Produkt umformen)} \\[0.8em] x \cdot \left( \frac{1}{8}x^{2} - \frac{1}{2} \right) &= 0 \end{align*}\]
Ein Produkt ist dann gleich Null, wenn mindestens einer der Faktoren gleich Null ist.
\[\Longrightarrow \quad x_{1} = 0 \; \vee \; \frac{1}{8}x^{2} - \frac{1}{2} = 0\]
Die (rein)quadratische Gleichung \(\frac{1}{8}x^{2} - \frac{1}{2} = 0\) hat maximal zwei reelle Lösungen.
\[\begin{align*} \frac{1}{8}x^{2} - \frac{1}{2} &= 0 & &| + \frac{1}{2} \\[0.8em] \frac{1}{8}x^{2} &= \frac{1}{2} & &| \cdot 8 \\[0.8em] x^{2} &= 4 & &| \; \sqrt{\quad} \\[0.8em] x_{2,3} &= \pm 2 \end{align*}\]
An den Stellen \(x_{1} = 0\), \(x_{2} = -2\) und \(x_{3} = 2\) besitzt \(G_{f}\) jeweils eine waagrechte Tangente, welche auf einen Extrem- oder Terrassenpunkt hinweist.
Nachweis der Extrempunkte und deren Art:
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
Ein Extrempunkt liegt an den Stellen \(x_{1} = 0\), \(x_{2} = -2\) bzw. \(x_{3} = 2\) dann vor, wenn \(f'\) dort das Vorzeichen wechselt, das heißt, wenn \(G_{f}\) gemäß dem Monotoniekriterium das Monotonieverhalten ändert.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Um den Vorzeichenwechsel von \(f'\) besser beurteilen und dokumentieren zu können, ist es zweckmäßig, den Funktionsterm \(f'(x)\) in seiner vollständig faktorisierten Form zu beschreibt. Mithilfe der Nullstellen \(x_{1} = 0\), \(x_{2} = -2\) und \(x_{3} = 2\) von \(f'\) bzw. durch Anwenden der 3. Binomischen Formel ergibt sich:
\[\begin{align*}f'(x) &= x \cdot \left( \frac{1}{8}x^{2} -\frac{1}{2} \right) \\[0.8em] &= x \cdot \frac{1}{8} \cdot (\underbrace{x^{2} - 4}_{\large{a^{2}\,-\,b^{2}}}) & &| \; \text{3. Binomische Formel anwenden} \\[0.8em] &= \frac{1}{8}x\underbrace{(x - 2)(x + 2)}_{\large{(a\,-\,b)(a\,+\,b)}} \end{align*}\]
\[\left. \begin{align*} &f'(x) < 0 \; \text{für} \; x < -2 \\[0.8em] &f'(-2) = 0 \\[0.8em] &f'(x) > 0 \; \text{für} \; -2 < x < 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt}\; TiP(-2|f(-2))\]
\[\left. \begin{align*} &f'(x) > 0 \; \text{für} \; -2 < x < 0 \\[0.8em] &f'(0) = 0 \\[0.8em] &f'(x) < 0 \; \text{für} \; 0 < x < 2 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkt}\; HoP(0|f(0))\]
\[\left. \begin{align*} &f'(x) < 0 \; \text{für} \; 0 < x < 2 \\[0.8em] &f'(2) = 0 \\[0.8em] &f'(x) > 0 \; \text{für} \; x > 2 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt}\; TiP(2|f(2))\]
Alternative:
Aufgrund der in Teilaufgabe a festgestellten Achsensymmetrie von \(G_{f}\) bzgl. der \(y\)-Achse genügt der Nachweis eines der beiden Tiefpunkte. Das Symmetrieverhalten von \(G_{f}\) begründet jeweils die Existenz des zweiten Tiefpunkts.
Veranschaulichung mithilfe einer Monotonietabelle:
\[f'(x) = \frac{1}{8}x(x - 2)(x + 2)\]
| \(x\) | \(x < -2\) | \(-2\) | \(-2 < x < 0\) |
| \(\frac{1}{8}x\) | \(-\) | \(-\) | \(-\) |
| \((x - 2)\) | \(-\) | \(-\) | \(-\) |
| \((x + 2)\) | \(-\) | \(0\) | \(+\) |
| \(f'(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f}\) | \(\searrow\) | \(TiP(-2|f(-2))\) | \(\nearrow\) |
| \(x\) | \(-2 < x < 0\) | \(0\) | \(0 < x < 2\) |
| \(\frac{1}{8}x\) | \(-\) | \(0\) | \(+\) |
| \((x - 2)\) | \(-\) | \(-\) | \(-\) |
| \((x + 2)\) | \(+\) | \(+\) | \(+\) |
| \(f'(x)\) | \(+\) | \(0\) | \(-\) |
| \(G_{f}\) | \(\nearrow\) | \(HoP(0|f(0))\) | \(\searrow\) |
| \(x\) | \(0 < x < 2\) | \(2\) | \(x > 2\) |
| \(\frac{1}{8}x\) | \(+\) | \(+\) | \(+\) |
| \((x - 2)\) | \(-\) | \(0\) | \(+\) |
| \((x + 2)\) | \(+\) | \(+\) | \(+\) |
| \(f'(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f}\) | \(\searrow\) | \(TiP(2|f(2))\) | \(\nearrow\) |
Lage (\(y\)-Koordinate) der Extrempunkte:
\[f(x) = \frac{1}{32}x^{4} - \frac{1}{4}x^{2} + 1\]
\[\begin{align*}f(-2) &= f(2) \qquad (G_{f} \; \text{achsensymmetrisch zur}\;y\text{-Achse}) \\[0.8em] &= \frac{1}{32} \cdot 2^{4} - \frac{1}{4} \cdot 2^{2} + 1 \\[0.8em] &= \frac{16}{32} - 1 + 1 \\[0.8em] &= \frac{1}{2} \end{align*}\]
\[\Longrightarrow \quad TiP\Big(-2|\textstyle \frac{1}{2}\Big), \; TiP\Big(2|\textstyle \frac{1}{2}\Big)\]
\(f(0) = 1\) (vgl. Teilaufgabe d)
\[\Longrightarrow \quad HoP(0|1)\]
f) Zeichnung von \(G_{f}\) sowie der Tangente \(T\) unter Berücksichtigung der bisherigen Ergebnisse
Bisherige Ergebnisse:
- Symmetrieverhalten: \(G_{f}\) ist achsensymmetrisch zur \(y\)-Achse.
- Verhalten im Unendlichen: \(\lim \limits_{x\,\to\,\pm\infty} f(x) = +\infty\)
- Gleichung der Tangente \(T\): \(y = -\frac{3}{8}x + \frac{37}{32}\)
- Schnittpunkt von \(G_{f}\) mit der \(y\)-Achse: \(S_{y}(0|1)\)
- Extrempunkte: \(TiP\Big(-2|\textstyle \frac{1}{2}\Big), \; TiP\Big(2|\textstyle \frac{1}{2}\Big), \; HoP(0|1)\)
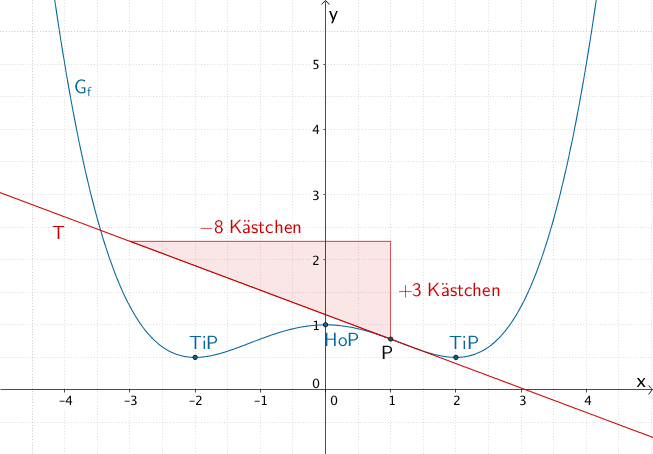
Graph der Funktion \(f \colon x \mapsto \frac{1}{32}x^{4} - \frac{1}{4}x^{2} + 1\) sowie Tangente \(T\) an \(G_{f}\) im Punkt \(P\Big(1|\textstyle \frac{25}{32}\Big)\)


