Skizzieren Sie den Graphen von \(F\) in Abbildung 1.
(2 BE)
Lösung zu Teilaufgabe 4b
\[F(x) = \int_0^x f(t)\,dt\,; \quad D = [-2;2]\]
Aus Teilaufgabe 4a ist bekannt:
\[F(0) = \int_0^0 f(t)\,dt = 0 \quad \Longrightarrow \quad (0|0)\]
\[F(2) = \int_0^2 f(t)\,dt = \frac{\pi}{2} \quad \Longrightarrow \quad \left(2|\frac{\pi}{2}\right)\]
\[F(-2) = \int_0^{-2} f(t)\,dt = -\frac{\pi}{2} \quad \Longrightarrow \quad \left(-2|-\frac{\pi}{2}\right)\]
Die Funktionswerte \(F(-1)\) und \(F(1)\) lassen sich zusätzlich einfach berechnen, indem man den Flächeninhalt eines Viertelkreises bestimmt:
\[F(-1) = \int_0^{-1} f(t)\,dt = -\frac{\pi}{4} \quad \Longrightarrow \quad \left(-1|-\frac{\pi}{4}\right)\]
\[F(1) = \int_0^1 f(t)\,dt = \frac{\pi}{4} \quad \Longrightarrow \quad \left(1|\frac{\pi}{4}\right)\]
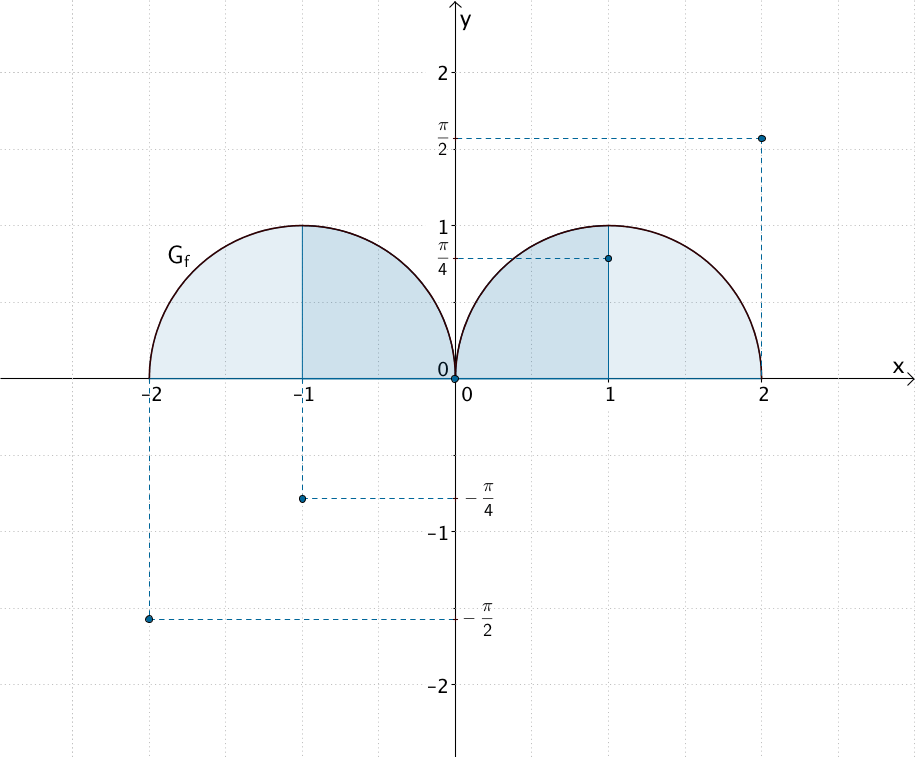
Die bisher errechneten Funktionswerte für die Integralfunktion \(F\) vermitteln den Eindruck, der Graph von \(F\) sei eine Ursprungsgerade.
Dieser Eindruck täuscht!
Weitere Eigenschaften des Graphen der Integralfunktion \(F\)
Betrachtung der Extremstellen von \(G_f\):
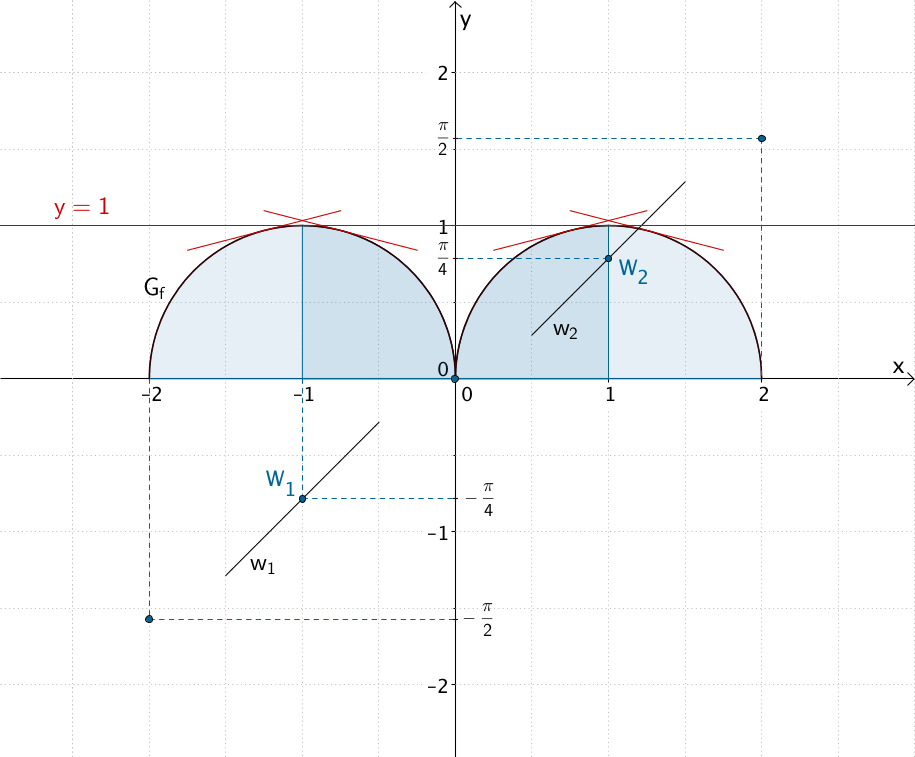
Waagrechte Tangente \(y = 1\) an den Extremstellen \(x_{E_1} = -1\) und \(x_{E_2} = 1\) von \(G_f\), Tangenten in der Umgebung der Extremstellen von \(G_f\)
An den Extremstellen \(x_{E_1} = -1\) und \(x_{E_2} = 1\) hat der Graph von \(f\) eine waagrechte Tangente mit der Gleichung \(y = 1\). Die erste Ableitung \(f'(x)\) beschreibt die Steigung einer Tangente an \(G_f\). Also gilt:
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[f'(-1) = 0\,; \quad f'(1) = 0\]
Daraus folgt nach dem Hauptsatz der Differential- und Integralrechnung:
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[f'(-1) = F''(-1) = 0\,; \quad f'(1) = F''(1) = 0\]
In der Umgebung der Extremstellen \(x_{E_1} = -1\) und \(x_{E_2} = 1\) von \(G_f\) wechselt die Steigung der Tangente an \(G_f\) von positiv nach negativ. Demnach sind die Extremstellen von \(G_f\) die Wendestellen des Graphen der Integralfunktion \(F\).
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
\[\Longrightarrow \quad W_1\,\left(-1|-\frac{\pi}{4}\right)\,,\quad W_2\,\left(1|\frac{\pi}{4}\right)\]
Wendetangente:
Wegen \(f(-1) = 1\) und \(f(1) = 1\) gilt nach dem Hauptsatz der Differential- und Integralrechnung:
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[f(-1) = F'(-1) = 1\,; \quad f(1) = F'(1) = 1\]
Damit folgt für Steigung der Wendetangenten \(w_1\) und \(w_2\):
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[m_{w_1} = F'(-1) = 1\,; \quad m_{w_2} = F'(1) = 1\]
Wichtig:
Die Extremstellen des Graphen der Ableitung \(f'\) einer Funktion \(f\) sind immer die Wendestellen des Graphen einer Funktion \(f\). An den Wendestellen ist die Steigung des Graphen einer Funktion \(f\) (Steigung der Wendetangente) maximal oder minimal. Das Krümmungsverhalten des Graphen einer Funktion \(f\) ändert sich an den Wendestellen.
Betrachtung der Graphenkrümmung von \(G_F\):
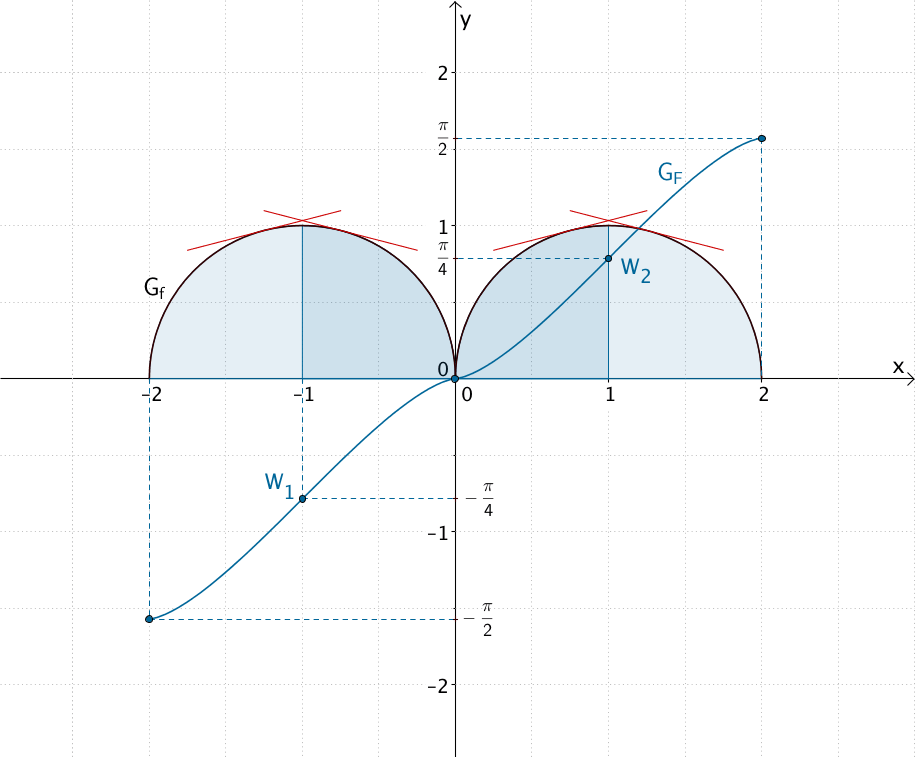
Graph der Integralfunktion \(F\) mit den Wendepunkten \(W_1\) und \(W_2\)
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
Für \(x \in \; ]-2;-1[\) ist die Steigung einer Tangente an \(G_f\) positiv.
\(\Longrightarrow \quad f'(x) = F''(x) > 0\) für \(x \in \; ]-2;-1[\)
\(\Longrightarrow \quad G_F\) ist im Intervall \(]-2;-1[\) linksgekrümmt.
Für \(x \in \; ]-1;0[\) ist die Steigung einer Tangente an \(G_f\) negativ.
\(\Longrightarrow \quad f'(x) = F''(x) < 0\) für \(x \in \; ]-1;0[\)
\(\Longrightarrow \quad G_F\) ist im Intervall \(]-1;0[\) rechtsgekrümmt.
Für \(x \in \; ]0;1[\) ist die Steigung einer Tangente an \(G_f\) positiv.
\(\Longrightarrow \quad f'(x) = F''(x) > 0\) für \(x \in \; ]0;1[\)
\(\Longrightarrow \quad G_F\) ist im Intervall \(]0;1[\) linksgekrümmt.
Für \(x \in \; ]1;2[\) ist die Steigung einer Tangente an \(G_f\) negativ.
\(\Longrightarrow \quad f'(x) = F''(x) < 0\) für \(x \in \; ]1;2[\)
\(\Longrightarrow \quad G_F\) ist im Intervall \(]1;2[\) rechtsgekrümmt.
Betrachtung der Nullstellen der Funktion \(f\):
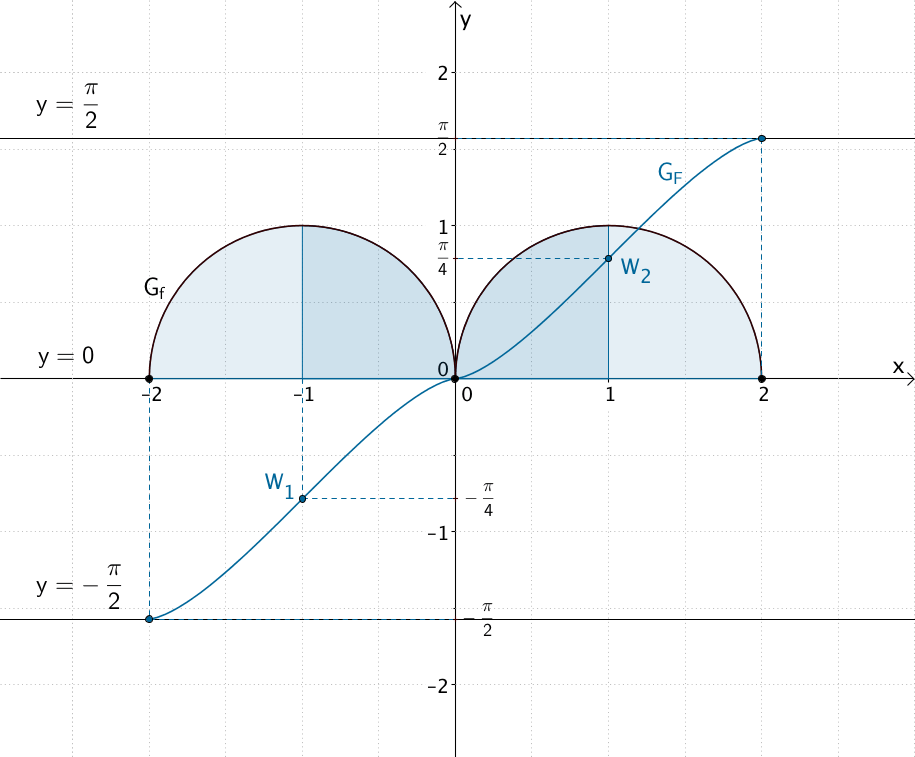
Nullstellen des Graphen der Funktion \(f\) und waagrechte Tangenten des Graphen der Integralfunktion \(F\)
Die Nullstellen der Funktion \(f\) sind \(x_{N_1} = -2\), \(x_{N_2} = 0\) und \(x_{N_3} = 2\).
Nach dem Hauptsatz der Differential- und Integralrechnung gilt:
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[f(-2) = F'(-2) = 0\]
\[f(0) = F'(0) = 0\]
\[f(2) = F'(2) = 0\]
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Demnach hat der Graph der Integralfunktion \(F\) in den Punkten \(\displaystyle \left(-2|-\frac{\pi}{2}\right)\), \((0|0)\) und \(\displaystyle \left(2|\frac{\pi}{2}\right)\) waagrechte Tangenten mit den Gleichungen \(\displaystyle y = -\frac{\pi}{2}\), \(y = 0\) und \(\displaystyle y = \frac{\pi}{2}\).
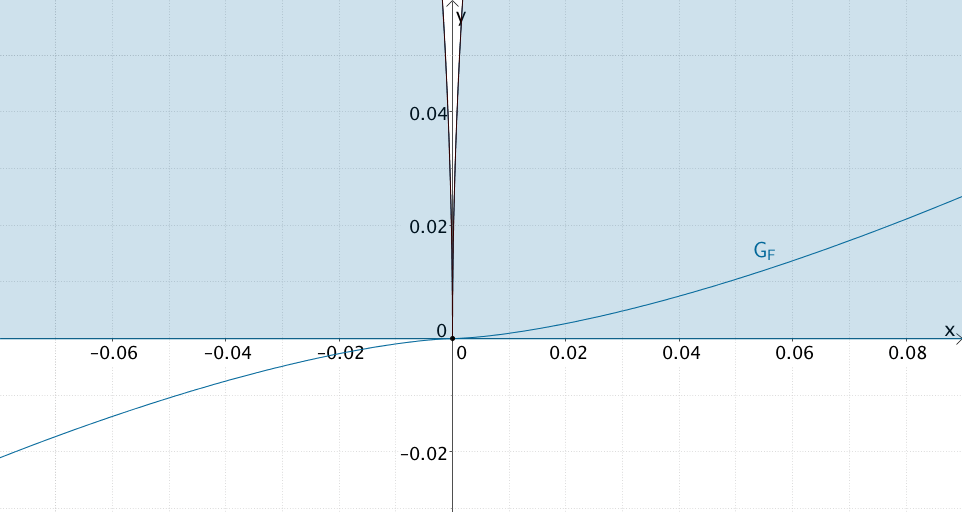
10-fache Vergrößerung: Verhalten des Graphen der Integralfunktion \(F\) in der Umgebung der Nullstelle \(x = 0\).
Anmerkung:
Die Vergrößerung verdeutlicht, wie schwierig es ist, den Graphen der Integralfunktion \(F\) an den Nullstellen der Funktion \(f\) zu skizzieren. Die Aufgabenstellung verlangt lediglich nach einer Skizze von \(G_f\). Eine Begründung dafür ist nicht notwendig. Bei 2 BE (Bewertungseinheiten) soll der Graph von \(F\) vor allem keine Gerade sein, sondern in den Intervallen \([-2;0]\) und \([0;2]\) jeweils einem S-förmigen Verlauf folgen.


