Vektorprodukt
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
Anwendungen des Vektorprodukts
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) lässt sich geometrisch als die Maßzahl des Flächeninhalts des Parallelogramms deuten, welches die Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) aufspannen (vgl. Abbildung).

Flächeninhalt eines von zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) aufgespannten Parallelogramms
\[A_{\text{Parallelogramm}} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} = \vert \overrightarrow{a} \times \overrightarrow{b} \vert \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Flächeninhalt eines Parallelogramms
\[A_{\text{Parallelogramm}} = \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
Flächeninhalt eines Dreiecks (vgl. Merkhilfe)
\[A_{\text{Dreieck}} = \frac{1}{2} \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
Mithilfe des Vektorprodukts kann ein zu zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) senkrecht stehender Vektor \(\overrightarrow{c}\) ermittelt werden (beispielsweise der Normalenvektor einer Ebene, vgl. Abiturskript - 2.2.4 Umwandlung: Parameterform - Normalenform).
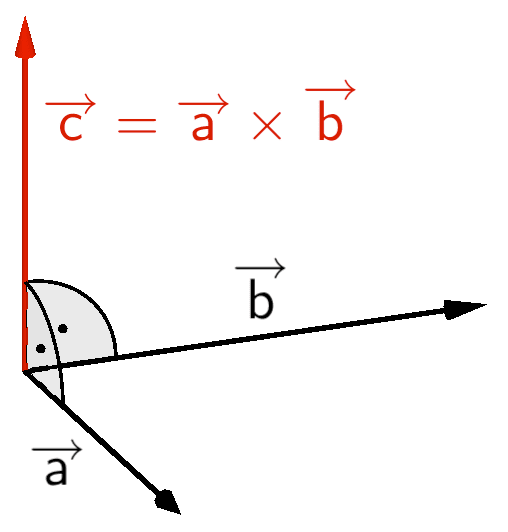
Orthogonaler (senkrechter) Vektor zu zwei (linear unabhängigen) Vektoren
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Beispielaufgabe
Gegeben seien die Punkte \(A(7|1|2)\), \(B(5|5|2)\), \(C(-2|7|4)\) und \(D(0|0|4{,}5)\), welche das unregelmäßige Viereck \(ABCD\) festlegen.
Berechnen Sie den Flächeninhalt \(A\) des Vierecks \(ABCD\).
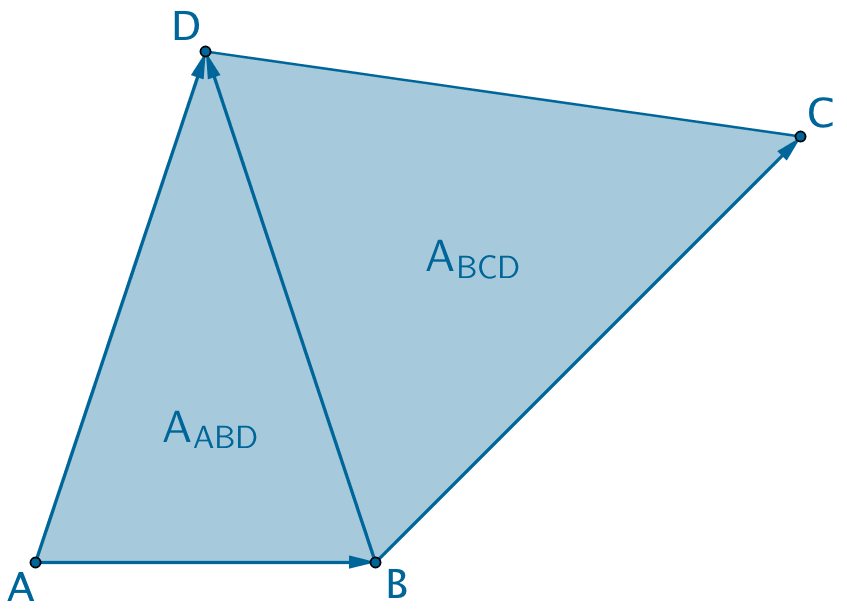
Planskizze: Unregelmäßiges Viereck \(ABCD\)
Ein beliebiges unregelmäßiges Viereck \(ABCD\) lässt sich beispielsweise entlang der Strecke \([BD]\) in zwei Dreiecke zerlegen, deren Flächeninhalte sich mithilfe des Vektorprodukts berechnen lassen.
\[\begin{align*}A &= A_{ABD} + A_{BCD} \\[0.8em] &= \frac{1}{2} \cdot \vert \overrightarrow{AB} \times \overrightarrow{AD} \vert + \frac{1}{2} \cdot \vert \overrightarrow{BC} \times \overrightarrow{BD} \vert\end{align*}\]
Verbindungsvektoren \(\overrightarrow{AB}\), \(\overrightarrow{AD}\), \(\overrightarrow{BC}\) und \(\overrightarrow{BD}\) berechnen:
\(A(7/1/2)\), \(B(5|5|2)\), \(C(-2|7|4)\), \(D(0|0|4{,}5)\)
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 5 \\ 5 \\ 2 \end{pmatrix} - \begin{pmatrix} 7 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} -2 \\ 4 \\ 0 \end{pmatrix}\]
\[\overrightarrow{AD} = \overrightarrow{D} - \overrightarrow{A} = \begin{pmatrix} 0 \\ 0 \\ 4{,}5 \end{pmatrix} - \begin{pmatrix} 7 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} -7 \\ -1 \\ 2{,}5 \end{pmatrix}\]
\[\overrightarrow{BC} = \overrightarrow{C} - \overrightarrow{B} = \begin{pmatrix} -2 \\ 7 \\ 4 \end{pmatrix} - \begin{pmatrix} 5 \\ 5 \\ 2 \end{pmatrix} = \begin{pmatrix} -7 \\ 2 \\ 2 \end{pmatrix}\]
\[\overrightarrow{BD} = \overrightarrow{D} - \overrightarrow{B} = \begin{pmatrix} 0 \\ 0 \\ 4{,}5 \end{pmatrix} - \begin{pmatrix} 5 \\ 5 \\ 2 \end{pmatrix} = \begin{pmatrix} -5 \\ -5 \\ 2{,}5 \end{pmatrix}\]
Flächeninhalt \(A\) des Vierecks \(ABCD\) berechnen:
\[\begin{align*}A \enspace = \qquad &A_{ABD} + A_{BCD} \\[0.8em] = \qquad &\frac{1}{2} \cdot \vert \overrightarrow{AB} \times \overrightarrow{AD} \vert + \frac{1}{2} \cdot \vert \overrightarrow{BC} \times \overrightarrow{BD} \vert \\[0.8em] = \qquad &\frac{1}{2} \cdot \left| \begin{pmatrix} -2 \\ 4 \\ 0 \end{pmatrix} \times \begin{pmatrix} -7 \\ -1 \\ 2{,}5 \end{pmatrix} \right| + \frac{1}{2} \cdot \left| \begin{pmatrix} -7 \\ 2 \\ 2 \end{pmatrix} \times \begin{pmatrix} -5 \\ -5 \\ 2{,}5 \end{pmatrix} \right| \\[0.8em] = \qquad &\frac{1}{2} \cdot \left| \begin{pmatrix} 4 & \cdot & 2{,}5 & - & 0 & \cdot & (-1) \\ 0 & \cdot & (-7) & - & (-2) & \cdot & 2{,}5 \\ (-2) & \cdot & (-1) & - & 4 & \cdot & (-7) \end{pmatrix} \right| \\[0.8em] + \enspace &\frac{1}{2} \cdot \left| \begin{pmatrix} 2 & \cdot & 2{,}5 & - & 2 & \cdot & (-5) \\ 2 & \cdot & (-5) & - & (-7) & \cdot & 2{,}5 \\ (-7) & \cdot & (-5) & - & 2 & \cdot & (-5) \end{pmatrix} \right| \\[0.8em] = \qquad &\frac{1}{2} \cdot \left| \begin{pmatrix} 10 \\ 5 \\ 30 \end{pmatrix} \right| + \frac{1}{2} \cdot \left| \begin{pmatrix} 15 \\ 7{,}5 \\ 45 \end{pmatrix} \right| \\[0.8em] = \qquad &\frac{1}{2} \cdot \sqrt{10^{2} + 5^{2} + 30^{2}} + \frac{1}{2} \cdot \sqrt{15^{2} + 7{,}5^{2} + 45^{2}} \\[0.8em] = \qquad &\frac{1}{2} \cdot \sqrt{1025} + \frac{1}{2} \cdot \sqrt{2306{,}25} \\[0.8em] = \qquad &\frac{5}{2}\sqrt{41} + \frac{15}{4}\sqrt{41} \\[0.8em] = \qquad &\frac{25}{4}\sqrt{41} \\[0.8em] \approx \qquad &40{,}02 \end{align*}\]
Der Flächeninhalt \(A\) des Vierecks \(ABCD\) beträgt ca. 40,02 FE (Flächeneinheiten).


