Gegeben sind die in \(\mathbb R\) definierten Funktionen \(g \colon x \mapsto e^{-x}\) und \(h \colon x \mapsto x^3\).
Veranschaulichen Sie durch eine Skizze, dass die Graphen von \(g\) und \(h\) genau einen Schnittpunkt haben.
(2 BE)
Lösung zu Teilaufgabe 3a
\[\begin{align*}g(x) &= e^{-x} & & D = \mathbb R \\ h(x) &= x^3 & & D = \mathbb R \end{align*}\]
Die Graphen der Funktionen \(g\) und \(h\) lassen sich in Kenntnis einiger charakteristischer Eigenschaften gut skizzieren.
Eigenschaften der Funktion \(g\,\):
\[g(0) = e^{-0} = 1 \quad \Longrightarrow \quad S_y\,(0|1)\]
Spiegeln von Funktionsgraphen
Spiegelung an der \(x\)-Achse: \(g(x) = -f(x)\)
Spiegelung an der \(y\)-Achse: \(h(x) = f(-x)\)
Der Graph der Funktion \(g(x) = e^{-x}\) geht aus dem Graphen der Funktion \(f(x) = e^x\) durch Spiegelung an der \(y\)-Achse hervor.
\[\lim \limits_{x \, \to \, - \infty} g(x) = \lim \limits_{x \, \to \, - \infty} e^{-x} = + \infty\]
\[\lim \limits_{x \, \to \, + \infty} g(x) = \lim \limits_{x \, \to \, + \infty} e^{-x} = \lim \limits_{x \, \to \, + \infty} \; \frac{1}{e^x} = 0\]
Eigenschaften der Funktion \(h\,\):
\(h(0) = 0^3 = 0 \quad \Longrightarrow \quad\) dreifache Nullstelle \(N\,(0|0)\)
\[h(1) = 1^3 = 1\,; \quad h(-1) = (-1)^3 = -1\]
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
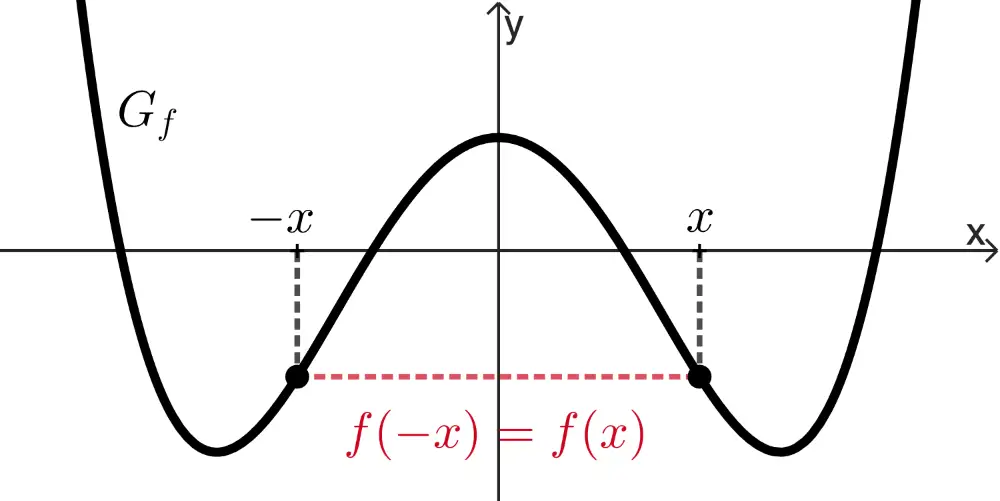
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
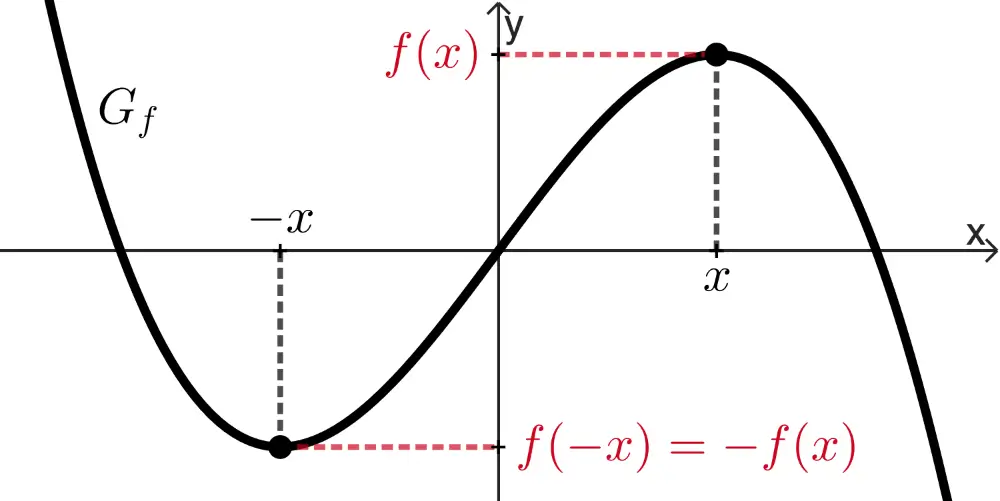
\(h(-x) = (-x)^3 = -x^3 = -h(x) \quad \Longrightarrow \quad G_h\) ist punktsymmetrisch zum Ursprung.
\[\lim \limits_{x \, \to \, - \infty} h(x) = \lim \limits_{x \, \to \, - \infty} x^3 = - \infty\]
\[\lim \limits_{x \, \to \, + \infty} h(x) = \lim \limits_{x \, \to \, + \infty} x^3 = + \infty\]
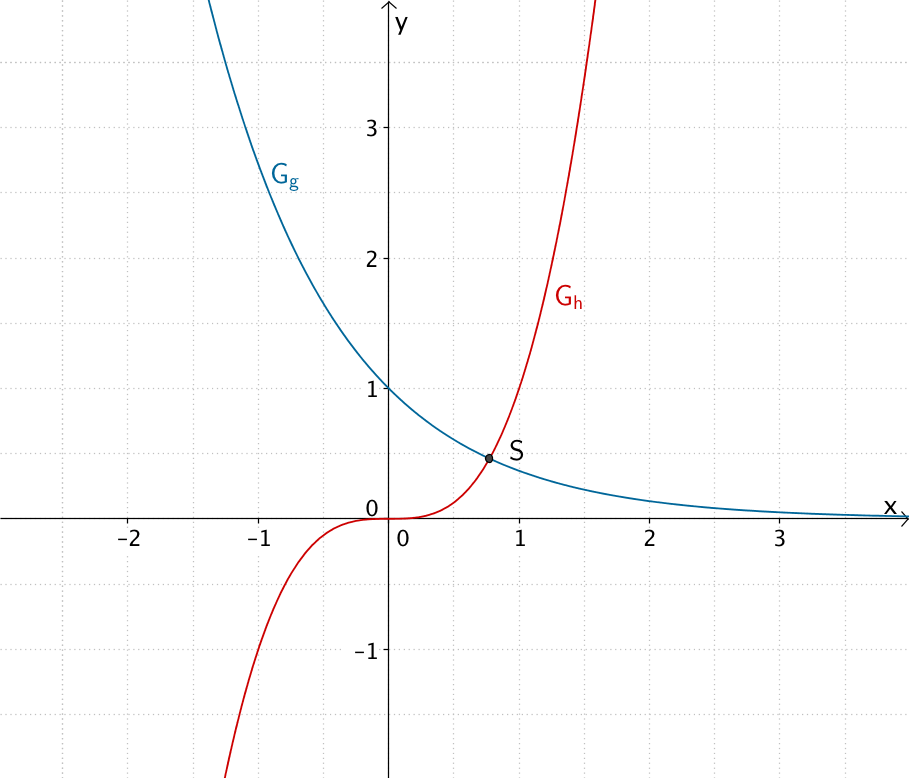
Graphen der Funktionen \(g\) und \(h\), Schnittpunkt \(S\) der Funktionsgraphen


