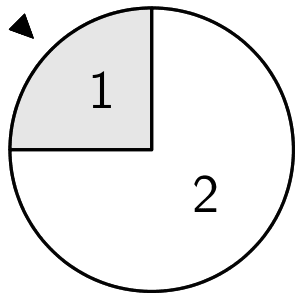
Ein Glücksrad ist in zwei Sektoren unterteilt. Ein Sektor ist mit einer Eins und der andere Sektor mit einer Zwei beschriftet (vgl. Abbildung). Für ein Spiel wird das Glücksrad solange gedreht, bis zum ersten mal die Eins erscheint, jedoch höchstens dreimal. Erscheint die Eins bei der ersten Drehung, erhält der Spieler 5 €, erscheint die Eins bei der zweiten Drehung, erhält er 1 €..
a) Berechnen Sie den Einsatz des Spiels, sodass das Spiel „fair" ist.
b) Der Einsatz des Spiels beträgt nun 1 €. Wie sind die Öffnungswinkel der Sektoren des Glücksrads zu wählen, damit das Spiel „fair" ist?
a) Einsatz des Spiels, sodass das Spiel „fair" ist
Ein Spiel heißt „fair", wenn der Erwartungswert des Gewinns für jeden Spieler \(0\) ist.
Um den Einsatz des „fairen" Spiels zu berechnen, gibt es zwei Möglichkeiten:
Einmal kann der Erwartungswert des Auszahlungsbetrags pro Spiel betrachtet werden, um von diesem auf den Einsatz pro Spiel zu schließen.
Oder es wird der Erwartungswert des Gewinns pro Spiel unter Berücksichtigung eines unbekannten Einsatzes ermittelt. Da der Erwartungswert des Gewinns gleich Null sein muss, lässt sich auf diese Weise der Einsatz berechnen.
1. Möglichkeit: Auszahlungsbetrag betrachten
Es sei \(X\) die Zufallsgröße, welche der Anzahl der Drehungen des Glücksrads einen Auszahlungsbetrag in Euro zuordnet.
Veranschaulichung des Spiels als Baumdiagramm:
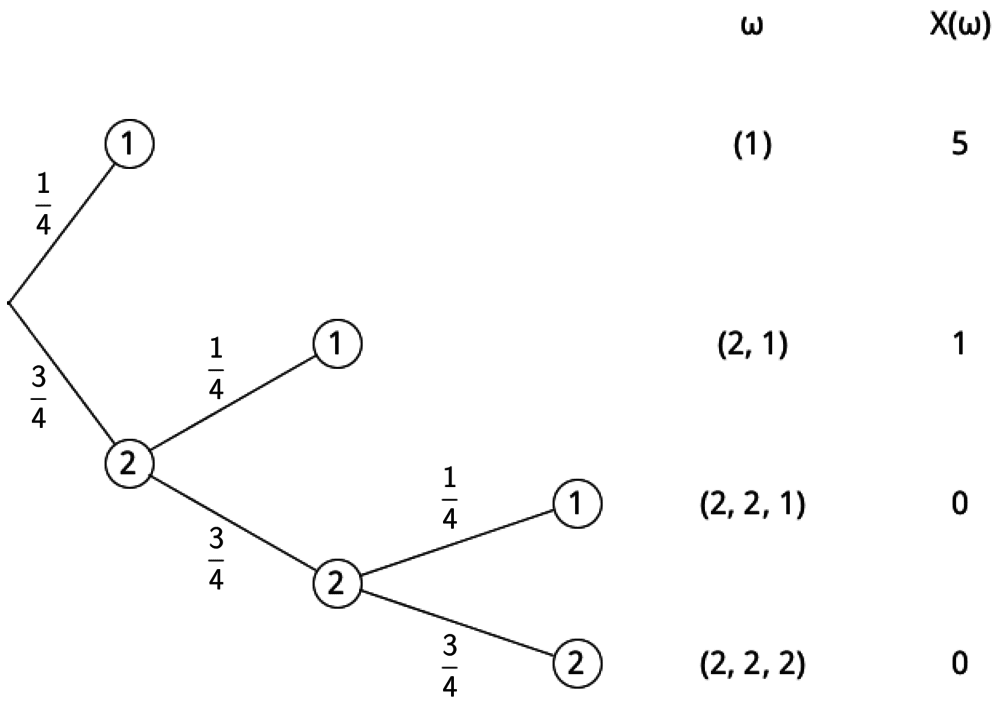
Entsprechend der Größe der Sektoren des Glücksrads (vgl. Abbildung Angabe), erscheint die Eins mit der Wahrscheinlichkeit \(\frac{1}{4}\) und die Zwei mit der Wahrscheinlichkeit \(\frac{3}{4}\).
Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) (Auszahlungsbetrag in Euro):
\[P(X = 5) = P(1) = \frac{1}{4}\]
Die Wahrscheinlichkeiten \(P(X = 1)\) und \(P(X = 0)\) lassen sich mithilfe der Pfadregeln berechnen.
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Nach der ersten Pfadregel gilt:
\[P(X = 1) = P(2,1) = \frac{3}{4} \cdot \frac{1}{4} = \frac{3}{16}\]
Nach der ersten und zweiten Pfadregel gilt:
\[\begin{align*}P(X = 0) &= P(2,2,1) + P(2,2,2) \\[0.8em] &= \frac{3}{4} \cdot \frac{3}{4} \cdot \frac{1}{4} + \frac{3}{4} \cdot \frac{3}{4} \cdot \frac{3}{4} \\[0.8em] &= \frac{9}{64} + \frac{27}{64} \\[0.8em] &= \frac{36}{64} \\[0.8em] &= \frac{9}{16} \end{align*}\]
Anmerkung:
Da auf die Anzahl der Drehungen geachtet wird und das Glücksrad maximal dreimal gedreht wird, ist es unerheblich, ob bei der dritten Drehung die Eins oder die Zwei erscheint. Die Wahrscheinlichkeit dafür, dass bei der dritten Drehung die Eins oder die Zwei erscheint ist also \(1\). Somit kann die Wahrscheinlichkeit \(P(X = 0)\) auch wie folgt nur mithilfe der ersten Pfadregel berechnet werden:
\[P(X = 0) = P(2,2) = \frac{3}{4} \cdot \frac{3}{4} ( \cdot 1) = \frac{9}{16}\]
Tabelle der Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) (optional):
| \(X = x_{i}\) | \(0\) | \(1\) | \(5\) |
| \(P(X = x_{i})\) | \(\dfrac{9}{16}\) | \(\dfrac{3}{16}\) | \(\dfrac{1}{4}\) |
Erwartungswert der Zufallsgröße \(X\) (des Auszahlungsbetrags) berechnen:
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) der Zufallsgröße \(\boldsymbol{X}\) (vgl. Merkhilfe)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot p_{i} \\[0.8em] &= x_{1} \cdot p_{1} + x_{2} \cdot p_{2} \,+\, ... \,+\, x_{n} \cdot p_{n} \end{align*}\]
Der Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(X\) gibt den Mittelwert der Zufallsgröße an, der bei oftmaliger Wiederholung eines Zufallsexperiments zu erwarten ist.
\[\begin{align*}E(X) &= x_{1} \cdot P(X = x_{1}) + x_{2} \cdot P(X = x_{2}) + x_{3} \cdot P(X = x_{3}) \\[0.8em] &= 0 \cdot \frac{9}{16} + 1 \cdot \frac{3}{16} + 5 \cdot \frac{1}{4} \\[0.8em] &= \frac{23}{16} \\[0.8em] &= 1{,}4375 \end{align*}\]
Im Mittel erhält ein Spieler pro Spiel einen Auszahlungsbetrag in Höhe von ca. 1,44 Euro.
Damit das Spiel „fair" ist, muss ein Spieler also pro Spiel einen Einsatz in Höhe von ca. 1,44 Euro zahlen.
2. Möglichkeit: Gewinn betrachten
Es sei \(G\) die Zufallsgröße, welche der Anzahl der Drehungen des Glücksrads einen Auszahlungsbetrag in Euro zuordnet.
Es gilt: \(\text{Gewinn} = \text{Auszahlungsbetrag} - \text{Einsatz}\)
Es sei \(x\) der zu bestimmende Einsatz pro Spiel.
Damit ergibt sich folgende Wahrscheinlichkeitsverteiling der Zufallsgröße \(G\):
| \(G = g_{i}\) | \(0 - x\) | \(1 - x\) | \(5 - x\) |
| \(P(G = g_{i})\) | \(\dfrac{9}{16}\) | \(\dfrac{3}{16}\) | \(\dfrac{1}{4}\) |
Erwartungswert der Zufallsgröße \(G\) (des Gewinns) in Abhängigkeit des Einsatzes \(x\) formulieren:
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) der Zufallsgröße \(\boldsymbol{X}\) (vgl. Merkhilfe)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot p_{i} \\[0.8em] &= x_{1} \cdot p_{1} + x_{2} \cdot p_{2} \,+\, ... \,+\, x_{n} \cdot p_{n} \end{align*}\]
Der Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(X\) gibt den Mittelwert der Zufallsgröße an, der bei oftmaliger Wiederholung eines Zufallsexperiments zu erwarten ist.
\[\begin{align*}E(G) &= g_{1} \cdot P(G = g_{1}) + g_{2} \cdot P(G = g_{2}) + g_{3} \cdot P(G = g_{3}) \\[0.8em] &= (0 - x) \cdot \frac{9}{16} + (1 - x) \cdot \frac{3}{16} + (5 - x) \cdot \frac{1}{4} \\[0.8em] &= -\frac{9}{16}x + \frac{3}{16} - \frac{3}{16}x + \frac{5}{4} - \frac{1}{x}x \\[0.8em] &= -x + \frac{23}{16} \end{align*}\]
Mit der Bedingung \(E(G) = 0\) für ein „faires" Spiel folgt:
\[\begin{align*} E(G) &= 0 \\[0.8em] -x + \frac{23}{16} &= 0 &&| + x \\[0.8em] \frac{23}{16} &= x \\[0.8em] 1{,}4375 &= x \end{align*}\]
Damit das Spiel „fair" ist, muss ein Spieler pro Spiel einen Einsatz in Höhe von ca. 1,44 Euro zahlen.
b) Öffnungswinkel der Sektoren des Glücksrads, damit das Spiel bei einem Einsatz von 1 € „fair" ist
Es sei \(G\) die Zufallsgröße, welche der Anzahl der Drehungen des Glücksrads einen Auszahlungsbetrag in Euro zuordnet.
Beispielsweise wählt man \(p\) für die Wahrscheinlichkeit mit der die Eins erscheint und \(1 - p\) für die Wahrscheinlichkeit, mit der die Zwei erscheint.
Die Bedingung für ein „faires" Spiel lautet: \(E(G) = 0\). Damit lässt sich \(p\) berechnen und letztendlich auch der Öffnungswinkel der Sektoren des Glücksrads.
Bei einem Einsatz von 1 € kann die Zufallsgröße \(G\) (Gewinn) die Werte \(g_{1} = -1\), \(g_{2} = 0\) und \(g_{3} = 4\) annehmen.
Veranschaulichung als Baumdiagramm:
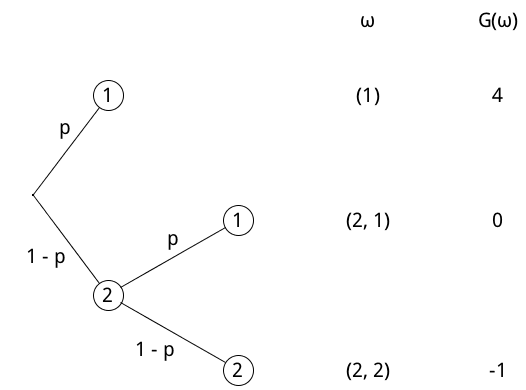
Wahrscheinlichkeitsverteilung der Zufallsgröße \(G\) in Abhängigkeit von \(p\) beschreiben:
\[P(G = 4) = P(1) = p\]
Nach der ersten Pfadregel gilt:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[P(G = 0) = P(2,1) = (1 - p) \cdot p\]
\[P(G = -1) = P(2,2) = (1 - p)^{2}\]
| \(G = g_{i}\) | \(-1\) | \(0\) | \(4\) |
| \(P(G = g_{i})\) | \((1 - p)^{2}\) | \((1 - p) \cdot p\) | \(p\) |
Erwartungswert der Zufallsgröße \(G\) (des Gewinns) in Abhängigkeit von \(p\) formulieren:
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) der Zufallsgröße \(\boldsymbol{X}\) (vgl. Merkhilfe)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot p_{i} \\[0.8em] &= x_{1} \cdot p_{1} + x_{2} \cdot p_{2} \,+\, ... \,+\, x_{n} \cdot p_{n} \end{align*}\]
Der Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(X\) gibt den Mittelwert der Zufallsgröße an, der bei oftmaliger Wiederholung eines Zufallsexperiments zu erwarten ist.
\[\begin{align*}E(G) &= g_{1} \cdot P(G = g_{1}) + g_{2} \cdot P(G = g_{2}) + g_{3} \cdot P(G = g_{3}) \\[0.8em] &= (-1) \cdot (1 - p)^{2} + 0 \cdot (1 - p) \cdot p + 4 \cdot p \\[0.8em] &= 4p - (1 - 2p + p^{2}) \\[0.8em] &= -p^{2} + 6p - 1 \end{align*}\]
Mit \(E(G) = 0\) ergibt sich eine quadratische Gleichung. Es wird die Lösungsformel für quadratische Gleichungen angewedet.
\[\begin{align*}E(G) &= 0 \\[0.8em] -p^{2} + 6p - 1 &= 0 &&(0 \leq p \leq 1) \end{align*}\]
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*} p_{1,2} &= \frac{-6 \pm \sqrt{6^{2} - 4 \cdot (-1) \cdot (-1)}}{2 \cdot (-1)} \\[0.8em] &= \frac{-6 \pm \sqrt{32}}{-2} \\[0.8em] &= 3 \pm 2\sqrt{2} \end{align*}\]
\[\left(p_{1} = 3 + 2\sqrt{2} \approx 5{,}8\right)\]
\[p_{2} = 3 - 2\sqrt{2} \approx 0{,}17\]
Damit das Spiel bei einem Einsatz von 1 Euro „fair" ist, muss die Wahrscheinlichkeit dafür, dass beim Drehen des Glücksrads die Eins erscheint, ungefähr 0,17 betragen.
Öffnungswinkel der Sektoren berechnen:
\[0{,}17 \cdot 360^{\circ} = 61{,}2^{\circ}\]
\[360^{\circ} - 61{,}2^{\circ} = 298{,}8^{\circ}\]
Damit das Spiel bei einem Einsatz von 1 Euro „fair" ist, muss der Öffnungswinkel des Sektors mit der Eins 61,2° betragen. Der Öffnungswinkel des Sektors mit der Zwei ergibt sich somit zu 298,8°.

