Die Abbildung zeigt den Graphen der in \(\mathbb R\) definierten Funktion \(f\).
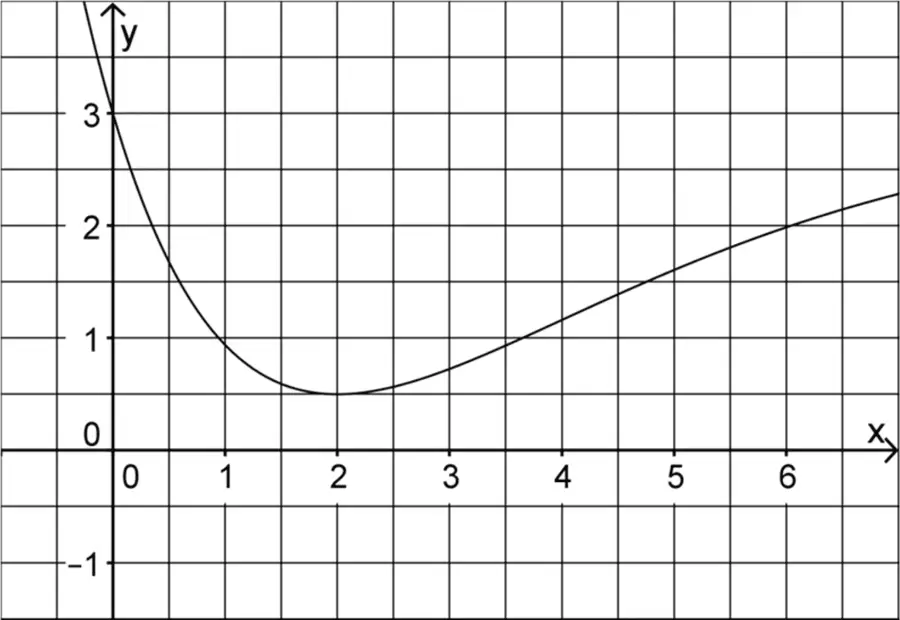
Bestimmen Sie mithilfe der Abbildung einen Näherungswert für \(\displaystyle \int_{3}^{5} f(x) \,dx\).
(2 BE)
Lösung zu Teilaufgabe 5a
Näherungsweise Integration
![Flächeninhalt A, den der Graph der Funktion f im Intervall [3;5] mit der x-Achse einschließt. Flächeninhalt A, den der Graph der Funktion f im Intervall [3;5] mit der x-Achse einschließt.](/images/stories/B2016_PT_A_A_1/B2016_PT_A_A_1_5a_1.png)
Der Wert des bestimmten Integrals \(\displaystyle \int_{3}^{5} f(x)\,dx\) ist gleich der Maßzahl des Flächeninhalts \(A\) des Flächenstücks, das der Graph der Funktion \(f\) für \(x \in [3;5]\) mit der \(x\)-Achse einschließt.
Der Flächeninhalt \(A\) lässt sich näherungsweise berechnen, indem man das Flächenstück mithilfe einer geeigneten geometrischen Figur annähert oder auf die Methode „Kästchen zählen" zurückgreift.
1. Lösungsansatz: Flächeninhalt eines Trapezes
![Annäherung des Flächenstücks, das der Graph der Funktion f im Intervall [3;5] mit der x-Achse einschließt, durch das Trapez ABCD Annäherung des Flächenstücks, das der Graph der Funktion f im Intervall [3;5] mit der x-Achse einschließt, durch das Trapez ABCD](/images/stories/B2016_PT_A_A_1/B2016_PT_A_A_1_5a_2.png)
Das Trapez \(ABCD\) ersetzt näherungsweise das Flächenstück, das \(G_{f}\) für \(x \in [3;5]\) mit der \(x\)-Achse einschließt.
\(A_{\text{Trapez}} = \dfrac{a + c}{2} \cdot h\)
(vgl. Merkhilfe, wobei \(a, c\) die Längen der parallelen Grundlinien des Trapezes sind und \(h\) die Höhe des Trapezes ist.)
Im Rahmen der Ablesegenauigkeit entnimmt man der Abbildung die Längen der parallelen Grundlinien \([BC]\) und \([DA]\) des Trapezes \(ABCD\).
\[\overline{BC} = 1{.}6 \pm 0{,}1\]
\[\overline{DA} = 0{,}7 \pm 0{,}1\]
Höhe \(h\) des Trapezes \(ABCD\):
\[h = \overline{AB} = 5 - 3 = 2\]
Damit lässt sich der Wert des Integrals \(\displaystyle \int_{3}^{5} f(x) \, dx\) näherungsweise wie folgt berechnen:
\[\begin{align*} \int_{3}^{5} f(x) \, dx &= A \\[0.8em] &\approx A_{ABCD} \\[0.8em] &= \frac{\overline{BC} + \overline{DA}}{2} \cdot \overline{AB} \\[0.8em] &= \frac{1{,}6 + 0{,}7}{2} \cdot 2 \\[0.8em] &= 2{,}3 \end{align*}\]
2. Lösungsansatz: „Kästchen zählen"
![Unterteilung des Flächenstücks, das der Graph von f i, Intervall [3;5] mit der x-Achse einschließt in „Kästchen" Unterteilung des Flächenstücks, das der Graph von f i, Intervall [3;5] mit der x-Achse einschließt in „Kästchen"](/images/stories/B2016_PT_A_A_1/B2016_PT_A_A_1_5a_3.png)
Im Rahmen der Ablesegenauigkeit lässt sich das Flächenstück, das \(G_{f}\) für \(x \in [3;5]\) mit der \(x\)-Achse einschließt, in ca. 9,25 quadratische „Kästchen" vom Flächeninhalt 0,25 FE (Flächeneinheiten) unterteilen.
Damit kann der Wert des Integrals \(\displaystyle \int_{3}^{5} f(x) \, dx\) näherungsweise wie folgt berechnen werden:
\[\begin{align*} \int_{3}^{5} f(x) \, dx &= A \\[0.8em] &\approx 9{,}25 \cdot 0{,}25 \\[0.8em] &\approx 2{,}3 \end{align*}\]


