Die Funktionsgleichung von \(g\) hat also die Form III. Geben Sie den passenden Wert von \(k\) an.
(1 BE)
Lösung zu Teilaufgabe 2f
\[\textsf{III} \enspace y = \frac{2e^{kx}}{e^{kx} + 9}\,; \quad k \in \mathbb R^+\]
Strecken von Funktionsgraphen
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{k}\,\):
\[h(x) = f\left(\textcolor{#0087c1}{\frac{1}{k}} \cdot x \right), \enspace k > 0\]
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{\dfrac{1}{k}}\):
\[h(x) = f(\textcolor{#0087c1}{k} \cdot x), \enspace k > 0\]
Streckung in \(\textcolor{#cc071e}{y}\)-Richtung mit Streckungsfaktor \(\textcolor{#cc071e}{k}\,\):
\[g(x) = \textcolor{#cc071e}{k} \cdot f(x), \enspace k > 0\]
Die Funktionsgleichung von \(g\) der Form III bewirkt eine Stauchung des Graphen von \(f\) (Sonnenblumen der Sorte Alba) in \(x\)-Richtung mit dem Stauchungsfaktor \(k\) (Streckung mit Streckungsfaktor \(\frac{1}{k}\)).
"... so erreichen ... die Sonnenblumen der Sorte Tramonto im Vergleich zu denen der Sorte Alba jede Höhe in der Hälfte der Zeit." (vgl. Angabe Teilaufgabe 2e)
Dieses Verhalten entspricht einer Stauchung des Graphen der Funktion \(f\) um den Faktor \(k = 2\) bzw. einer Streckung um den Faktor \(\frac{1}{2}\).
\[\begin{align*}\Rightarrow \enspace g(x) &= f(2x) \\[0.8em] \frac{2e^{kx}}{e^{kx} + 9} &= \frac{2e^{2x}}{e^{2x} + 9} \end{align*}\]
\[\Rightarrow \enspace k = 2\]
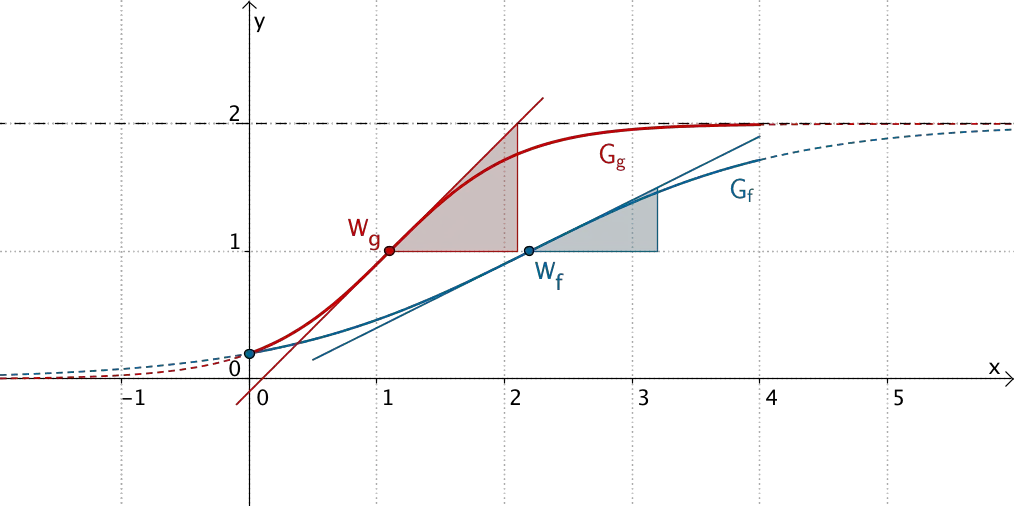
Die Wachstumsrate von Sonnenblumen der Sorte Tramonto (\(\,G_g\,\)) ist doppelt so groß wie die Wachstumsrate von Sonnenblumen der Sorte Alba (\(\,G_f\,\)). Die Abbildung veranschaulicht jeweils die maximale Wachstumsrate (Steigung der Tangente im Wendepunkt).


