Geben Sie in Abhängigkeit von \(c\) die Seitenlängen des Rechtecks \(PQRS\) an und begründen Sie, dass der Flächeninhalt des Rechtecks durch den Term \(A(c) = 4c \cdot e^{-\frac{1}{8}c^2}\) gegeben ist.
(3 BE)
Lösung zu Teilaufgabe 1e
\[f(x) = 2e^{-\frac{1}{8}x^2}; \; D_f = \mathbb R\]
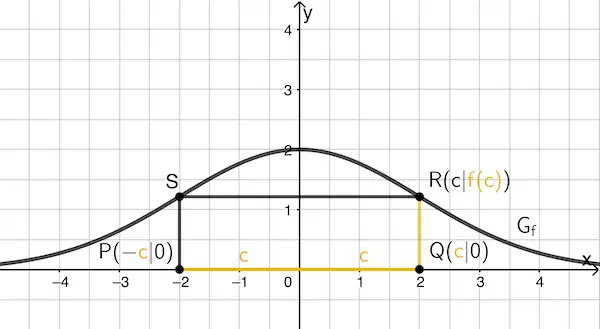 Skizze optional
Skizze optional
Seitenlängen des Rechtecks \(PQRS\): \(\textcolor{#e9b509}{2c}\) und \(\textcolor{#e9b509}{f(c)}\)
\[\begin{align*}A(c) &= \textcolor{#e9b509}{2c} \cdot \textcolor{#e9b509}{f(c)} \\[0.8em] &= 2c \cdot 2e^{-\frac{1}{8}c^2} \\[0.8em] &= 4c \cdot e^{-\frac{1}{8}c^2} \end{align*}\]


