Das Laplace-Gymnasium veranstaltet auf dem Sportplatz ein Fußballturnier für die neuen 5. Klassen.
An dem Turnier nehmen neun Mannschaften teil. Die Mannschaften bestehen jeweils aus Jungen und Mädchen, wobei zwei Drittel aller mitspielenden Kinder männlich sind.
Die drei Spielführerinnen und die sechs Spielführer der Fußballmannschaften stellen sich in einer Reihe für ein Foto auf. Bestimmen Sie die Anzahl der Möglichkeiten für die Aufstellung der neun Kinder, wenn die drei Spielführerinnen nebeneinanderstehen sollen.
(3 BE)
Lösung zu Teilaufgabe 1a
3 Spielführerinnen, 6 Spielführer
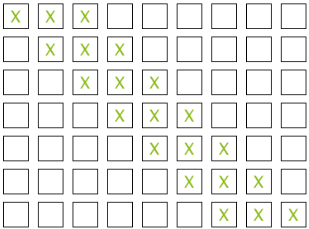
Es gibt 7 Möglichkeiten dafür, dass die 3 Spielführerinnen nebeneinander stehen.
Anmerkung:
Für \(n \geq k\) gibt es \(n - k + 1\) Möglichkeiten, eine Teilmenge von \(k\) Objekten hintereinander und ohne Berücksichtigung deren Reihenfolge (ohne Unterscheidung) auf \(n\) Objekte zu verteilen.
In diesem Fall gibt es \(9 - 3 + 1 = 7\) Möglichkeiten, die 3 Spielführerinnen hintereinander und ohne Berücksichtigung deren Reihenfolge untereinander auf 9 mögliche Plätze zu verteilen.
Anordnung von Objekten
Es gibt \(n!\) Möglichkeiten, \(n\) Objekte in einer Reihe anzuordnen. Eine mögliche Anordung wird als Permutation der \(n\) Objekte bezeichnet.
Es gibt \(\displaystyle \,n \cdot (n - 1)\; \cdot \; ... \; \cdot \; (n - k + 1) = \frac{n!}{(n - k)!}\,\) Möglichkeiten, \(k\) Objekte aus \(n\) verschiedenen Objekten auszuwählen und in einer Reihe anzuordnen.
Es git 3! Möglichkeiten dafür, wie sich die 3 Spielführerinnen untereinander aufstellen.
Es gibt 6! Möglichkeiten dafür, wie sich die 6 Spielführer untereinander aufstellen.
Allgemeines Zählprinzip
Wird ein Zufallsexperiment in \(k\) Stufen durchgeführt und gibt es in der ersten Stufe \(n_{1}\), in der zweiten Stufe \(n_{2}\) und in der \(k\)-ten Stufe \(n_{k}\) mögliche Ergebnisse, so gilt für die Anzahl \(N\) der insgesamt möglichen Ergebnisse:
\[N = n_{1} \cdot n_{2} \cdot \dots \cdot n_{k}\]
Fasst man das Aufstellen der neun Kinder in einer Reihe für ein Foto als dreistufiges Zufallsexperiment auf, so gibt es nach dem Zählprinzip insgesamt
\(\textcolor{#89ba17}{7} \cdot \textcolor{#89ba17}{3!} \cdot \textcolor{#cc071e}{6!} = 30240\) mögliche Aufstellungen.


