Für jeden Wert von \(a\) mit \(a \in \mathbb R^{+}\) ist eine Funktion \(f_{a}\) durch \(f_{a}(x) = \dfrac{1}{a} \cdot x^{3} - x\) mit \(x \in \mathbb R\) gegeben.
Eine der beiden Abbildungen stellt einen Graphen von \(f_{a}\) dar. Geben Sie an, für welche Abbildung dies zutrifft. Begründen Sie Ihre Antwort.
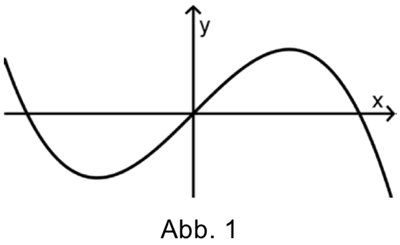
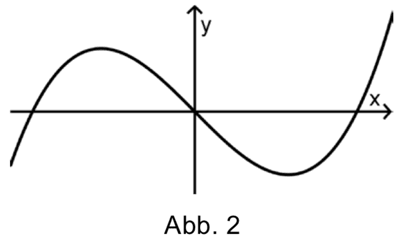
(2 BE)
Lösung zu Teilaufgabe 5a
Abbildung 2 zeigt den Graphen der Funktion \(f_{a}\).
Begründung:
1. Möglichkeit: Verhalten eines Graphen von \(f_{a}\) im Unendlichen betrachten
\[f_{a}(x) = \frac{1}{a} \cdot x^{3} - x; \; a \in \mathbb R^{+}\]
Das Verhalten im Unendlichen eines Graphen der ganzrationalen Funktionenschar \(f_{a}\) wird durch die höchste Potenz \(x^{3}\) zusammen mit dem Leitkoeffizienten \(\dfrac{1}{a}\) bestimmt. Mit \(a \in \mathbb R^{+}\) gilt \(\dfrac{1}{a} > 0\).
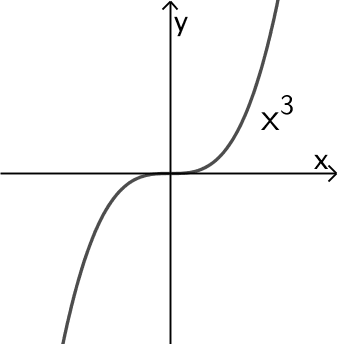

Ein Graph von \(f_{a}\) verhält sich also für \(x \to -\infty\) bzw. \(x \to +\infty\) wie der Graph der Funktion \(x \mapsto x^{3}\).
Somit zeigt Abb. 2 einen Graphen der Funktion \(f_{a}\).
Alternative Begründung durch Grenzwertbestimmung:
\[\lim \limits_{x\,\to\,-\infty} f_{a}(x) = \lim \limits_{x\,\to\,-\infty} \left(\frac{1}{a} \cdot x^{3} - x \right) = \lim \limits_{x\,\to\,-\infty} \underbrace{\frac{1}{a}}_{\large{>\,0}} \cdot \underbrace{x^{3}}_{\to\,-\infty} = -\infty\]
bzw.
\[\lim \limits_{x\,\to\,+\infty} f_{a}(x) = \lim \limits_{x\,\to\,+\infty} \left(\frac{1}{a} \cdot x^{3} - x \right) = \lim \limits_{x\,\to\,+\infty} \underbrace{\frac{1}{a}}_{\large{>\,0}} \cdot \underbrace{x^{3}}_{\to\,+\infty} = +\infty\]
Also zeigt Abb. 2 einen Graphen der Funktion \(f_{a}\).
2. Möglichkeit: Monotonieverhalten eines Graphen von \(f_{a}\) betrachten
Das Monotonieverhalten eines Graphen von \(f_{a}\) an einer betrachteten Stelle \(x_{0}\) lässt sich mithilfe des Vorzeichens von \({f_{a}}'(x_{0})\) beurteilen.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Erste Ableitung \({f_{a}}'\) bilden:
Hierfür wird die Ableitung einer Potenzfunktion sowie die Summen- und die Faktorregel benötigt.
\[f_{a}(x) = \frac{1}{a} \cdot x^{3} - x; \; a \in \mathbb R^{+}\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
vgl. Merkhilfe
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
vgl. Merkhilfe
\[{f_{a}}'(x) = \frac{1}{a} \cdot 3 \cdot x^{2} - 1 = \frac{3}{a}x^{2} - 1\]
Beispielsweise unterscheiden sich die Graphen von Abb. 1 und Abb. 2 im Monotonieverhalten an der Stelle \(x_{0} = 0\).
\[{f_{a}}'(0) = \frac{3}{a} \cdot 0^{2} - 1 = -1 \quad \Longrightarrow \quad {f_{a}}'(0) < 0\]
Somit ist ein Graph von \(f_{a}\) an der Stelle \(x = 0\) streng monoton fallend.
Also zeigt Abb. 2 einen Graphen der Funktion \(f_{a}\).
3. Möglichkeit: Krümmungsverhalten eines Graphen von \(f_{a}\) betrachten
Für die Beurteilung des Krümmungsverhaltens eines Graphen von \(f_{a}\) wird die zweite Ableitung \({f_{a}}''\) benötigt.
\[{f_{a}}'(x) = \frac{3}{a}x^{2} - 1\]
\[{f_{a}}''(x) = \frac{3}{a} \cdot 2 \cdot x - 0 = \frac{6}{a}x\]
Mit \(a \in \mathbb R^{+}\) folgt:
\({f_{a}}''(x) < 0\) für \(x < 0\) und \({f_{a}}''(x) > 0\) für \(x > 0\)
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
Somit ist ein Graph von \(f_{a}\) für \(x < 0\) rechtsgekrümmt und für \(x > 0\) linksgekrümmt.
Also zeigt Abb. 2 einen Graphen der Funktion \(f_{a}\).

