Aufgabe 1

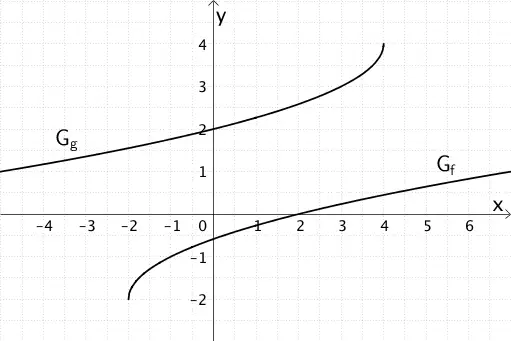
Die Abbildung zeigt je einen Ausschnitt des Graphen \(G_{f}\) der Funktion \(f \colon x \mapsto \sqrt{x + 2} - 2\) und des Graphen \(G_{g}\) der Funktion \(g \colon x \mapsto -\sqrt{4 - x} + 4\).

a) Beschreiben Sie schrittweise wie der Graph \(G_{f}\) und der Graph \(G_{g}\) jeweils aus dem Graphen der Funktion \(x \mapsto \sqrt{x}\) hervorgeht und bestimmen Sie jeweils die maximale Definitionsmenge der Funktionen \(f\) und \(g\) durch Rechnung.

Betrachtet wird die Strecke \([PQ]\) der Punkte \(P(x|f(x))\) und \(Q(x|g(x))\) mit derselben Abszisse.

b) Zeigen Sie, dass der Funktionsterm \(d(x) = -\sqrt{4 - x} -\sqrt{x + 2} + 6\) die Länge der Strecke \([PQ]\) in Abhängigkeit der \(x\)-Koordinate des Punktes \(P\) bzw. \(Q\) beschreibt, und geben Sie die Definitionsmenge der Funktion \(d\) an.

c) Bestimmen Sie die \(x\)-Koordinate des Punktes \(P\) bzw. \(Q\), für die die Länge der Strecke \([PQ]\) minimal ist.

Die Gerade \(x = -1\) und die Gerade \(x = 3\) schließen mit den Graphen \(G_{f}\) und \(G_{g}\) ein Flächenstück mit dem Flächeninhalt \(A\) ein.

d) Der Flächeninhalt \(A\) soll zunächst näherungsweise berechnet werden. Hierfür wird das Viereck \(SPQR\) betrachtet, welches die Punkte \(S(-1|f(-1))\), \(P(3|f(3))\), \(Q(3|g(3))\) und \(R(-1|g(-1))\) festlegen. Der Schnittpunkt der Strecken \([PR]\) und \([QS]\) halbiert die Strecken jeweils.

Zeichnen Sie das Viereck \(SPQR\) in die Abbildung ein und schraffieren Sie das Flächenstück mit dem Flächeninhalt \(A\). Beschreiben Sie die wesentlichen Schritte eines geeigneten Lösungsverfahrens, um \(A\) näherungsweise zu berechnen.

e) Berechnen Sie den exakten Wert des Flächeninhalts \(A\).

f) Betrachtet wird nun die Integralfunktion \(\displaystyle I \colon x \mapsto \int_{0}^{x} d(t) dt\).

Geben Sie an, welche der folgenden Terme die Maßzahl des Flächeninhalts \(A\) berechnen (Falsche Antworten zählen negativ).

Aufgabe 2

Zwei Seitenflächen eines Laplace-Würfels sind rot, drei sind gelb und eine Seitenfläche ist blau.

Wie viele Würfe sind mindestens nötig, um mit einer Wahrscheinlichkeit von mindestens 60 % mindestens dreimal die Farbe Rot zu erhalten.

Aufgabe 3

In einer Urne befinden sich eine gelbe und zwei blaue Kugeln. Es werden nacheinander drei Kugeln gezogen und deren Farbe notiert. Die gezogene Kugel wird jeweils zurückgelegt und zwei weitere Kugeln derselben Farbe in die Urne gegeben. Die Zufallsgröße \(X\) beschreibt die Anzahl der gezogenen gelben Kugeln.

a) Erstellen Sie ein vollständig beschriftetes Baumdiagramm und geben Sie den Ergebnisraum an.

b) Berechnen Sie die Wahrscheinlichkeit \(P(X \geq 1)\).

c) Beschreiben Sie im Sachzusammenhang ein Ereignis, dessen Wahrscheinlichkeit sich mithilfe des Terms \(1 - P(X = 3)\) berechnen lässt.

Aufgabe 4

Überprüfen Sie die Vektoren \(\overrightarrow{a} = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}\), \(\overrightarrow{b} = \begin{pmatrix} -2 \\ 3 \\ 4 \end{pmatrix}\) und \(\overrightarrow{c} = \begin{pmatrix} 3 \\ -3 \\ 1 \end{pmatrix}\) auf lineare Abhängigkeit und deuten Sie das Ergebnis geometrisch.

Aufgabe 5

Die Punkte \(A(0|2|2)\), \(B(2|3|0)\) und \(C(0|-2|4)\) legen die Ebene \(E\) fest.

a) Ermitteln Sie eine Gleichung der Ebene \(E\) in Normalenform.

(mögliches Ergebnis: \(E \colon 3x_{1} + 2x_{2} + 4x_{3} = 12\))

b) Ermitteln Sie die Koordinaten der Schnittpunkte \(S_{1}\), \(S_{2}\) und \(S_{3}\) der Ebene \(E\) mit der \(x_{1}\)-, \(x_{2}\)- bzw. \(x_{3}\)-Achse und veranschaulichen Sie die Lage der Ebene \(E\) in einem kartesischen Koordinatensystem.

c) Bestimmen Sie eine Gleichung der Schnittgeraden \(s\) der Ebene \(E\) und der \(x_{2}x_{3}\)-Ebene.

d) Berechnen Sie die Koordinaten des Punktes \(S'\), der durch Spiegelung des Punktes \(S_{1}\) an der Geraden \(s\) hervorgeht.