Geben sie jeweils eine Integrandenfunktion \(f(x)\) und \(g(x)\) an, sodass die folgenden Gleichungen erfüllt sind.

Anmerkung:

Die Integrandenfunktionen \(f(x)\) und \(g(x)\) sind lediglich anzugeben. Jede Erklärung oder Rechnung kann entfallen.

a) \(\displaystyle \int_{-a}^{+a} f(x) dx = 0; \; a \neq 0\)

Beispielsweise: \(f(x) = x\), \(f(x) = x^{3}\) oder \(f(x) = \sin{x}\)

Begründung:

Der Wert des bestimmten Integrals \(\displaystyle \int_{-a}^{+a} f(x) dx; \; a \neq 0\) ist gleich der Maßzahl des Flächeninhalts des Flächenstücks, das der Graph der Integrandenfunktion \(f(x)\) für \(x \in [-a;+a]\) mit der \(x\)-Achse einschließt. Dabei zählen die Flächeninhalte der Flächenstücke unterhalb der \(x\)-Achse negativ und die Flächeninhalte der Flächenstücke oberhalb der \(x\)-Achse positiv.

Die Gleichung \(\displaystyle \int_{-a}^{+a} f(x) dx = 0; \; a \neq 0\) besagt demnach, dass die Flächenbilanz der für \(x \in [-a;+a]\) betrachteten Flächenstücke gleich Null ist.

Dies triff insbesondere auf Graphen von zum Koodinatenursprung punktsymmetrischen Integrandenfunktionen zu, wie beispielsweise

• eine lineare Funktion der Form \(f(x) = mx; \; m \neq 0\) oder
• eine Potenzfunktion \(f(x) = ax^{n}; \; a \neq 0\) mit ungeradem Exponenten \(n \in \mathbb N\) oder
• eine Sinusfunktion der Form \(f(x) = a \cdot \sin{(bx)}; \; a, b \neq 0\).

Im einfachsten Fall wählt man

\(f(x) = x\) oder

\(f(x) = x^{3}\) oder

\(f(x) = \sin{x}\).

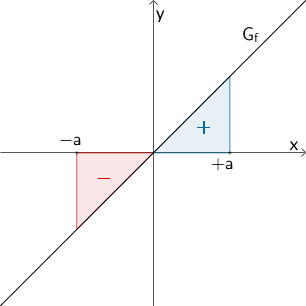
Veranschaulichung als Flächenbilanz: Der Wert des Integrals \(\displaystyle \int_{-a}^{+a} f(x) dx\) mit der zum Koordinatenursprung punktsymmetrischen Integrandenfunktion \(f \colon x \mapsto x\) ist gleich Null.

Nachweis:

\[\begin{align*} \int_{-a}^{+a} x dx &= \left[ \frac{1}{2}x^{2} \right]_{-a}^{+a} \\[0.8em] &= \frac{1}{2} \cdot (+a)^{2} - \frac{1}{2} \cdot (-a)^{2} \\[0.8em] &= \frac{1}{2}a^{2} - \frac{1}{2}a^{2} \\[0.8em] &= 0 \end{align*}\]

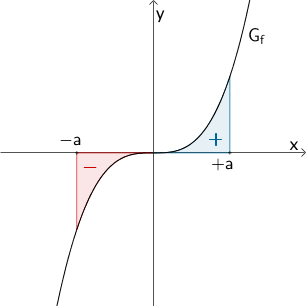
Veranschaulichung als Flächenbilanz: Der Wert des Integrals \(\displaystyle \int_{-a}^{+a} f(x) dx\) mit der zum Koordinatenursprung punktsymmetrischen Integrandenfunktion \(f \colon x \mapsto x^{3}\) ist gleich Null.

Nachweis:

\[\begin{align*} \int_{-a}^{+a} x^{3} dx &= \left[ \frac{1}{4}x^{4} \right]_{-a}^{+a} \\[0.8em] &= \frac{1}{4} \cdot (+a)^{4} - \frac{1}{4} \cdot (-a)^{4} \\[0.8em] &= \frac{1}{4}a^{4} - \frac{1}{4}a^{4} \\[0.8em] &= 0 \end{align*}\]

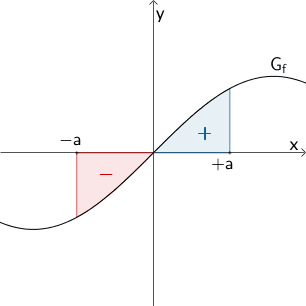
Veranschaulichung als Flächenbilanz: Der Wert des Integrals \(\displaystyle \int_{-a}^{+a} f(x) dx\) mit der zum Koordinatenursprung punktsymmetrischen Integrandenfunktion \(f \colon x \mapsto \sin{x}\) ist gleich Null.

Nachweis:

\[\begin{align*} \int_{-a}^{+a} \sin{x} dx &= \left[ \cos{x} \right]_{-a}^{+a} \\[0.8em] &= \cos{(+a)} - \cos{(-a)} & &| \; \cos{(-x)} = \cos{x} \\[0.8em] &= \cos{a} - \cos{a} \\[0.8em] &= 0 \end{align*}\]

b) \(\displaystyle \int_{-1}^{3} g(x) dx = 8\)

Beispielsweise: \(g(x) = 2\)

Begründung:

Es gibt unendliche viele mögliche Funktionen \(g(x)\), welche die Gleichung \(\displaystyle \int_{1}^{3} g(x) dx = 8\) erfüllen.

Graphisch interpretiert sagt die Gleichung aus, dass das Flächenstück, welches der Graph der gesuchten Integrandenfunktion \(g(x)\) für \(x \in [-1;3]\) mit der \(x\)-Achse einschließt, einen Flächeninhalt von 8 FE (Flächeneinheiten) hat.

Beschränkt man sich bei dieser graphischen Betrachtung auf ein Rechteck, kommt für \(g(x)\) nur eine konstante Funktion in Frage. Die Länge des Rechtecks ist mit 4 LE (Längeneinheiten) durch die Integrationsgrenzen \(-1\) und \(3\) vorgegeben. Folglich muss die konstante Funktion \(g(x) = 2\) lauten.

Veranschaulichung der Gleichung \(\displaystyle \int_{-1}^{3} g(x) dx = 8\) mit \(g(x) = 2\): Der Graph \(G_{g}\) der Integrandenfunktion \(g\) schließt für \(x \in [-1;3]\) mit der \(x\)-Achse ein Flächenstück mit dem Flächeninhalt 8 FE ein

Nachweis:

\[\begin{align*}\int_{-1}^{3} 2 dx &= [2x]_{-1}^{3} \\[0.8em] &= 2 \cdot 3 -  2 \cdot (-1) \\[0.8em] &= 6 + 2 \\[0.8em] &= 8 \end{align*}\]