Berechnen Sie die Zunahme der Staulänge von 06:30 Uhr bis 08:00 Uhr und bestimmen Sie für diesen Zeitraum die mittlere Änderungsrate der Staulänge.
(3 BE)
Lösung zu Teilaufgabe 1f
\[s(x) = \left( \frac{x}{4} \right)^2 \cdot (4 - x)^3 = -\frac{1}{16}x^5 + \frac{3}{4}x^4 - 3x^3 + 4x^2; \; D_s = \mathbb R\]
Zunahme der Staulänge von 06:30 Uhr bis 08:00 Uhr
06:30 Uhr entspricht \(x = 0{,}5\), 08:00 Uhr entspricht \(x = 2\) (vgl. Angabe Aufgabe 1)
Die Differenz \(s(2) - s(0{,}5)\) errechnet die Zunahme der Staulänge von 06:30 Uhr bis 08:00 Uhr.
\[\begin{align*} s(\textcolor{#e9b509}{2}) - s(\textcolor{#0087c1}{0{,}5}) &= \left( \frac{\textcolor{#e9b509}{2}}{4} \right)^2 \cdot (4 - \textcolor{#e9b509}{2})^3 - \left( \frac{\textcolor{#0087c1}{0{,}5}}{4} \right)^2 \cdot (4 - \textcolor{#0087c1}{0{,}5})^3 \\[0.8em] &= 2 - \frac{343}{512} = \frac{681}{512} \approx 1{,}33\end{align*}\]
Die Staulänge nimmt von 06:30 Uhr bis 08:00 Uhr um etwa 1,33 km zu.
Mittlere Änderungsrate der Staulänge für den Zeitraum 06:30 Uhr bis 08:00 Uhr
Differenzenquotient oder mittlere Änderungsrate
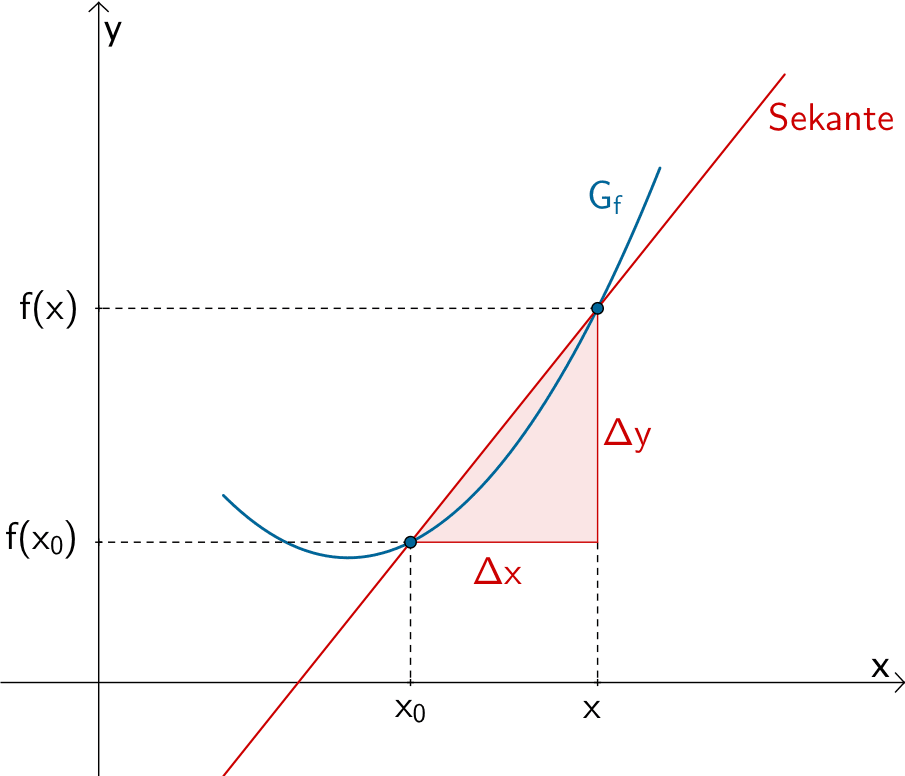
Der Differenzenquotient oder die mittlere Änderungsrate \(m_{s} = \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt die Steigung der Sekante durch den Punkt \((x_{0}|f(x_{0}))\) und einen weiteren Punkt des Graphen der Funktion \(f\).
MIt \(s(2) - s(0{,}5) \approx 1{,}33\;\text{km}\) ergibt sich:
\[m_s = \frac{s(2) - s(0{,}5)}{2 - 0{,}5} = \frac{1{,}33\;\text{km}}{1{,}5\;\text{h}} \approx 0{,}89\;\frac{\text{km}}{\text{h}}\]


