Weisen Sie nach, dass für \(0 \leq x \leq 5\) die Gleichung \(f(5 - x) = f(5 + x)\) erfüllt ist, indem Sie die Terme \(f(5 - x)\) und \(f(5 + x)\) geeignet umformen. Begründen Sie damit, dass der Graph \(G_f\) symmetrisch bezüglich der Gerade mit der Gleichung \(x = 5\) ist.
(5 BE)
Lösung zu Teilaufgabe d
Nachweis, dass für \(0 \leq x \leq 5\) die Gleichung \(f(5 - x) = f(5 + x)\) erfüllt ist
\[f(x) = 2 \cdot \sqrt{10x - x^2}\]
\[\begin{align*}f(\textcolor{#0087c1}{5 - x}) &= 2 \cdot \sqrt{10 \cdot \textcolor{#0087c1}{(5 - x)} - \textcolor{#0087c1}{(5 - x)}^2} &&| \; \text{2. Binomische Formel anwenden} \\[0.8em] &= 2 \cdot \sqrt{50 - 10x - (25 - 10x + x^2)} \\[0.8em] &= 2 \cdot \sqrt{50 - 10x - 25 + 10x - x^2} \\[0.8em] &= 2 \cdot \sqrt{-x^2 + 25}\end{align*}\]
\[\begin{align*}f(\textcolor{#0087c1}{5 + x}) &= 2 \cdot \sqrt{10 \cdot \textcolor{#0087c1}{(5 + x)} - \textcolor{#0087c1}{(5 + x)}^2} &&| \; \text{1. Binomische Formel anwenden} \\[0.8em] &= 2 \cdot \sqrt{50 + 10x - (25 + 10x + x^2)} \\[0.8em] &= 2 \cdot \sqrt{50 + 10x - 25 - 10x - x^2} \\[0.8em] &= 2 \cdot \sqrt{-x^2 + 25}\end{align*}\]
Somit ist die Gleichung \(f(5 - x) = f(5 + x)\) für \(0 \leq x \leq 5\) erfüllt.
Begründung, dass der Graph \(G_f\) symmetrisch bezüglich der Gerade mit der Gleichung \(x = 5\) ist
\[f(\textcolor{#0087c1}{5 - x}) = f(\textcolor{#0087c1}{5 + x}) = 2 \cdot \sqrt{-x^2 + 25}; \; 0 \leq x \leq 5\]
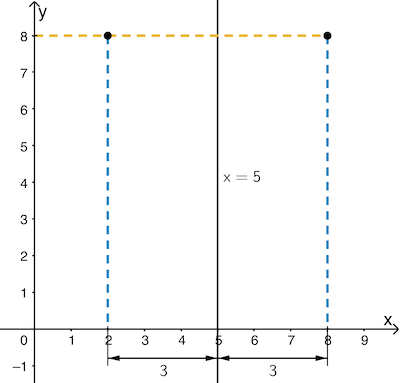
Die Gleichung sagt aus, dass der Funktionswert von zwei \(\textcolor{#0087c1}{x}\)-Werten, die von 5 den gleichen Abstand haben, stets der gleiche ist. Deshalb liegen die zugehörigen Graphenpunkte symmetrisch bezüglich der Gerade mit der Gleichung \(x = 5\).
Beispiel (nicht verlangt):
Die \(\textcolor{#0087c1}{x}\)-Werte \(\textcolor{#0087c1}{5 - 3 = 2}\) und \(\textcolor{#0087c1}{5 + 3 = 8}\) haben von 5 den gleichen Anstand 3. Ihnen wird der gleiche Funktionswert \(\textcolor{#e9b509}{2 \cdot \sqrt{-3^2 + 25} = 8}\) zugeordnet.