Der Graph der Funktion \(g^{*}\) geht aus \(G_{g}\) durch Strecken und Verschieben hervor. Die Wertemenge von \(g^{*}\) ist \(]-1;1[\). Geben Sie einen möglichen Funktionsterm für \(g^{*}\) an.

(2 BE)

Lösung zu Teilaufgabe 2c

Zum Beispiel:

\(g^{*}(x) = 2 \cdot g(x) -1\)

oder

\(g^{*}(x) = 2 \cdot \dfrac{e^{x}}{e^{x} + 1} - 1\)

Begründung (nicht verlangt)

\[g^{*}(x) = \textcolor{#e9b509}{2} \cdot g(x) \textcolor{#0087c1}{- 1}\]

Der Graph der Funktion \(g^{*}\) geht aus dem Graphen der Funktion \(g\) wie folgt hervor:

1. Schritt

Streckung in y-Richtung mit dem Faktor 2 

Die Streckung verändert die Wertemenge von \(]0;1[\) zu \(\textcolor{#e9b509}{]0;2[}\).

2. Schritt

Verschiebung in y-Richtung um -1 LE (Längeneinheiten)

Die Verschiebung verändert die Wertemenge von \(\textcolor{#e9b509}{]0;2[}\) zu \(\textcolor{#0087c1}{]-1;1[}\).

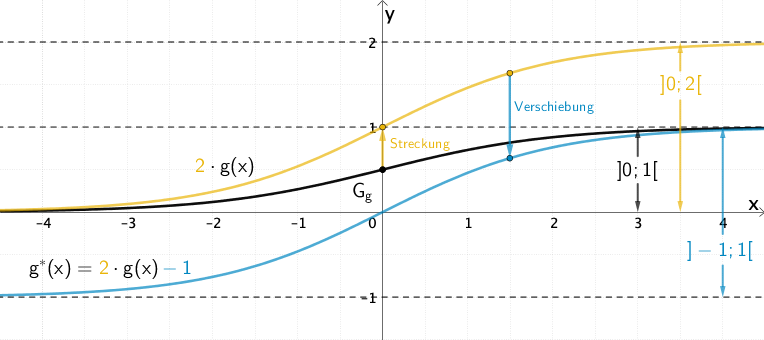
Entstehung des Graphen der Funktion \(g^{*}\) aus dem Graphen der Funktion \(g\)