Jeder Körper sendet elektromagnetische Strahlung unterschiedlicher Frequenzen aus; die Intensität der Strahlung hängt von der Frequenz der Strahlung ab. Im Idealfall lässt sich diese Intensität nach Max Planck durch die Schar der in \(\mathbb R^+\) definierten Funktionen
\[I_T\,\colon x \mapsto \frac{x^3}{e^{\frac{x}{T}} - 1}\]
mit \(T \in \mathbb R^+\) beschreiben. Dabei ist \(x\) - bis auf eine Konstante - die Frequenz der Strahlung und \(T\) die Temperatur des Körpers in Kelvin.
Die Abbildung zeigt die zu drei Werten des Parameters \(T\) gehörenden Graphen von \(I_T\).
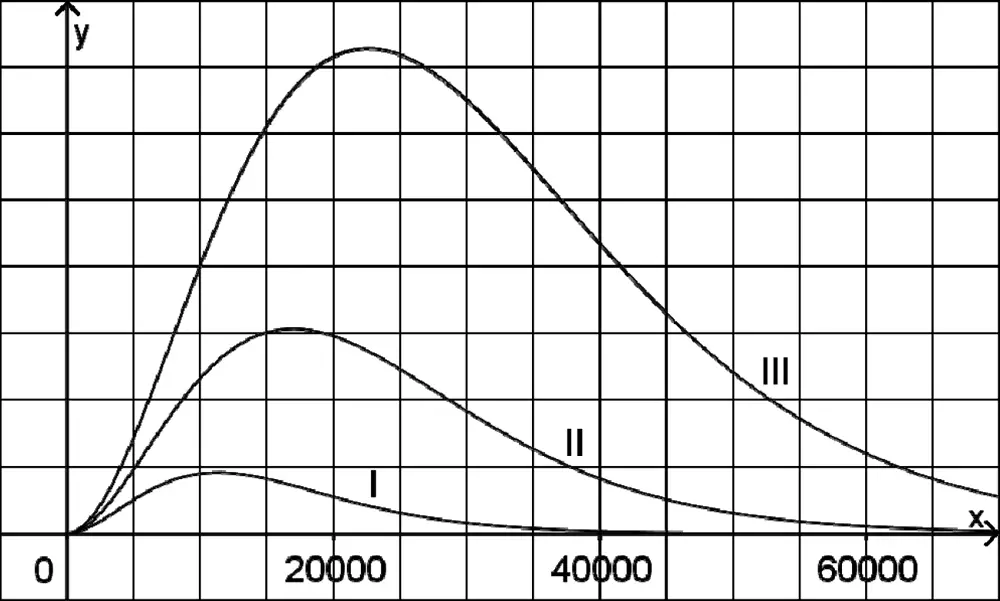
Bei der Bearbeitung der folgenden Aufgaben soll auf die Verwendung von Einheiten verzichtet werden.
Weisen Sie anhand des Funktionsterms von \(I_T\) nach, dass der Wert der Intensität der Strahlung stets positiv ist.
(3 BE)
Lösung zu Teilaufgabe 2a
\[I_{T}(x) = \frac{x^3}{e^{\frac{x}{T}} - 1}\,; \quad D = \mathbb R^{+}, \, T \in \mathbb R^{+}\]
Betrachtung des Zählerterms:
\(x^3 > 0\) für \(x \in \mathbb R^+\)
Betrachtung des Nennerterms:
\(\frac{x}{T} > 0\) für \(x \in \mathbb R^{+},\, T \in \mathbb R^{+}\)
\(\Longrightarrow \quad e^{\frac{x}{T}} > 1\) für \(\frac{x}{T} > 0\)
\(\Longrightarrow \quad e^{\frac{x}{T}} - 1 > 0\) für \(e^{\frac{x}{T}} > 1\)
\(\Longrightarrow \quad I_{T}(x) > 0\) für \(x \in \mathbb R^{+}, \, T \in \mathbb R^{+}\)
Der Wert der Intensität der Strahlung ist stets positiv.


