- Details
- Kategorie: Analysis I - Teil 1
Gegeben ist die Funktion \(g \colon x \mapsto \sqrt{3x + 9}\) mit maximaler Definitionsmenge \(D\).
Bestimmen Sie \(D\) und geben Sie die Nullstelle von \(g\) an.
(3 BE)
- Details
- Kategorie: Analysis I - Teil 1
Ermitteln Sie die Gleichung der Tangente an den Graphen von \(g\) im Punkt \(P\,(0|3)\).
(4 BE)
- Details
- Kategorie: Analysis I - Teil 1
Geben Sie jeweils den Term einer in \(\mathbb R\) definierten Funktion an, die die angegebene Wertemenge \(\mathbb W\) hat.
\(\mathbb W = [2; + \infty[\)
(2 BE)
- Details
- Kategorie: Analysis I - Teil 1
Geben Sie jeweils den Term einer in \(\mathbb R\) definierten Funktion an, die die angegebene Wertemenge \(\mathbb W\) hat.
\(\mathbb W = [-2;2]\)
(2 BE)
- Details
- Kategorie: Analysis I - Teil 1
Geben Sie für \(x \in \mathbb R^+\) die Lösungen der folgenden Gleichung an:
\[(\ln x - 1) \cdot (e^x - 2) \cdot \left( \frac{1}{x} - 3 \right) = 0\]
(3 BE)
- Details
- Kategorie: Analysis I - Teil 1
Abbildung 1 zeigt den Graphen \(G_f\) einer in \(\mathbb R\) definierten Funktion \(f\).
Skizzieren Sie in Abbildung 1 den Graphen der in \(\mathbb R\) definierten Integralfunktion \(\displaystyle F \colon x \mapsto \int_1^x f(t)\,dt\). Berücksichtigen Sie dabei mit jeweils angemessener Genauigkeit insbesondere die Nullstellen und Extremstellen von \(F\) sowie \(F(0)\).
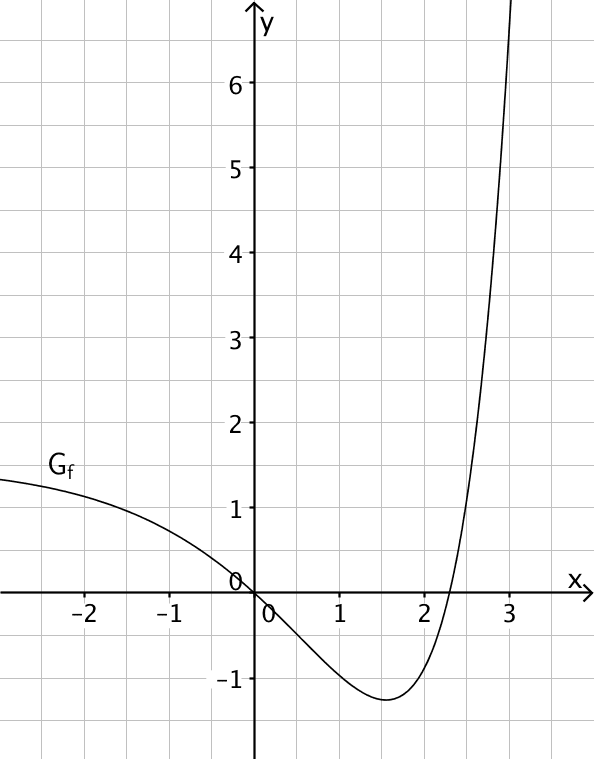Abb. 1
(6 BE)
