Deuten Sie die Aussage \(F(2{,}5) - F(0) \approx 0\) in Bezug auf \(G_{f}\) geometrisch.
(2 BE)
Lösung zu Teilaufgabe 1f
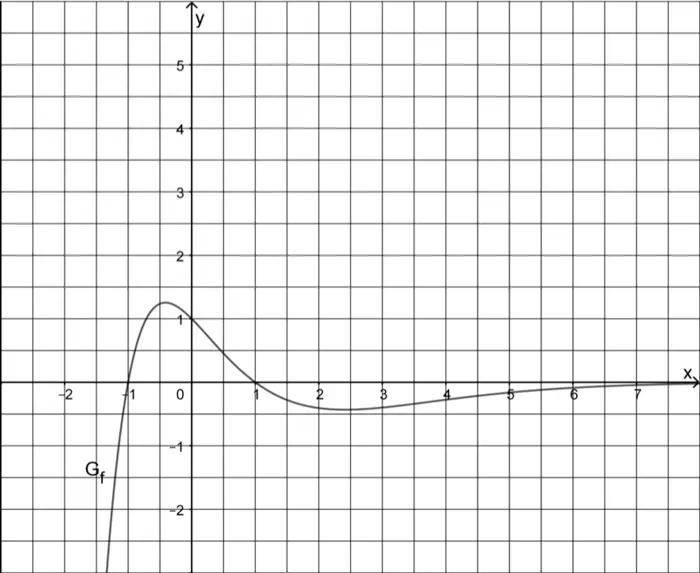
Die Aussage \(F(2{,}5) - F(0) \approx 0\) bedeutet, dass die Inhalte der beiden Flächen, die \(G_{f}\) im Intervall \([0;2{,}5]\) mit der \(x\)-Achse einschließt, etwa gleich groß sind.
Begründung (nicht verlangt)
![Flächen, die der Graph der Funktion f im Intervall [0;2,5] mit der x-Achse einschließt](/images/stories/B2021_PT_B_A2/B2021_PT_B_A2_1f.png)
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[F(2{,}5) - F(0) = \int_{0}^{2{,}5}f(x)dx \approx 0\]
Der Wert des bestimmten Integrals \(\displaystyle \int_{0}^{2{,}5}f(x)dx\) entspricht der Flächenbilanz der Inhalte der Flächen, die \(G_{f}\) im Intervall \([0;2{,}5]\) mit der \(x\)-Achse einschließt.
Dabei trägt der Inhalt der im Intervall \([0;1]\) oberhalb der \(x\)-Achse liegenden Fläche positiv und der Inhalt der im Intervall \([1;2{,}5]\) unterhalb der \(x\)-Achse liegenden Fläche negativ zur Flächenbilanz bei.
Aus \(\displaystyle F(2{,}5) - F(0) = \int_{0}^{2{,}5}f(x)dx \approx 0\) folgt, dass die Flächenbilanz näherungsweise gleich null ist. Somit sind die Inhalte der beiden Flächen etwa gleich groß.


