Bestimmen Sie, wie groß \(n\) mindestens sein muss, damit die Wahrscheinlichkeit dafür, dass sich drei verschiedene Motive auf den Ansteckern befinden, größer als 90 % ist.
(3 BE)
Lösung zu Teilaufgabe 4c
Der Term, mit dem sich die Wahrscheinlichkeit dafür bestimmen lässt, dass sich drei verschiedene Motive auf den Anstecken befinden, ist aus Teilaufgabe 4b bekannt.
\[P(\text{„Drei verschiedene Motive"}) = \frac{(n - 1) \cdot (n - 2)}{n^{2}}\]
Diese Wahrscheinlichkeit soll größer als 90 % sein. Nach geeigneten Umformungen ergibt die Bedingung eine quadratische Ungleichung.
\[\begin{align*}\frac{(n - 1) \cdot (n - 2)}{n^{2}} &> 0{,}9 &&| \cdot n^{2} \\[0.8em] (n - 1)(n - 2) &> 0{,}9n^{2} \\[0.8em] n^{2} - n - 2n + 2 &> 0{,}9n^{2} &&| - 0{,}9n^{2} \\[0.8em] 0{,}1n^{2} - 3n + 2 &> 0 &&| \; n > 0; \; n \in \mathbb N \end{align*}\]
Die rechnerische Lösung einer quadratischen Ungleichung ist relativ aufwendig, weshalb eine anschauliche halbgraphische Lösung vorzuziehen ist (vgl. Abiturskript - 1.1.2 Quadratische Funktion, Quadratische Ungleichungen).
Zunächst werden die Nullstellen der quadratischen Gleichung \(\textcolor{#cc071e}{0{,}1}n^{2} \textcolor{#0087c1}{- 3}n + \textcolor{#e9b509}{2} = 0\) mithilfe der Lösungsformel für quadratische Gleichungen (Mitternachtsformel) bestimmt.
Anschließend wird die nach oben geöffnete Parabel (positiver Öffnungsfaktor) des quadratischen Terms \(\textcolor{#cc071e}{0{,}1}n^{2} - 3n + 2\) qualitativ skizziert.
Anhand der Nullstellen lässt sich nun der Bereich formulieren, in dem die Parabel im Positiven verläuft, also \(0{,}1n^{2} - 3n + 2 \textcolor{#89ba17}{>} 0\) gilt.
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*}n_{1,2} &= \frac{-\textcolor{#0087c1}{(-3)} \pm \sqrt{\textcolor{#0087c1}{(-3)}^{2} - 4 \cdot \textcolor{#cc071e}{0{,}1} \cdot \textcolor{#e9b509}{2}}}{2 \cdot \textcolor{#cc071e}{0{,}1}} \\[0.8em] &= \frac{3 \pm \sqrt{8{,}2}}{0{,}2} \\[0.8em] \Rightarrow \enspace n_{1} &= \frac{3 - \sqrt{8{,}2}}{0{,}2} = 0{,}68\dots \\[0.8em] n_{2} &= \frac{3 + \sqrt{8{,}2}}{0{,}2} = 29{,}31\dots\end{align*}\]
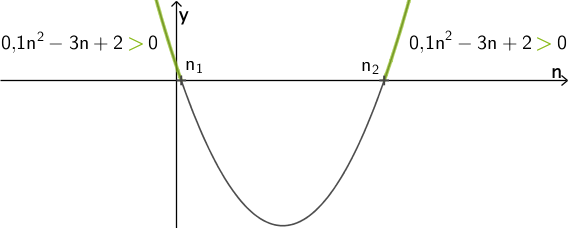
Für \(n \textcolor{#89ba17}{<} n_{1}\) und \(n \textcolor{#89ba17}{>} n_{2}\) verläuft die Parabel im Positiven, das heißt, für \(n \textcolor{#89ba17}{<} n_{1}\) und \(n \textcolor{#89ba17}{>} n_{2}\) ist die Ungleichung \(0{,}1n^{2} - 3n + 2 \textcolor{#89ba17}{>} 0\) erfüllt.
Allerdings kommt \(n < n_{1}\) im Sachzusammenhang nicht in Betracht, da die Anzahl verschiedener Motive größer als eins sein muss.
Somit folgt:
\[\begin{align*}n &\textcolor{#89ba17}{>} n_{2} \\[0.8em]n &\textcolor{#89ba17}{>} 29{,}31\dots &&| \; n \in \mathbb N\;\text{(Anzahl ist ganzzahlig)}\\[0.8em]\Rightarrow \enspace n &= 30\end{align*}\]
Damit die Wahrscheinlichkeit dafür, dass sich drei verschiedene Motive auf den Ansteckern befinden, größer als 90 % ist, muss die Anzahl \(n\) der verschiedenen Motive mindestens 30 sein.
Anmerkung:
Bei dieser Aufgabe handelt es sich nicht um eine klassische „3-Mindestens-Aufgabe", die nach der Länge \(n\) einer Bernoulli-Kette fragt wie beispielsweise Teilaufgabe 2c Stochastik 1 Prüfungsteil B Mathematik Abitur Bayern 2020.


