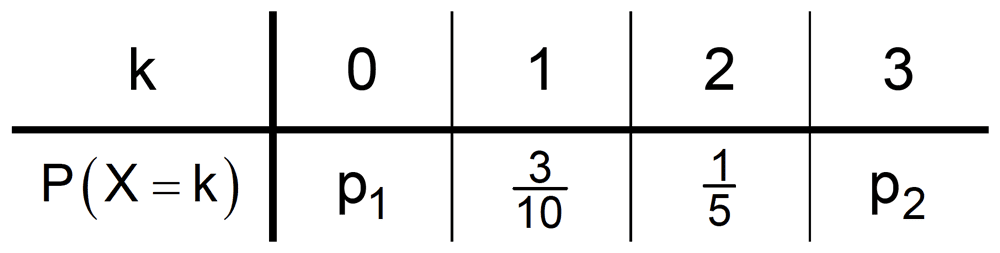Die Zufallsgröße \(X\) kann die Werte 0, 1, 2 und 3 annehmen. Die Tabelle zeigt die Wahrscheinlichkeitsverteilung von \(X\) mit \(p_1, p_2 \in [0;1]\).
Zeigen Sie, dass der Erwartungswert von \(X\) nicht größer als 2,2 sein kann.
(3 BE)
Lösung zu Teilaufgabe 3
Die Größe des Erwartungswerts der Zufallsgröße \(X\) ist von den beiden unbekannten Wahrscheinlichkeiten \(p_1\) und \(p_2\) abhängig. Um die möglichen Werte der Wahrscheinlichkeiten festlegen zu können, müssen zwei Bedingungen mit \(p_1\) und \(p_2\) formuliert werden.
Erwartungswert der Zufallsgröße \(X\) in Abhängigkeit von \(p_1\) und \(p_2\) bestimmen (erste Bedingung):
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(\boldsymbol{X}\)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot P(X = x_i) \\[0.8em] &= x_{1} \cdot P(X = x_1) + x_{2} \cdot P(X = x_2) + \cdots + x_{n} \cdot P(X = x_n) \end{align*}\]
Der Erwartungswert \(\mu = E(X)\) gibt den Mittelwert einer Zufallsgröße \(X\) pro Versuch an, der bei sehr häufiger Durchführung eines Zufallsexperiments (auf lange Sicht) zu erwarten ist.
\[\begin{align*} E(X) &= 0 \cdot p_1 + 1 \cdot \frac{3}{10} + 2 \cdot \frac{1}{5} + 3 \cdot p_2 \\[0.8em] &= \frac{3}{10} + \frac{2}{5} + 3p_2 \\[0.8em] &= \frac{3}{10} + \frac{4}{10} + 3p_2 \\[0.8em] &= \frac{7}{10} + 3p_2 \end{align*}\]
Die Summe der Wahrscheinlichkeiten \(P(X = k)\) ist gleich Eins (zweite Bedingung).
\[\begin{align*} \sum P(X = k) &= 1 \\[0.8em] p_1 + \frac{3}{10} + \frac{1}{5} + p_2 &= 1 \\[0.8em] p_1 + \frac{3}{10} + \frac{2}{10} + p_2 &= 1 \\[0.8em] p_1 + \frac{1}{2} + p_2 &= 1 & &| -\frac{1}{2} \\[0.8em] p_1 + p_2 = \frac{1}{2}\end{align*}\]
Wahrscheinlichkeiten \(p_1\) und \(p_2\) für den größtmöglichen Erwartungswert der Zufallsgröße \(X\) festlegen:
Der Erwartungswert \(\displaystyle E(X) = \frac{7}{10} + 3p_2\) ist am größten, wenn die Wahrscheinlichkeit \(p_2\) den größtmöglichen Wert annimmt.
\[\left. \begin{align*} E(X) &= \frac{7}{10} + 3p_2 \\ p_1 + p_2 &= \frac{1}{2} \end{align*} \right\} \enspace \Rightarrow \enspace p_1 = 0\,; \enspace p_2 = \frac{1}{2}\]
Größtmöglichen Erwartungswert der Zufallsgröße \(X\) berechnen:
\[\begin{align*}E(X) &= \frac{7}{10} + 3 \cdot \frac{1}{2} \\[0.8em] &= \frac{7}{10} + \frac{3}{2} \\[0.8em] &= \frac{7}{10} + \frac{15}{10} \\[0.8em] &= \frac{22}{10} = 2{,}2 \end{align*}\]
\(\Longrightarrow \quad\) Der Erwartungswert der Zufallsgröße \(X\) kann nicht größer als 2,2 sein.
