Lagebeziehung zweier Kugeln
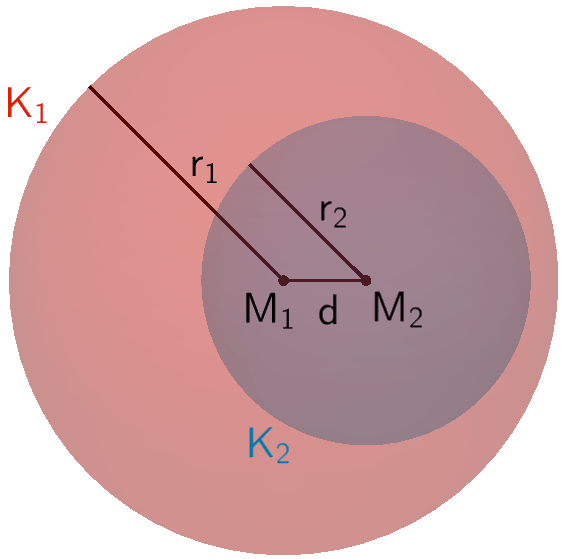
Die gegenseitige Lage zweier Kugeln \(K_{1}\) und \(K_{2}\) wird durch den Abstand \(d(M_{1};M_{2})\) ihrer Mittelpunkte \(M_{1}\) und \(M_{2}\) bestimmt.
Es lassen sich fünf Fälle unterscheiden:
Die Kugeln \(K_{1}\) und \(K_{2}\) haben keine gemeinsamen Punkte.
\[d(M_{1};M_{2}) > r_{1} + r_{2}\]
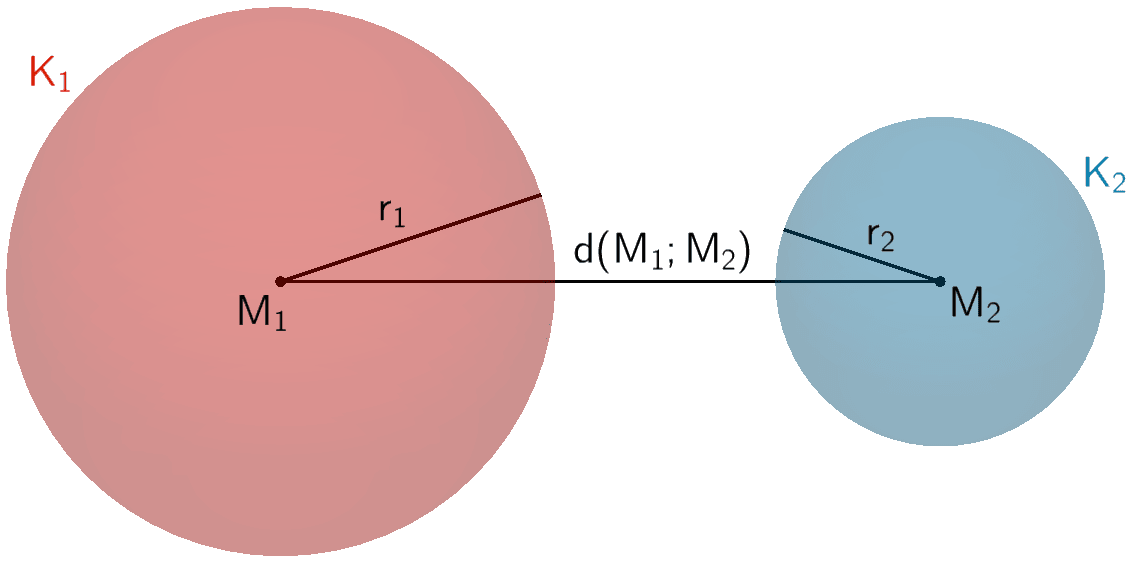
Die Kugeln \(K_{1}\) und \(K_{2}\) berühren sich von außen in einem Punkt.
\[d(M_{1};M_{2}) = r_{1} + r_{2}\]
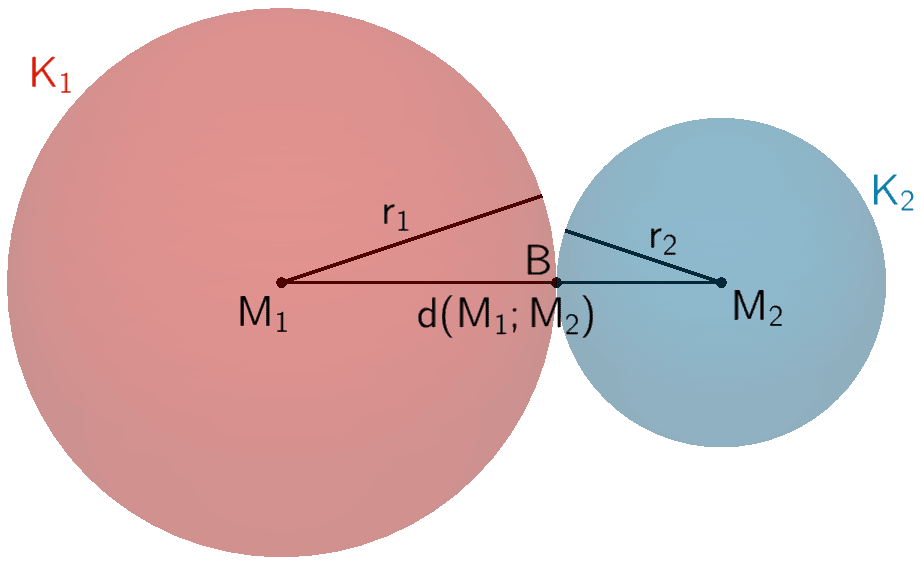
Die Kugeln \(K_{1}\) und \(K_{2}\) schneiden sich in einem Schnittkreis.
\[\vert r_{1} - r_{2} \vert < d(M_{1};M_{2}) < r_{1} + r_{2}\]
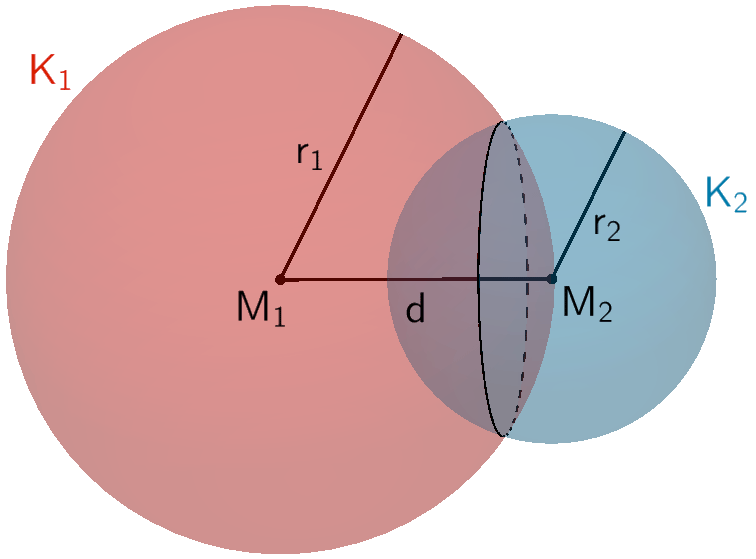
Die Kugeln \(K_{1}\) und \(K_{2}\) berühren sich von innen in einem Punkt.
\[d(M_{1};M_{2}) = \vert r_{1} - r_{2} \vert\]
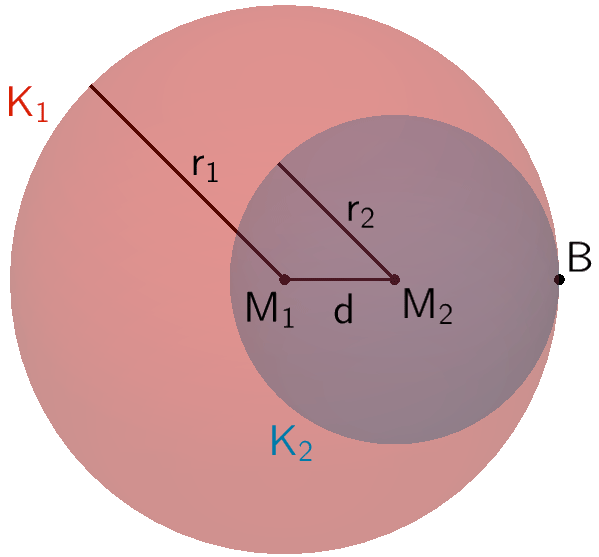
Die Kugeln \(K_{1}\) und \(K_{2}\) liegen ineinander.
\[d(M_{1};M_{2}) < \vert r_{1} - r_{2} \vert\]
Beispielaufgabe
Gegeben seien die Kugeln
\(K_{1} \colon (x_{1} - 1)^{2} + (x_{2} - 2)^{2} + (x_{3} - 3)^{2} = 49\) und
\(K_{2} \colon (x_{1} + 6)^{2} + (x_{2} + 5)^{2} + (x_{3} + 4)^{2} =36\).
Untersuchen Sie die gegenseitigen Lage der Kugeln \(K_{1}\) und \(K_{2}\).
\[K_{1} \colon (x_{1} - 1)^{2} + (x_{2} - 2)^{2} + (x_{3} - 3)^{2} = 49\]
\[\Longrightarrow \quad M_{1}(1|2|3), \, r_{1} = 7\]
\[K_{2} \colon (x_{1} + 6)^{2} + (x_{2} + 5)^{2} + (x_{3} + 4)^{2} =36\]
\[\Longrightarrow \quad M_{2}(-6|-5|-4), \, r_{2} = 6\]
Abszand \(d(M_{1};M{2})\) der Kugelmittelpunkte berechnen:
\[\begin{align*} d(M_{1};M_{2}) &= \vert \overrightarrow{M_{1}M_{2}} \vert \\[0.8em] &= \vert \overrightarrow{M}_{2} - \overrightarrow{M}_{1} \vert \\[0.8em] &= \left| \begin{pmatrix} -6 \\ -5 \\ -4 \end{pmatrix} - \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} -7 \\ -7 \\ -7 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-7)^{2} + (-7)^{2} + (-7)^{2}} \\[0.8em] &= \sqrt{147} \\[0.8em] &= 7\sqrt{3} \\[0.8em] &\approx 12{,}1 \end{align*}\]
Summe und positive Differenz der Kugelradien berechnen:
\[r_{1} + r_{2} = 7 + 6 = 13\]
\[\vert r_{1} - r_{2} \vert = 7 - 6 = 1\]
Schlussfolgerung:
\[\Longrightarrow \quad \vert r_{1} - r_{2} \vert < d(M_{1};M_{2}) < r_{1} + r_{2}\]
\(\Longrightarrow \quad\)Die Kugeln \(K_{1}\) und \(K_{2}\) schneiden sich in einem Schnittkreis.

