Der Graph von \(f\) schließt mit den Koordinatenachsen ein Flächenstück ein, das durch das Dreieck mit den Eckpunkten \(O(0|0)\), \(P(\ln 2|0)\) und \(Q(0|2)\) angenähert werden kann. Berechnen Sie, um wie viel Prozent der Flächeninhalt des Dreiecks \(OPQ\) vom Inhalt des Flächenstücks abweicht.
(4 BE)
Lösung zu Teilaufgabe 1f
Bestimmtes Integral berechnen, prozentuale Abweichung zweier Flächeninhalte
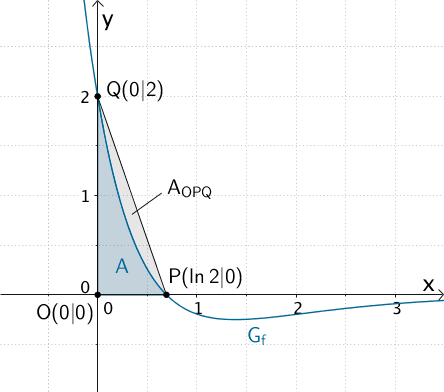
Flächenstück mit dem Flächeninhalt \(A\), das der Graph der Funktion \(f\) mit den Koordinatenachsen einschließt und rechtwinkliges Dreieck \(OPQ\) mit dem Flächeninhalt \(A_{OPQ}\)
Flächeninhalt \(A_{OPQ}\) des Dreieck \(OPQ\)
\[\begin{align*} A_{OPQ} &= \frac{1}{2} \cdot \overline{OP} \cdot \overline{OQ} \\[0.8em] &= \frac{1}{2} \cdot \ln{2} \cdot 2 \\[0.8em] &= \ln{2} \end{align*}\]
Flächeninhalt \(A\) des Flächenstücks, das \(G_{f}\) mit den Koordinatenachsen einschließt
Der Wert des bestimmten Integrals \(\displaystyle \int_{0}^{\ln{2}} f(x) dx\) ist gleich der Maßzahl des Flächeninhalts \(A\) des Flächenstücks, das der Graph der Funktion \(f\) mit den Koordinatenachsen einschließt.
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\(\displaystyle A = \int_{0}^{\ln{2}} f(x) dx\) mit \(f(x) = 2e^{-x} \cdot \left( 2e^{-x} - 1\right); \; D_{f} = \mathbb R\) (vgl. Angabe Aufgabe 1)
1. Möglichkeit: Angabe zu Teilaufgabe 1d sowie Ergebnis aus Teilaufgabe 1e berücksichtigen
In der Angabe zu Teilaufgabe 1d heißt es: „Der Graph von \(F\) verläuft durch den Punkt \((\ln{2}|0{,}5)\)."
\[\Longrightarrow \quad F(\ln{2}) = 0{,}5\]
Aus Teilaufgabe 1e ist bekannt:
\[F(0) = 0\]
Damit lässt sich der Flächeninhalt \(A\) berechnen:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[A = \int_{0}^{\ln{2}} f(x) dx = F(\ln{2}) - F(0) = 0{,}5 - 0 = 0{,}5\]
2. Möglichkeit: Stammfunktion \(F(x)\) aus Teilaufgabe 1c verwenden
\[A = \int_{0}^{\ln{2}} f(x) = \int_{0}^{\ln{2}} 2e^{-x} \cdot \left( 2e^{-x} - 1\right) dx\]
Eine Stammfunktion der Integrandenfunktion \(f\) ist mit \(F(x) = 2e^{-x} - 2e^{-2x}; \; D_{F} = \mathbb R\) bereits gegeben (vgl. Angabe Teilaufgabe 1c).
Flächeninhalt \(A\) berechnen:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*} A &= \int_{0}^{\ln{2}} f(x) dx \\[0.8em] &= \int_{0}^{\ln{2}} 2e^{-x} \cdot \left( 2e^{-x} - 1\right) dx \\[0.8em] &= \left[ 2e^{-x} - 2e^{-2x} \right]_{0}^{\ln{2}} \\[0.8em] &= 2e^{-\ln{2}} - 2e^{-2\ln{2}} - \left( 2e^{0} - 2e^{-2 \cdot 0} \right) & &| \; n \cdot \log_{a}{b} = \log_{a}\left( b^{n} \right) \\[0.8em] &= 2e^{\ln\big( 2^{-1} \big)} - 2e^{\ln\big( 2^{-2} \big)} - (2 \cdot 1 - 2 \cdot 1) & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= 2e^\left( \frac{1}{2} \right) - 2e^{\ln\left( \frac{1}{2^{2}} \right)} - 0 & &| \; e^{\ln{x}} = x \; \left( \text{allg.:} \; a^{\log_{a}{x}} = x \right) \\[0.8em] &= 2 \cdot \frac{1}{2} - 2 \cdot \frac{1}{4} \\[0.8em] &= \frac{1}{2} \end{align*}\]
Anmerkung:
Selbst wenn die erstgenannten beiden Möglichkeiten übersehen werden, lässt sich eine Stammfunktion von \(f\) grundsätzlich bilden, allerdings mit entsprechend mehr Zeitaufwand. Die Ergänzung am Ende der Lösung zeigt eine mögliche Vorgehensweise.
Prozentuale Abweichung des Flächeninhalts \(A_{OPQ}\) vom Flächeninhalt \(A\):
\[A_{OPQ} = \ln{2}\]
\[A = \frac{1}{2}\]
\[\frac{A_{OPQ} - A}{A} \cdot 100\,\% = \frac{\ln{2} - \frac{1}{2}}{\frac{1}{2}} \cdot 100\,\% \approx 38{,}6\,\%\]
Der Flächeninhalt des Dreiecks \(OPQ\) ist um ca. 38,6 % größer als der Flächeninhalt des Flächenstücks, das der Graph der Funktion \(f\) mit den Koordinatenachsen einschließt.
Ergänzung: Flächeninhalt \(A\) berechnen inkl. Stammfunktion \(F\) bilden
Diese Ergänzung ist nicht zwingend prüfungsrelevant. Sie zeigt, dass es möglich ist, Teilaufgabe 1f zu lösen, ohne die in Teilaufgabe 1c genannte Stammfunktion \(F\) zu berücksichtigen.
\[\begin{align*}A &= \int_{0}^{\ln{2}} 2e^{-x} \cdot \left( 2e^{-x} - 1\right) dx \\[0.8em] &= \int_{0}^{\ln{2}} \left( 4e^{-2x} - 2e^{-x} \right)dx \\[0.8em] &= 4 \cdot \int_{0}^{\ln{2}} e^{-2x} dx - 2 \cdot \int_{0}^{\ln{2}} e^{-x} dx \end{align*}\]
Mithilfe der unbestimmten Integrale \(\displaystyle \int e^{x} dx = e^{x} + C\) und \(\displaystyle \int f(ax + b) dx = \frac{1}{a} \cdot F(ax + b) + C \) lässt sich jeweils eine Stammfunktion für die Integrandenfunktionen bilden.
Wichtige unbestimmte Integrale:
\[\int e^{x} dx = e^{x} + C\]
\[\int f(ax + b) dx = \frac{1}{a}F(ax +b) + C\]
Dabei ist \(F\) eine Stammfunktion von \(f\).
(vgl. Merkhilfe)
\[\int \underbrace{e^{-2x}}_{\large{f(ax\,+\,b)}} dx = \underbrace{\frac{1}{-2}}_{\large{\frac{1}{a}}} \cdot \underbrace{e^{-2x}}_{\large{F(ax\,+\,b)}} = -\frac{1}{2}e^{-2x} + C\]
\[\int \underbrace{e^{-x}}_{\large{f(ax\,+\,b)}} dx = \underbrace{\frac{1}{-1}}_{\large{\frac{1}{a}}} \cdot \underbrace{e^{-x}}_{\large{F(ax\,+\,b)}} = -e^{-x} + C\]
Damit ergibt sich:
\[\begin{align*} A &= 4 \cdot \left[-\frac{1}{2}e^{-2x}\right]_{0}^{\ln{2}} - 2 \cdot \left[-e^{-x}\right]_{0}^{\ln{2}} \\[0.8em] &= -2 \cdot \left[ e^{-2x} \right]_{0}^{\ln{2}} + 2 \cdot \left[e^{-x}\right]_{0}^{\ln{2}} \\[0.8em] &= -2 \cdot \left( e^{-2\ln{2}} - e^{-2 \cdot 0} \right) + 2 \cdot \left( e^{-\ln{2}} - e^{0} \right) & &| \; n \cdot \log_{a}{b} = \log_{a}\left( b^{n} \right) \\[0.8em] &= -2e^{\ln\big( 2^{-2} \big)} + 2 + 2e^{\ln\big( 2^{-1} \big)} - 2 & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= -2e^{\ln\left( \frac{1}{2^{2}} \right)} + 2e^{\ln\left( \frac{1}{2} \right)} & &| \; e^{\ln{x}} = x \; \left( \text{allg.:}\; a^{\log_{a}{x}} = x \right) \\[0.8em] &= (-2) \cdot \frac{1}{4} + 2 \cdot \frac{1}{2} \\[0.8em] &= \frac{1}{2} \end{align*}\]

