Der Graph der Funktion \(f \colon x \mapsto \ln{x}\) und die Normale \(N\) im Punkt \(P(e|f(e))\) schließen im ersten Quadranten mit den Koordinatenachsen ein Flächenstück mit dem Flächeninhalt \(A\) ein.
a) Skizzieren Sie den Graphen \(G_{f}\) der Funktion \(f\) sowie die Normale \(N\) und schraffieren Sie das Flächenstück mit dem Flächeninhalt \(A\).
b) Berechnen Sie den Flächeninhalt \(A\). Rechnen Sie mit exakten Werten.
a) Skizzieren von \(G_{f}\) sowie der Normale \(N\) und Schraffieren des Flächenstücks mit dem Flächeninhalt \(A\)
Vorüberlegungen:
- Die natürliche Logarithmusfunktion ist in \(\mathbb R^{+}\) definiert. Der Graph jeder Logarithmusfunktion \(x \mapsto \log_{a}{x}\) verläuft durch die Punkte \((1|0)\) und \((a|1)\). Der Graph \(G_{f}\) der natürlichen Logarithmusfunktion \(f\) verläuft also durch die Punkte \((1|0)\) und \((e|1)\). Für \(x \to 0\) strebt der Graph der natürlichen Logarithmusfunktion steil nach \(-\infty\) und nähert sich dabei der senkrechten Asymptote \(x = 0\) (\(y\)-Achse) an. Für \(x \to +\infty\) verläuft der Graph der natürlichen Logarithmusfunktion „gemächlich" gegen \(+\infty\) (vgl. Abiturskript - 1.3.1 Eigenschaften und Rechenregeln, Natürlichen Exponential- und Logarithmusfunktion).
- Die Normale \(N\) im Punkt \(P\) ist diejenige Gerade, welche auf der Tangente an den Graphen der Funktion \(f\) im Punkt \(P\) senkrecht steht (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung und Normalensteigung).
1. Graph \(G_{f}\) der Funktion \(f \colon x \mapsto \ln{x}\) skizzieren
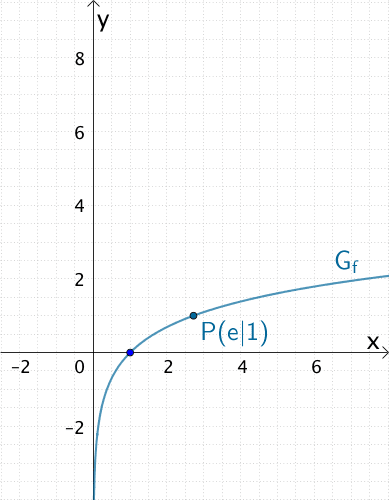
2. Tangente \(T\) an \(G_{f}\) im Punkt \(P(e|1)\) skizzieren
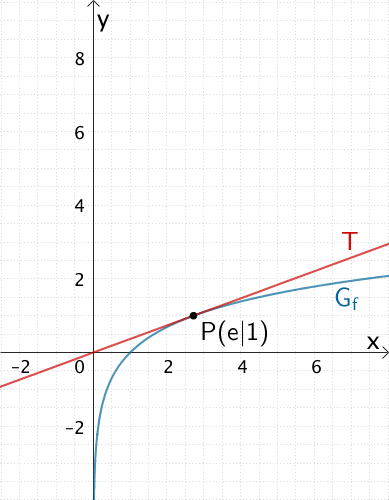
3. Normale \(N\) im Punkt \(P(e|1)\) skizzieren
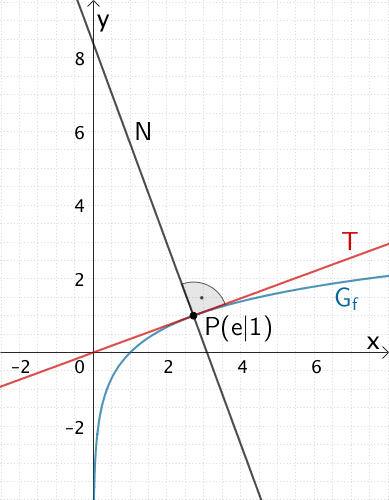
4. Flächeninhalt \(A\) schraffieren
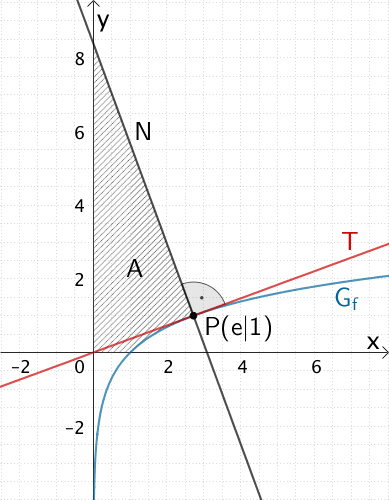
b) Berechnung des Flächeninhalts \(A\)
Da die Aufgabenstellung danach verlangt, mit exakten Werten zu rechnen, wird die Konstante \(e\) bis zur Rundung des Endergebnisses beibehalten. Zwischenergebnisse werden also als Ausdrücke von \(e\) belassen und nicht gerundet.
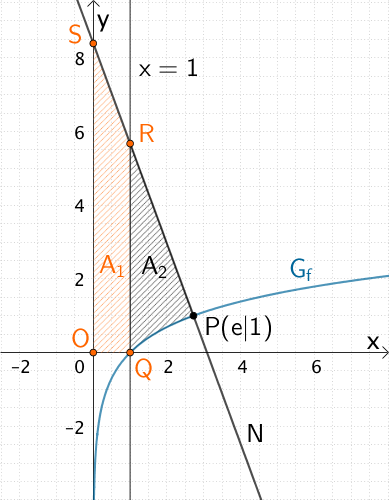
Die Gerade \(x = 1\) teilt das Flächenstück mit dem Flächeninhalt \(A\) in zwei Teilflächen mit den Flächeninhalten \(A_{1}\) und \(A_{2}\).
Dabei ist \(A_{1}\) der Flächeninhalt des Trapezes \(OQRS\) und \(A_{2}\) der Flächeninhalt der Fläche zwischen der Normale \(N\) und dem Graphen \(G_{f}\) im Intervall \([1;e]\).
Der Flächeninhalt \(A_{1}\) des Trapezes \(OQRS\) mit den parallelen Grundlinien \([OS]\) und \([QR]\) sowie der Höhe \([OQ]\) (Abstand der Grundlinien) ergibt sich zu (vgl. Merkhilfe):
\[A_{1} = \frac{\overline{OS} + \overline{QR}}{2} \cdot \overline{OQ}\]
Der Flächeninhalt \(A_{2}\) lässt sich durch Integration berechnen.
Gleichung/Funktion der Normale \(N\) bestimmen:
Der Ansatz erfolgt mit der allgemeinen Geradengleichung.
Allgemeine Geradengleichung
\[y = mx + t\]
Wobei \(m\) die Steigung und \(t\) der \(y\)-Achsenabschnitt der Geraden ist.
\[N \colon y = m_{N} \cdot x + t\]
Die Steigung \(m_{N}\) der Normale \(N\) ist gegeben durch (vgl. Merkhilfe):
Anwendung der Differetialrechnung:
Tangentensteigung und Normalensteigung
Tangentensteigung: \(m_{T} = f'(x_0)\)
Normalensteigung: \(m_{N} = -\dfrac{1}{f'(x_0)}\)
(vgl. Merkhilfe)
\[m_{N} = -\frac{1}{f'(e)}\]
Erste Ableitung \(f'\) bilden:
\[f(x) = \ln{x}; \; D_{f} = \mathbb R^{+}\]
Ableitung der natürlichen Logarithmusfunktion
\[f(x) = \ln x \enspace (x > 0) \quad \Longrightarrow \quad f'(x) = \frac{1}{x}\]
(vgl. Merkhilfe)
\[f'(x) = \frac{1}{x}\]
Somit ergibt sich die Steigung \(m_{N}\) der Normale \(N\) zu:
\[m_{N} = -\frac{1}{f'(e)} = -\frac{1}{\frac{1}{e}} = -e\]
Für die Gleichung der Normale \(N\) folgt damit:
\[N \colon y = -ex + t\]
Um den \(y\)-Achsenabschnitt \(t\) der Gleichung der Normale \(N\) zu berechnen, werden die Koordinaten des Punktes \(P(e|1) \in N\) in die Gleichung eingesetzt und diese nach \(t\) aufgelöst.
\[\begin{align*} P \in N \colon 1 &= -e \cdot e + t \\[0.8em] 1 &= -e^{2} + t &&| + e^{2} \\[0.8em] 1 + e^{2} &= t \end{align*}\]
Die Gleichung bzw. Funktion der Normale \(N\) lautet also:
\[N \colon y = -ex + 1 + e^{2}\]
\[N(x) = -ex + 1 + e^{2}\]
Damit lassen sich nun auch die Koordinaten der Punkte \(R\) und \(S\) des Trapezes \(OQRS\) berechnen bzw. angeben.

\[N(1) = -e \cdot 1 + 1 + e^{2} = 1 - e + e^{2} \quad \Longrightarrow \quad R(1|1 - e + e^{2})\]
\[S(0|1 + e^{2})\]
Flächeninhalt \(A_{1}\) des Trapezes \(OQRS\) berechnen:
\(O(0|0)\), \(Q(1|0)\), \(R(1|1- e+ e^{2})\), \(S(0|1 + e^{2})\)
\[\begin{align*}A_{1} &= \frac{\overline{OS} + \overline{QR}}{2} \cdot \overline{OQ} \\[0.8em] &= \frac{1 + e^{2} + 1 - e + e^{2}}{2} \cdot 1 \\[0.8em] &= \frac{2 - e + 2e^{2}}{2} \\[0.8em] &= e^{2} - \frac{1}{2}e + 1 \end{align*}\]
Flächeninhalt \(A_{2}\) berechnen:
(vgl. Abiturskript - 1.6.4 Flächenberechnung, Flächeninhalt zwischen zwei Funktionsgraphen)
Im Intervall \([1;e]\) gilt \(N(x) \geq f(x)\), denn die Normale N verläuft für \(x \in [1;e[\) oberhalb von \(G_{f}\) und der Punkt \(P(e|1)\) ist gemeinsamer Punkt von \(N\) und \(G_{f}\).
Um den Flächeninhalt \(A_{2}\) zu berechnen, kann also über die Differenzfunktion \(N(x) - g(x)\) mit den Integrationsgrenzen \(1\) und \(e\) integriert werden. Mit \(N(x) \geq f(x)\) kann der Betrag des Integrals entfallen.
\[f(x) = \ln{x}\]
\[N(x) = -ex + 1 + e^{2}\]
\[\begin{align*}A_{2} &= \int_{1}^{e} \left[ N(x) - f(x) \right] dx \\[0.8em] &= \int_{1}^{e} \left( -ex + 1 + e^{2} - \ln{x} \right) dx \end{align*}\]
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Für die Berechnung des bestimmten Integrals \(\displaystyle \int_{1}^{e} \left( -ex + 1 + e^{2} - \ln{x} \right) dx\) wird eine Stammfunktion der Integrandenfunktion \(x \mapsto -ex + 1 + e^{2} - \ln{x}\) benötigt.
Die Menge aller Stammfunktionen der Integrandenfunktion \(x \mapsto -ex + 1 + e^{2} - \ln{x}\) ist gegeben durch das unbestimmte Integral \(\displaystyle \int \left( -ex + 1 + e^{2} - \ln{x} \right) dx\).
Mithilfe der wichtigen unbestimmten Integrale
\(\displaystyle \int x^r \,dx = \frac{x^{r + 1}}{r + 1} + C \; (r \neq -1)\),
\(\displaystyle \int c \, dx = c \cdot x + C; \; c \in \mathbb R\) und
\(\displaystyle \int \ln x\,dx = -x + x \ln x + C\)
mit jeweils \(C \in \mathbb R\) ergibt sich:
Wichtige unbestimmte Integrale:
\[\int x^r \,dx = \frac{x^{r + 1}}{r + 1} + C \quad (r \neq -1)\]
\[\int c \, dx = c \cdot x + C; \quad c \in \mathbb R\]
\[\int \ln x\,dx = -x + x \ln x + C\]
\[C \in \mathbb R\]
(vgl. Merkhilfe)
\[\begin{align*} \int \left( -ex + 1 + e^{2} - \ln{x} \right) dx &= -\frac{e}{2}x^{2} + (1 + e^{2})x - (-x + x\ln{x}) + C \\[0.8em] &= -\frac{e}{2}x^{2} + (1 + e^{2})x + x - x\ln{x} + C \\[0.8em] &= x\left( -\frac{e}{2}x + 1 + e^{2} + 1 - \ln{x} \right) + C \\[0.8em] &= x\left( 2 + e^{2} -\frac{e}{2}x - \ln{x} \right) + C \end{align*}\]
Für \(C = 0\) ist die Funktion \(x \mapsto x\left( 2 + e^{2} -\dfrac{e}{2}x - \ln{x} \right)\) eine Stammfunktion der Integrandenfunktion \(x \mapsto -ex + 1 + e^{2} - \ln{x}\).
Damit lässt sich der Flächeninhalt \(A_{2}\) wie folgt berechnen:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*}A_{2} &= \int_{1}^{e} \left[ N(x) - f(x) \right] dx \\[0.8em] &= \int_{1}^{e} \left( -ex + 1 + e^{2} - \ln{x} \right) dx \\[0.8em] &= \left[ x\left( 2 + e^{2} -\frac{e}{2}x - \ln{x} \right) \right]_{1}^{e} \\[0.8em] &= e \cdot \left( 2 + e^{2} - \frac{e}{2} \cdot e - \ln{e} \right) - 1 \cdot \left( 2 + e^{2} - \frac{e}{2} \cdot 1 - \ln{1} \right) &&| \; \ln{e} = 1; \; \ln{1} = 0 \\[0.8em] &= e \cdot \left( 2 + e^{2} - \frac{e^{2}}{2} - 1 \right) - \left( 2 + e^{2} - \frac{e}{2} \right) \\[0.8em] &= e \cdot \left( 1 + \frac{e^{2}}{2} \right) - 2 - e^{2} + \frac{e}{2} \\[0.8em] &= e + \frac{e^{3}}{2} - 2 - e^{2} + \frac{e}{2} \\[0.8em] &= \frac{1}{2}e^{3} - e^{2} + \frac{3}{2}e - 2 \end{align*}\]
Flächeninhalt \(A\) berechnen:
\[\begin{align*}A &= A_{1} + A_{2} \\[0.8em] &= e^{2} - \frac{1}{2}e + 1 + \frac{1}{2}e^{3} - e^{2} + \frac{3}{2}e - 2 \\[0.8em] &= \frac{1}{2}e^{3} + e - 1 \\[0.8em] &\approx 11{,}76 \end{align*}\]
Der Graph \(G_{f}\) der Funktion \(f \colon x \mapsto \ln{x}\) und die Normale \(N\) im Punkt \(P(e|f(e))\) schließen im ersten Quadranten ein Flächenstück mit einem Flächeninhalt von ca. 11,76 FE (Flächeneinheiten) ein.

