Aus dem Behälter werden zwei der drei Kugeln zufällig entnommen. Ermitteln Sie die Wahrscheinlichkeit dafür, dass beide entnommenen Kugeln schwarz sind.
(3 BE)
Lösung zu Teilaufgabe b
\[\begin{align*} &\quad \; \, P(\text{„Beide entnommenen Kugeln sind schwarz"}) = \\[0.8em] &= \frac{12}{27} \cdot \frac{2}{3} \cdot \frac{1}{2} + \frac{8}{27} \cdot 1 \cdot 1 = \frac{4}{27} + \frac{8}{27} = \frac{12}{27} = \frac{4}{9}\end{align*}\]
Ausführliche Erklärung (nicht verlangt)
Die zwei entnommenen Kugeln können nur dann beide schwarz sein, wenn sich mindestens zwei schwarze Kugeln im Behälter befinden.
Aus der Lösung von Teilaufgabe a ist bekannt, dass die Wahrscheinlichkeit dafür,
dass sich zwei schwarze Kugeln im Behälter befinden, \(\textcolor{#89ba17}{\dfrac{12}{27}}\) beträgt und dafür,
dass sich drei schwarze Kugeln im Behälter befinden, \(\textcolor{#89ba17}{\dfrac{8}{27}}\) ist.
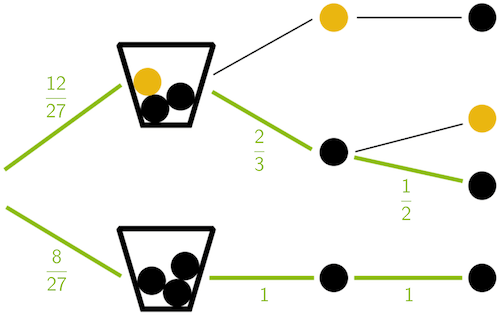
Darstellung der für das Ereignis „Beide entnommenen Kugeln sind schwarz" relevanten Pfade eines Baumdiagramms
Befinden sich zwei schwarze und eine gelbe Kugel im Behälter, beträgt die Wahrscheinlichkeit dafür, dass beide entnommenen Kugel schwarz sind \(\textcolor{#89ba17}{\dfrac{2}{3}} \cdot \textcolor{#89ba17}{\dfrac{1}{2}}\).
Befinden sich drei schwarze Kugeln im Behälter, ist die Wahrscheinlichkeit dafür, dass beide entnommenen Kugel schwarz sind \(\textcolor{#89ba17}{1} \cdot \textcolor{#89ba17}{1}\).
Mithilfe der 1. und der 2. Pfadregel ergibt sich:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*} &\quad \; \, P(\text{„Beide entnommenen Kugeln sind schwarz"}) = \\[0.8em] &= \underbrace{\underbrace{\textcolor{#89ba17}{\frac{12}{27}} \cdot \textcolor{#89ba17}{\frac{2}{3}} \cdot \textcolor{#89ba17}{\frac{1}{2}}}_{\text{1. Pfadregel}} + \underbrace{\textcolor{#89ba17}{\frac{8}{27}} \cdot \textcolor{#89ba17}{1} \cdot \textcolor{#89ba17}{1}}_{\text{1. Pfadregel}}}_{\text{2. Pfadregel}} \\[0.8em] &= \frac{4}{27} + \frac{8}{27} = \frac{12}{27} = \frac{4}{9}\end{align*}\]


