Ein Unternehmen fertigt in großer Stückzahl ein elektronisches Bauteil. Bei der Herstellung können zwei Arten von Fehlern auftreten, ein elektrischer Fehler und ein optischer Fehler. Betrachtet werden folgende Ereignisse:
\(E\): „Ein zufällig ausgewähltes Bauteil weist einen elektrischen Fehler auf."
\(O\): „Ein zufällig ausgewähltes Bauteil weist einen optischen Fehler auf."
Aus laufender Qualitätskontrolle ist bekannt, dass 5 % der gefertigten Bauteile einen elektrischen Fehler aufweisen. Zudem haben 3 % einen elektrischen, aber keinen optischen Fehler sowie 4 % einen optischen, aber keinen elektrischen Fehler.
a) Beschreiben Sie das Ereignis \(\overline{E \cup O}\) im Sachzusammenhang.
b) Erstellen Sie eine vollständig ausgefüllte Vierfeldertafel und geben Sie daraus an, mit welcher Wahrscheinlichkeit ein zufällig ausgewähltes Bauteil
α) genau einen der beiden Fehler aufweist.
β) höchstens einen der beiden Fehler aufweist.
c) Untersuchen Sie die Ereignisse \(E\) und \(O\) auf Unabhängigkeit.
d) Wie viele Bauteile müssen mindestens zufällig ausgewählt werden, um mit einer Wahrscheinlichkeit von mehr als 99 % mindestens ein Bauteil zu erhalten, das einen elektrischen Fehler aufweist?
a) Ereignis \(\overline{E \cup O}\) im Sachzusammenhang
\(E\): „Ein zufällig ausgewähltes Bauteil weist einen elektrischen Fehler auf."
\(O\): „Ein zufällig ausgewähltes Bauteil weist einen optischen Fehler auf."
Die Bedeutung des Ereignisses \(\overline{E \cup O}\) im Sachzusammenhang ist besser zu erkennen, wenn das Ereignis mithilfe des entsprechenden Gesetzes von de Morgan umformuliert wird.
Gesetze von de Morgan
Weder Ereignis \(A\) noch Ereignis \(B\); Keines der beiden Ereignisse
\[\overline{A} \cap \overline{B} = \overline{A \cup B}\]
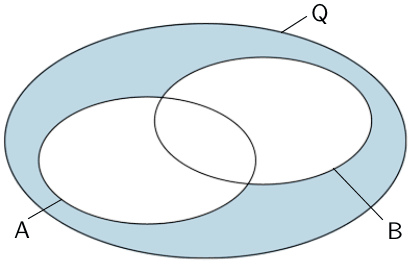
Nicht beide Ereignisse \(A\) und \(B\) zugleich; Höchstens eines der beiden Ereignisse
\[\overline{A \cap B} = \overline{A} \cup \overline{B}\]
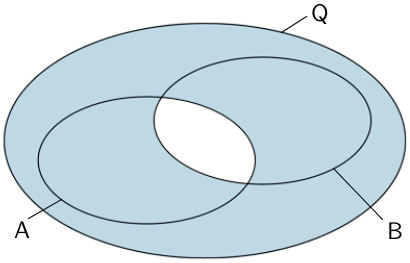
\[\overline{E \cup O} = \overline{E} \cap \overline{O}\]
\(\overline{E}\): „Ein zufällig ausgewähltes Bauteil weist keinen elektrischen Fehler auf."
\(\overline{O}\): „Ein zufällig ausgewähltes Bauteil weist keinen optischen Fehler auf."
Bedeutung des Ereignisses \(\overline{E \cup O} = \overline{E} \cap \overline{O}\) im Sachzusammenhang:
„Ein zufällig ausgewähltes Bauteil weist keinen elektrischen Fehler und keinen optischen Fehler auf."
Oder kürzer:
„Ein zufällig ausgewähltes Bauteil ist fehlerfrei."
b) Vollständig ausgefüllte Vierfeldertafel und Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes Bauteil genau einen Fehler bzw. höchstens einen der beiden Fehler aufweist
Gegeben sind folgende Wahrscheinlichkeiten:
\(P(E) = 0,05\), \(P(E \cap \overline{O}) = 0{,}03\), \(P(\overline{E} \cap O) = 0{,}04\)
Vollständig ausgefüllte Vierfeldertafel
Vierfeldertafel der Wahrscheinlichkeiten:
| \(E\) | \(\overline{E}\) | ||
| \(O\) | \(0{,}04\) | ||
| \(\overline{O}\) | \(0{,}03\) | ||
| \(0{,}05\) | \(1\) |
Vierfeldertafel der Wahrscheinlichkeiten mit den Eintragungen der gegebenen Wahrscheinlichkeiten
Die Vierfeldertafel lässt sich zeilen- bzw. spaltenweise durch Addition oder Subtraktion vervollständigen.
Mögliche Vorgehensweise:
\[P(\overline{E}) = 1 - P(E) = 1 - 0{,}05 = 0{,}95\]
\[P(E \cap O) = P(E) - P(E \cap \overline{O}) = 0{,}05 - 0{,}03 = 0{,}02\]
| \(E\) | \(\overline{E}\) | ||
| \(O\) | \(\boldsymbol{0{,}02}\) | \(0{,}04\) | |
| \(\overline{O}\) | \(0{,}03\) | ||
| \(0{,}05\) | \(\boldsymbol{0{,}95}\) | \(1\) |
\[P(O) = P(E \cap O) + P(\overline{E} \cap O) = 0{,}02 + 0{,}04 = 0{,}06\]
\[P(\overline{E} \cap \overline{O}) = P(\overline{E}) - P(\overline{E} \cap O) = 0{,}95 - 0{,}04 = 0{,}91\]
| \(E\) | \(\overline{E}\) | ||
| \(O\) | \(0{,}02\) | \(0{,}04\) | \(\boldsymbol{0{,}06}\) |
| \(\overline{O}\) | \(0{,}03\) | \(\boldsymbol{0{,}91}\) | |
| \(0{,}05\) | \(0{,}95\) | \(1\) |
\[P(\overline{O}) = 1 - P(O) = 1 - 0{,}06 = 0{,}94\]
oder
\[P(\overline{O}) = P(E \cap \overline{O}) + P(\overline{E} \cap \overline{O}) = 0{,}03 + 0{,}91 = 0{,}94\]
| \(E\) | \(\overline{E}\) | ||
| \(O\) | \(0{,}02\) | \(0{,}04\) | \(0{,}06\) |
| \(\overline{O}\) | \(0{,}03\) | \(0{,}91\) | \(\boldsymbol{0{,}94}\) |
| \(0{,}05\) | \(0{,}95\) | \(1\) |
α) Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes Bauteil genau einen Fehler der beiden Fehler aufweist
Ein zufällig ausgewähltes Bauteil darf entweder nur einen elektrischen Fehler \((E \cap \overline{O})\) oder nur einen optischen Fehler \((\overline{E} \cap O)\) aufweisen, aber nicht beide Fehler zugleich.
\[P(\text{„genau einen der beiden Fehler"}) = P(E \cap \overline{O}) + P(\overline{E} \cap O)\]
| \(E\) | \(\overline{E}\) | ||
| \(O\) | \(0{,}02\) | \(\boldsymbol{0{,}04}\) | \(0{,}06\) |
| \(\overline{O}\) | \(\boldsymbol{0{,}03}\) | \(0{,}91\) | \(0{,}94\) |
| \(0{,}05\) | \(0{,}95\) | \(1\) |
Mithilfe der Vierfeldertafel ergibt sich:
\[\begin{align*}P(\text{„genau einen der beiden Fehler"}) &= P(E \cap \overline{O}) + P(\overline{E} \cap O) \\[0.8em] &= 0{,}03 + 0{,}04 \\[0.8em] &= 0{,}07 \\[0.8em] &= 7\,\% \end{align*}\]
β) Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes Bauteil höchstens einen der beiden Fehler aufweist
Ein zufällig ausgewähltes Bauteil darf fehlerfrei sein \(\overline{E} \cap \overline{O}\) oder nur einen elektrischen Fehler \((E \cap \overline{O})\) haben oder nur einen optischen Fehler \((\overline{E} \cap O)\) haben. Das Ereignis „höchstens einen der beiden Fehler" entspricht der Vereinigungsmenge \(\overline{E} \cup \overline{O}\).
\[\begin{align*}P(\text{„höchstens einen der beiden Fehler"}) &= P(\overline{E} \cap \overline{O}) + P(E \cap \overline{O}) + P(\overline{E} \cap O) \\[0.8em] &= P(\overline{E} \cup \overline{O}) \end{align*}\]
| \(E\) | \(\overline{E}\) | ||
| \(O\) | \(0{,}02\) | \(\boldsymbol{0{,}04}\) | \(0{,}06\) |
| \(\overline{O}\) | \(\boldsymbol{0{,}03}\) | \(\boldsymbol{0{,}91}\) | \(0{,}94\) |
| \(0{,}05\) | \(0{,}95\) | \(1\) |
Mithilfe der Vierfeldertafel ergibt sich:
\[\begin{align*}P(\text{„höchstens einen der beiden Fehler"}) &= P(\overline{E} \cap \overline{O}) + P(E \cap \overline{O}) + P(\overline{E} \cap O) \\[0.8em] &= 0{,}91 + 0{,}03 + 0{,}04 \\[0.8em] &= 0{,}98 \\[0.8em] &= 98\,\% \end{align*}\]
oder
\[\begin{align*}P(\text{„höchstens einen der beiden Fehler"}) &= P(\overline{E} \cap \overline{O}) + P(E \cap \overline{O}) + P(\overline{E} \cap O) \\[0.8em] &= P(\overline{E} \cup \overline{O}) \\[0.8em] &= 1 - P(E \cap O) \\[0.8em] &= 1 - 0{,}02 \\[0.8em] &= 0{,}98 \\[0.8em] &= 98\,\% \end{align*}\]
c) Untersuchung der Ereignisse \(E\) und \(O\) auf Unabhängigkeit
Die Ereignisse \(E\) und \(O\) sind stochastisch unabhängig, wenn beispielsweise (vgl. Anmerkung unten) folgende Bedingung erfüllt ist:
Stochastische (Un)Abhängigkeit von zwei Ereignissen
Zwei Ereignisse \(A\) und \(B\) heißen stochastisch unabhängig, wenn
\(P(A) \cdot P(B) = P(A \cap B)\) gilt. (vgl. Merkhilfe) *
Andernfalls heißen die Ereignisse \(A\) und \(B\) stochastisch abhängig.
Sind zwei Ereignisse \(A\) und \(B\) stochastisch unabhängig, beeinflusst das Eintreten des Ereignisses \(A\) nicht das Eintreten des Ereignisses \(B\) und umgekehrt.
* Oder wenn
\(P(\overline{A}) \cdot P(B) = P(\overline{A} \cap B)\) bzw.
\(P(A) \cdot P(\overline{B}) = P(A \cap \overline{B})\) bzw.
\(P(\overline{A}) \cdot P(\overline{B}) = P(\overline{A} \cap \overline{B})\) gilt.
\[P(E) \cdot P(O) = P(E \cap O)\]
| \(E\) | \(\overline{E}\) | ||
| \(O\) | \(\boldsymbol{0{,}02}\) | \(0{,}04\) | \(\boldsymbol{0{,}06}\) |
| \(\overline{O}\) | \(0{,}03\) | \(0{,}91\) | \(0{,}94\) |
| \(\boldsymbol{0{,}05}\) | \(0{,}95\) | \(1\) |
Mithilfe der Vierfeldertafel ergibt sich:
\(P(E \cap O) = 0{,}02\)
\(P(E) = 0{,}05\), \(P(O) = 0{,}06\)
\[P(E) \cdot P(O) = 0{,}05 \cdot 0{,}06 = 0{,}003\]
\[\Longrightarrow \quad P(E) \cdot P(O) \neq P(E \cap O)\]
\(\Longrightarrow \quad\)Die Ereignisse \(E\) und \(O\) sind stochastisch abhängig.
Anmerkung:
Im Falle zweier stochastisch unabhängiger Ereignisse \(A\) und \(B\) gilt:
\(P(A \cap B) = P(A) \cdot P(B)\) und
\(P(\overline{A} \cap B) = P(\overline{A}) \cdot P(B)\) und
\(P(A \cap \overline{B}) = P(A) \cdot P(\overline{B})\) und
\(P(\overline{A} \cap \overline{B}) = P(\overline{A}) \cdot P(\overline{B})\).
Die aus Teilaufgabe b vorliegende vollständig ausgefüllte Verfeldertafel liefert demnach drei weitere Möglichkeiten, die Unabhängigkeit der Ereignisse \(E\) und \(O\) zu überprüfen.
d) Anzahl der mindestens zufällig auszuwählenden Bauteile, um mit einer Wahrscheinlichkeit von mehr als 99 % mindestens ein Bauteil zu erhalten, das einen elektrischen Fehler aufweist
Mindestens ein Bauteil von \(n\) ausgewählten Bauteilen soll einen elektrischen Fehler haben.
Das Ereignis „Mindestens ein Bauteil von \(n\) ausgewählten Bauteilen hat einen elektrischen Fehler" kann durch die Verneinung des Gegenereignisses „Kein Bauteil von \(n\) ausgewählten Bauteilen hat einen elektrischen Fehler" ausgedrückt werden. Man betrachtet also die Wahrscheinlichkeit des Ereignisses „Nicht kein Bauteil von \(n\) ausgewählten Bauteilen hat einen elektrischen Fehler". Diese Wahrscheinlichkeit soll größer als 99 % sein (vgl. Angabe).
Mit \(P(\overline{E}) = 0{,}95\) (vgl. Teilaufgabe b) formuliert man folgenden Ansatz:
\[\begin{align*}\underbrace{1 - \underbrace{\left[P(\overline{E})\right]^{n}}_{\large{n\text{-mal kein elektrischer Fehler}}}}_{\large{\text{nicht}\;n\text{-mal kein elektrischer Fehler}}} &> 0{,}99 \\[0.8em] 1 - 0{,}95^{n} &> 0{,}99\end{align*}\]
Elementares Umformen führt auf eine Exponentialungleichung, die sich durch Logarithmieren (beliebige Basis, z.B. \(\ln\)) und weitere Umformungen lösen lässt. Dabei ist darauf zu achten, dass sich das Relationszeichen der Ungleichung bei einer Multiplikation/Division mit/durch eine(r) negativen Zahl umkehrt.
\[\begin{align*}1 - 0{,}95^{n} &> 0{,}99 & &| - 1 \\[0.8em] -0{}95^{n} &> -0{,}01 & &| \cdot (-1)\; \text{Relationszeichen dreht!} \\[0.8em] 0{,}95^{n} &< 0{,}01 & &| \; \ln \; \text{(Logarithmieren)} \\[0.8em] \ln\left( 0{,}95^{n}\right) &< \ln{0{,}01} & &| \; \log_{a}{b^{n}} = n \cdot \log_{a}{b} \\[0.8em] n \cdot \ln{0{,}95} &< \ln{0{,}01} & &| : \ln{0{,}95} \; \text{Relationszeichen dreht!} \\[0.8em] n &> \frac{\ln{0{,}01}}{\ln{0{,}95}} \\[0.8em] n &\gtrsim 89{,}78 & &| \; n \in \mathbb N\end{align*}\]
\[\Longrightarrow \quad n = 90\]
Es müssen mindestens 90 Bauteile zufällig ausgewählt werden, um mit einer Wahrscheinlichkeit von mehr als 99 % mindestens ein Bauteil zu erhalten, das einen elektrischen Fehler aufweist.

