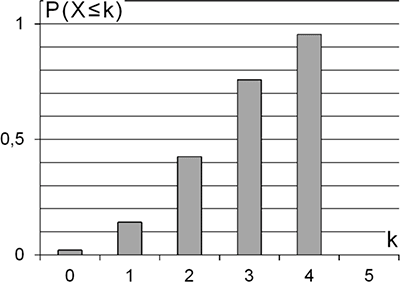
Gegeben ist eine binomialverteilte Zufallsgröße \(X\) mit dem Parameterwert \(n = 5\). Dem Diagramm in Abbildung 1 kann man die Wahrscheinlichkeitswerte \(P(X \leq k)\) mit \(k \in \{0; 1; 2; 3; 4\}\) entnehmen.
Ergänzen Sie den zu \(k = 5\) gehörenden Wahrscheinlichkeitswert im Diagramm. Ermitteln Sie näherungsweise die Wahrscheinlichkeit \(P(X = 2)\).
(2 BE)
Lösung zu Teilaufgabe 2
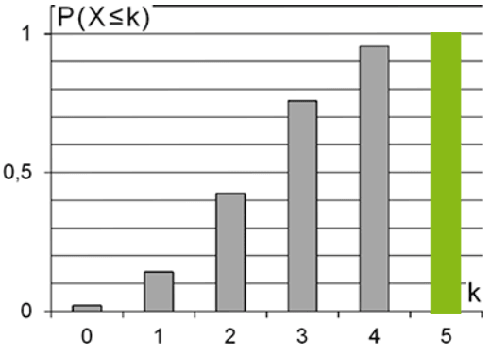
Ergänzung des zu \(k = 5\) gehörenden Wahrscheinlichkeitswerts
Abbildung 1 zeigt ein Balkendiagramm der aufsummierten Wahrscheinlichkeiten \(P(X \leq k)\) der nach \(B(5;p)\) binomialverteilten Zufallsgröße \(X\), das heißt ein Balkendiagramm der kumulativen Verteilungsfunktion von \(X\).
Kumulative Verteilungsfunktion einer nach \(B(n, p)\) binomialverteilten Zufallsgröße \(X\)
\[F^n_p (k) = P^n_p (X \leq k) = \sum_{i \, = \, 0}^k B(n; p; i) = \sum_{i \, = \, 0}^k \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i}\]
Wobei \(n\) die Länge der Bernoullikette, \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses und \(k \in \{0,1,\dots,n\}\) die Anzahl der Treffer ist.
Das Stochastische Tafelwerk (ST) listet die Werte der Kumulativen Verteilungsfunktion jeweils in der rechten Spalte einer betrachteten Tabelle der Parameter \(n\) und \(p\).
Da die Summe der Wahrscheinlichkeiten aller Werte der Zufallsgröße \(X\) gleich Eins ist, gilt für \(k = n = 5\):
\[P^{5}_{p}(X \leq 5) = \sum \limits_{I\,=\,0}^{k\,=\,5}B(5; p; i) = \textcolor{#89ba17}{1}\]
Nährungsweise Bestimmung der Wahrscheinlichkeit \(P(X = 2)\)
\[\begin{align*}P(X = 2) &= P(X \leq 2) - P(X \leq 1) \\[0.8em] &\approx \underbrace{0{,}41 - 0{,}14}_{\text{aus Diagramm abgelesen}} \\[0.8em] &= 0{,}27 \end{align*}\]


