Von der Boje aus taucht der Fotograf senkrecht bezüglich der Wasseroberfläche nach unten bis zu einer Stelle, deren Abstand zum Meeresboden genau drei Meter beträgt und im Modell durch den Punkt \(K\) dargestellt wird.
Bestimmen Sie rechnerisch, welche Tiefe unter der Wasseroberfläche der Fotograf bei diesem Tauchvorgang erreicht.
(5 BE)
Lösung zu Teilaufgabe f
1. Möglichkeit: Hesseschen Normalenform der Ebene E anwenden
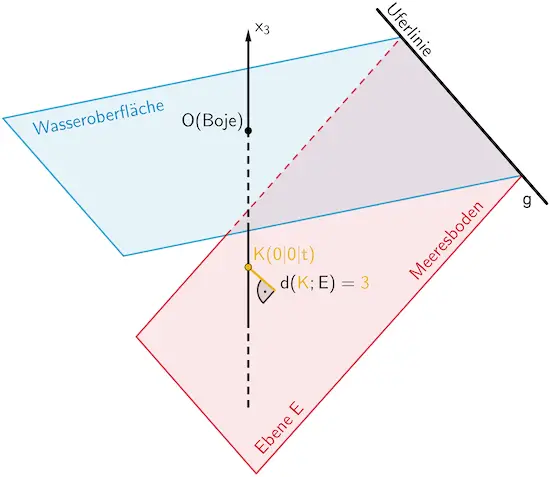
Planskizze (optional): Da der Punkt \(K\) unterhalb des Koordinatenursprungs \(O\) auf der \(x_3\)-Achse liegt, sind dessen \(x_1\)- und \(x_2\)-Koordinate gleich null. Beispielsweise wählt man \(\textcolor{#e9b509}{K(0|0|t)}\) mit \(t \in \mathbb R\). Damit ist der Ansatz \(d(\textcolor{#e9b509}{K};E) = \textcolor{#e9b509}{3}\) mithilfe der Hesseschen Normalenform der Ebene \(E\) zielführend (weil nur die eine Unbekannte \(t\) zu bestimmen ist).
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
Hessesche Normalenform der Ebene \(E\) formulieren:
\(E \colon 2x_1 - x_2 + 2x_3 + 35 = 0\) (vgl. Teilaufgabe b)
\[E \colon \frac{\textcolor{#cc071e}{2}x_1 \textcolor{#cc071e}{-} x_2 + \textcolor{#cc071e}{2}x_3 + 35}{\sqrt{\textcolor{#cc071e}{2}^2 + \textcolor{#cc071e}{(-1)}^2 + \textcolor{#cc071e}{2}^2}} = 0 \enspace \text{(HNF)}\]
\[E \colon \frac{2x_1 - x_2 + 2x_3 + 35}{3} = 0 \enspace \text{(HNF)}\]
Somit gilt für den Abstand \(d(\textcolor{#e9b509}{K};E)\):
\[d(\textcolor{#e9b509}{K};E) = \left| \frac{2\textcolor{#e9b509}{k_1} - \textcolor{#e9b509}{k_2} + 2\textcolor{#e9b509}{k_3} + 35}{3} \right|\]
Tauchtiefe des Fotografen berechnen:
\(\textcolor{#e9b509}{K(0|0|t)}\) mit \(t \in \mathbb R\)
\[\begin{align*}d(\textcolor{#e9b509}{K};E) &= \textcolor{#e9b509}{3} \\[0.8em] \left| \frac{2\textcolor{#e9b509}{k_1} - \textcolor{#e9b509}{k_2} + 2\textcolor{#e9b509}{k_3} + 35}{3} \right| &= \textcolor{#e9b509}{3} \\[0.8em] \left| \frac{ 2 \cdot \textcolor{#e9b509}{0} - \textcolor{#e9b509}{0} + 2 \cdot \textcolor{#e9b509}{t} + 35}{3} \right| &= \textcolor{#e9b509}{3} \\[0.8em] \frac{\vert 2t + 35 \vert}{3} &= 3 &&| \cdot 3 \\[0.8em] \vert 2t + 35 \vert &= 9 \end{align*}\]
Die Betragsgleichung wird durch Fallunterscheidung gelöst:
(vgl. Abiturskript - 1.1.5 Betragsfunktion, Betragsgleichungen)
1. Fall: \(2t + 35 \textcolor{#cc071e}{\geq} 0\)
Die Betragsstriche können entfallen und es folgt:
\[\begin{align*}2t + 35 &= 9 &&| - 35 \\[0.8em] 2t &= -26 &&| : 2 \\[0.8em] t &= -13\end{align*}\]
2. Fall: \(2t + 35 \textcolor{#cc071e}{<} 0\)
Der Term \(\textcolor{#cc071e}{-}(2t + 35)\) ersetzt den Betrag und es folgt:
\[\begin{align*}-(2t + 35) &= 9 \\[0.8em] -2t -35 &= 9 &&| + 35 \\[0.8em] -2t &= 44 &&| : (-2) \\[0.8em] t &= -22\end{align*}\]
Um zu prüfen, welcher der Werte von \(t\) im Sachzusammenhang sinnvoll ist, setzt man die Koordinaten von \(K(0|0|t)\) in die Gleichung der Ebene \(E\) (Meeresboden) ein und erhält zum Vergleich denjenigen Wert für \(t\), der im Modell der Meerestiefe unterhalb der Boje (Koordinatenursprung) entspricht.
\(\textcolor{#e9b509}{K(0|0|t)}\) mit \(t \in \mathbb R\)
\(E \colon 2x_1 - x_2 + 2x_3 + 35 = 0\)
\[2 \cdot \textcolor{#e9b509}{0} - \textcolor{#e9b509}{0} + 2 \cdot \textcolor{#e9b509}{t} + 35 = 0 \enspace \Leftrightarrow \enspace t = -17{,}5\]
Damit kommt der Wert \(t = -22\) nicht in Frage, da dieser einer Tiefe unterhalb des Meeresbodens (Ebene \(E\)) entspricht. Die im Sachzusammenhang korrekte Lösung ist also \(t = -13\).
Der Fotograf erreicht bei seinem Tauchvorgang eine Tiefe von 13 m.
2. Möglichkeit: Parallele Hilfsebene zu Ebene E aufstellen
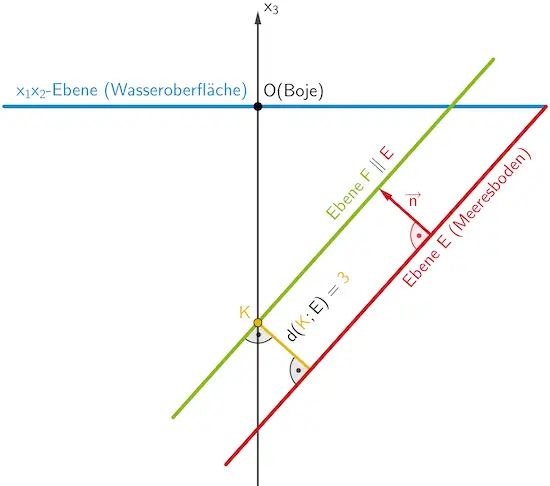
Planskizze (optional): Der Normalenvektor \(\textcolor{#cc071e}{\overrightarrow{n} = \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix}}\) der Ebene \(\textcolor{#cc071e}{E}\) (vgl. Teilaufgabe b) hat die Länge \(\textcolor{#cc071e}{\vert \overrightarrow{n} \vert} = \sqrt{2^2 + (-1)^2 + 2^2} \textcolor{#cc071e}{= 3}\).
Die Ebene \(\textcolor{#89ba17}{F}\) entsteht durch Verschiebung der Ebene \(\textcolor{#cc071e}{E}\) um den Normalenvektor \(\textcolor{#cc071e}{\overrightarrow{n}}\). Sie verläuft im Abstand 3 parallel zur Ebene \(\textcolor{#cc071e}{E}\) und schneidet die \(x_3\)-Achse im Punkt \(\textcolor{#e9b509}{K}\). Die \(\textcolor{#e9b509}{x_3}\)-Koordinate von \(\textcolor{#e9b509}{K}\) entspricht der Tiefe, die der Fotograf bei seinem Tauchgang erreicht.
Gleichung der Ebene \(\textcolor{#89ba17}{F} \parallel \textcolor{#cc071e}{E}\) mit \(d(\textcolor{#89ba17}{F};\textcolor{#cc071e}{E}) = \textcolor{#e9b509}{3}\) bestimmen:
Wegen \(\textcolor{#89ba17}{F} \parallel \textcolor{#cc071e}{E}\) ist der Normalenvektor \(\textcolor{#cc071e}{\overrightarrow{n} = \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix}}\) der Ebene \(\textcolor{#cc071e}{E}\) auch ein Normalenvektor der Ebene \(\textcolor{#89ba17}{F}\)
\(\textcolor{#cc071e}{E}\colon \textcolor{#cc071e}{2}x_1 \textcolor{#cc071e}{-} x_2 + \textcolor{#cc071e}{2}x_3 + 35 = 0\) (vgl. Teilaufgabe b)
\(\textcolor{#89ba17}{F} \parallel \textcolor{#cc071e}{E} \enspace \Rightarrow \enspace \textcolor{#89ba17}{F}\colon \textcolor{#cc071e}{2}x_1 \textcolor{#cc071e}{-} x_2 + \textcolor{#cc071e}{2}x_3 + \boldsymbol{n_0} = 0\)
Um den Wert von \(\boldsymbol{n_0}\) zu bestimmen, sodass die Ebene \(\textcolor{#89ba17}{F}\) im Abstand 3 parallel zur Ebene \(\textcolor{#cc071e}{E}\) verläuft, wird ein Punkt der Ebene \(\textcolor{#cc071e}{E}\), beispielsweise Punkt \(P(4|5|-19)\) (vgl. Angabe) um den Normalenvektor von \(\textcolor{#cc071e}{E}\) verschoben (Vektoraddition) und die Koordinaten des Bildpunktes \(\textcolor{#89ba17}{P'}\) in die Gleichung der Ebene \(\textcolor{#89ba17}{F}\) eigesetzt.
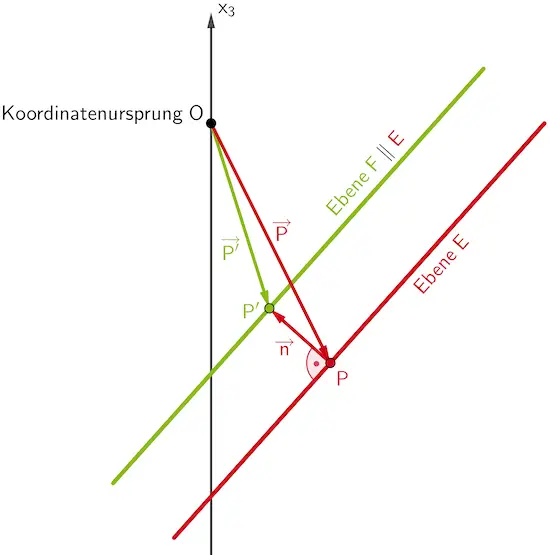(Skizze schematisch, nicht verlangt)
\(\textcolor{#cc071e}{P(4|5|-19)} \in \textcolor{#cc071e}{E}\), \(\textcolor{#89ba17}{P'} \in \textcolor{#89ba17}{F}\)
\[\textcolor{#cc071e}{\overrightarrow{n} = \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix}}\]
\[\begin{align*} \textcolor{#89ba17}{\overrightarrow{P'}} &= \textcolor{#cc071e}{\overrightarrow{P}} + \textcolor{#cc071e}{\overrightarrow{n}} \\[0.8em] &= \textcolor{#cc071e}{\begin{pmatrix} 4 \\ 5 \\ -19 \end{pmatrix}} + \textcolor{#cc071e}{\begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix}} \\[0.8em] &= \textcolor{#89ba17}{\begin{pmatrix} 6 \\ 4 \\ -17 \end{pmatrix}}\end{align*}\]
\[\begin{align*}\textcolor{#89ba17}{P'} \in \textcolor{#89ba17}{F}\colon 2 \cdot \textcolor{#89ba17}{6} - \textcolor{#89ba17}{4} + 2 \cdot \textcolor{#89ba17}{(-17)} + n_0 &= 0 \\[0.8em] 12 - 4 - 34 + n_0 &= 0 \\[0.8em] -26 + n_0 &= 0 &&| + 26 \\[0.8em] n_0 = 26\end{align*}\]
\[\Rightarrow \enspace \textcolor{#89ba17}{F}\colon 2x_1 - x_2 + 2x_3 + 26 = 0\]
Schnittpunkt \(\textcolor{#e9b509}{K}\) der Ebene \(\textcolor{#89ba17}{F}\) mit der \(x_3\)-Achse bestimmen:
Da der Punkt \(\textcolor{#e9b509}{K}\) unterhalb des Koordinatenursprungs \(O\) auf der \(x_3\)-Achse liegt, sind dessen \(x_1\)- und \(x_2\)-Koordinate gleich null. Beispielsweise wählt man \(\textcolor{#e9b509}{K(0|0|t)}\) mit \(t \in \mathbb R\).
\[\begin{align*}\textcolor{#e9b509}{K(0|0|t)} \in \textcolor{#89ba17}{F} \colon 2 \cdot \textcolor{#e9b509}{0} - \textcolor{#e9b509}{0} + 2 \cdot \textcolor{#e9b509}{t} + 26 &= 0 \\[0.8em] 2t + 26 &= 0 &&| - 26 \\[0.8em] 2t &= -26 &&| : 2 \\[0.8em] t &= -13\end{align*}\]
Der Fotograf erreicht bei seinem Tauchvorgang eine Tiefe von 13 m.
3. Möglichkeit: Elementargeometrisch, Trigonometrie im rechtwinkligen Dreieck
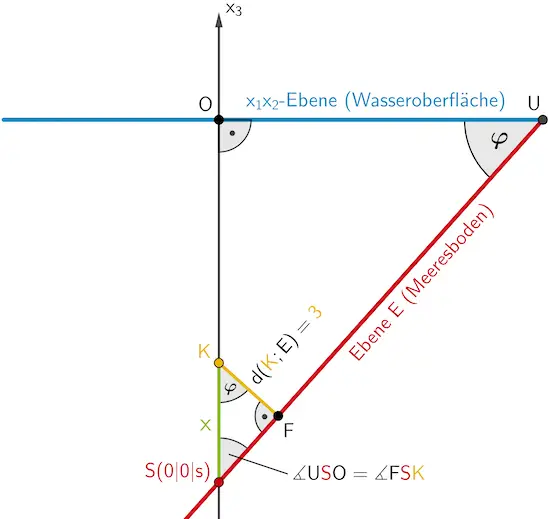
Planskizze (optional): Schnittwinkel \(\boldsymbol{\varphi}\) zwischen der \(x_1x_2\)-Ebene und der Ebene \(E\) (vgl. Teilaufgabe c)
Die beiden rechtwinkligen Dreiecke \(\textcolor{#cc071e}{S}UO\) und \(\textcolor{#cc071e}{S}F\textcolor{#e9b509}{K}\) haben den gemeinsamen Winkel \(\measuredangle U\textcolor{#cc071e}{S}O = \measuredangle F\textcolor{#cc071e}{S}\textcolor{#e9b509}{K}\).
Deshalb gilt im Dreieck \(\textcolor{#cc071e}{S}F\textcolor{#e9b509}{K}\): \(\measuredangle \textcolor{#cc071e}{S}\textcolor{#e9b509}{K}F = \boldsymbol{\varphi}\).
Damit lässt sich im Dreieck \(\textcolor{#cc071e}{S}F\textcolor{#e9b509}{K}\) die Länge \(\textcolor{#89ba17}{x}\) der Seite \([\textcolor{#cc071e}{S}\textcolor{#e9b509}{K}]\) berechnen. Addiert man diese zur \(x_3\)-Koordinate des Schnittpunkts \(\textcolor{#cc071e}{S}\) der Ebene \(\textcolor{#cc071e}{E}\) mit der \(x_3\)-Achse, so erhält man die \(\textcolor{#e9b509}{x_3}\)-Koordinate des Punktes \(\textcolor{#e9b509}{K}\), welche der Tiefe entsprich, die der Fotograf bei seinem Tauchgang erreicht.
Schnittpunkt \(\textcolor{#cc071e}{S}\) der Ebene \(\textcolor{#cc071e}{E}\) mit der \(x_3\)-Achse bestimmen:
Da \(\textcolor{#cc071e}{S}\) auf der \(x_3\)-Achse liegt, sind dessen \(x_1\)- und \(x_2\)-Koordinate gleich null.
\[\textcolor{#cc071e}{S(0|0|s)}\]
\[\textcolor{#cc071e}{E}\colon2x_1 - x_2 + 2x_3 + 35 = 0\]
\[\textcolor{#cc071e}{S(0|0|s) \in E} \colon 2 \cdot \textcolor{#cc071e}{0} - \textcolor{#cc071e}{0} + 2 \cdot \textcolor{#cc071e}{s} + 35 = 0 \enspace \Leftrightarrow \enspace \textcolor{#cc071e}{s} = \textcolor{#cc071e}{-17{,}5}\]
Länge \(\textcolor{#89ba17}{x}\) der Seite \([\textcolor{#cc071e}{S}\textcolor{#e9b509}{K}]\) im Dreieck \(\textcolor{#cc071e}{S}F\textcolor{#e9b509}{K}\) berechnen:
Ergebnis aus Teilaufgabe c: \(\cos{\varphi} = \dfrac{2}{3}\)
Trigonometrische Beziehungen im rechtwinkligen Dreieck (vgl. Merkhilfe)
\[\sin \alpha = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}\]
\[\cos \alpha = \frac{\text{Ankathete}}{\text{Hypotenuse}}\]
\[\tan \alpha = \frac{\text{Gegenkathete}}{\text{Ankathete}}\]
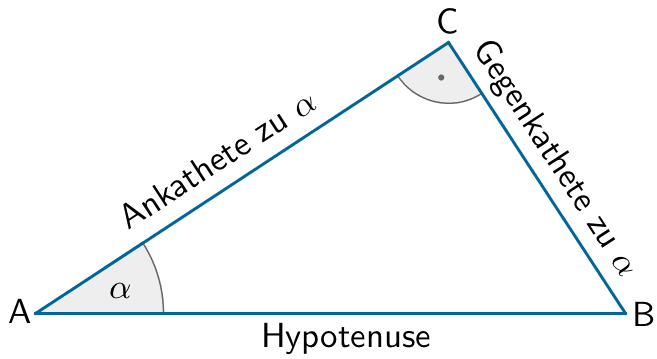
\[\cos{\varphi} = \frac{\textcolor{#e9b509}{3}}{\textcolor{#89ba17}{x}} \enspace \Leftrightarrow \enspace \textcolor{#89ba17}{x} = \frac{\textcolor{#e9b509}{3}}{\cos{\varphi}} = \frac{3}{\frac{2}{3}} = 3 \cdot \frac{3}{2} = \frac{9}{2} = \textcolor{#89ba17}{4{,}5}\]
\(\textcolor{#e9b509}{x_3}\)-Koordinate von \(\textcolor{#e9b509}{K}\) berechnen:
\[\textcolor{#cc071e}{s} + \textcolor{#89ba17}{x} = \textcolor{#cc071e}{-17{,}5} + \textcolor{#89ba17}{4{,}5} = \textcolor{#e9b509}{-13}\]
Der Fotograf erreicht bei seinem Tauchvorgang eine Tiefe von 13 m.
