Die Punkte \(A(3|-1|5)\), \(B(5|3|1)\) und \(C(7|-3|9)\) legen das Dreieck \(ABC\) fest.
a) Weisen Sie nach, dass das Dreieck \(ABC\) gleichschenklig ist.
b) Berechnen Sie die Maßzahl des Flächeninhalts des Dreiecks \(ABC\).
c) Berechnen Sie die Koordinaten des Punktes \(D\), der das Dreieck \(ABC\) zu einer Raute ergänzt.
d) Berechnen Sie den Winkel \(\measuredangle{DBA} = \varphi\).
e) Der Punkt \(S(4,6,10)\) ist die Spitze der Pyramide \(ABCS\), deren Grundfläche das Dreieck \(ABC\) ist. Weisen Sie nach, dass die Strecke \([MS]\) des Mittelpunkts \(M\) der Grundkante \([BC]\) und der Pyramidenspitze \(S\) die Höhe der Pyramide \(ABCS\) ist.
f) Berechnen Sie die Maßzahl des Volumens der Pyramide \(ABCS\).
a) Nachweis, dass das Dreieck \(ABC\) gleichschenklig ist
Das Dreieck \(ABC\) ist gleichschenklig, wenn genau zwei Seiten des Dreiecks gleich lang sind.
Länge der Seite \([AB]\), \([AC]\) und \([BC]\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \overline{AB} &= \vert \overrightarrow{AB} \vert \\[0.8em] &= \vert \overrightarrow{B} - \overrightarrow{A} \vert \\[0.8em] &= \left| \begin{pmatrix} 5 \\ 3 \\ 1 \end{pmatrix} - \begin{pmatrix} 3 \\ -1 \\ 5 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 2 \\ 4 \\ -4 \end{pmatrix} \right| \\[0.8em] &= \sqrt{2^{2} + 4^{2} + (-4)^{2}} \\[0.8em] &= \sqrt{36} \\[0.8em] &= 6 \end{align*}\]
\[\begin{align*} \overline{AC} &= \vert \overrightarrow{AC} \vert \\[0.8em] &= \vert \overrightarrow{C} - \overrightarrow{A} \vert \\[0.8em] &= \left| \begin{pmatrix} 7 \\ -3 \\ 9 \end{pmatrix} - \begin{pmatrix} 3 \\ -1 \\ 5 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 4 \\ -2 \\ 4 \end{pmatrix} \right| \\[0.8em] &= \sqrt{4^{2} + (-2)^{2} + 4^{2}} \\[0.8em] &= \sqrt{36} \\[0.8em] &= 6 \end{align*}\]
\[\begin{align*} \overline{BC} &= \vert \overrightarrow{BC} \vert \\[0.8em] &= \vert \overrightarrow{C} - \overrightarrow{B} \vert \\[0.8em] &= \left| \begin{pmatrix} 7 \\ -3 \\ 9 \end{pmatrix} - \begin{pmatrix} 5 \\ 3 \\ 1 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 2 \\ -6 \\ 8 \end{pmatrix} \right| \\[0.8em] &= \sqrt{2^{2} + (-6)^{2} + 8^{2}} \\[0.8em] &= \sqrt{104} \\[0.8em] &= 2\sqrt{26} \\[0.8em] &\approx 10{,}2 \end{align*}\]
\[\Longrightarrow \quad \overline{AB} = \overline{AC} \neq \overline{BC}\]
Das Dreieck \(ABC\) ist gleichschenklig mit der Basis \([BC]\).
b) Maßzahl des Flächeninhalts des Dreiecks \(ABC\)
Die Maßzahl des Flächeninhalts des Dreiecks \(ABC\) ist gleich der Hälfte des Betrags des Vektorprodukts der Verbindungsvektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\).
Anwendung des Vekorprodukts
Der Betrag des Vektorprodukts \(\overrightarrow{a} \times \overrightarrow{b}\) entspricht der Maßzahl des Flächeninhalts eines von zwei Vektoren \(\overrightarrow{a} \neq \overrightarrow{0}\) und \(\overrightarrow{b} \neq \overrightarrow{0}\) aufgespannten Parallelogramms.
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \textcolor{#cc071e}{\vert \overrightarrow{b} \vert \cdot \sin{\varphi}}\]
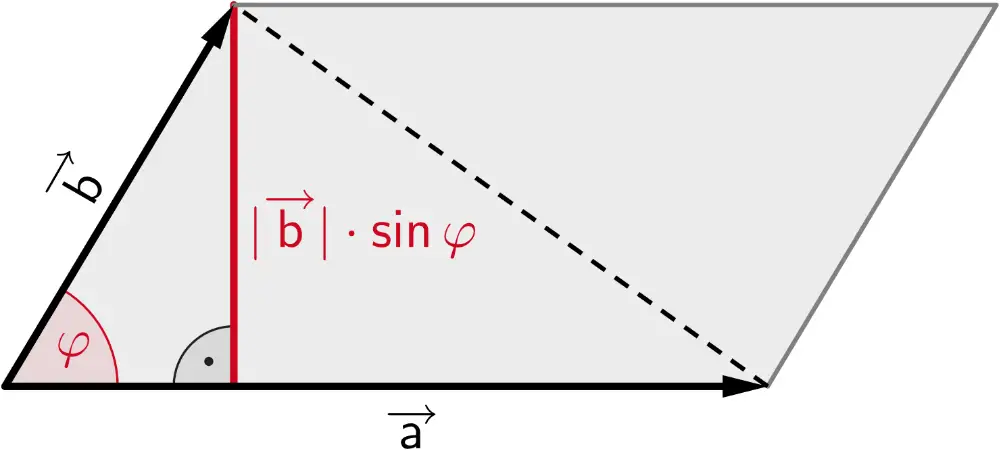
Flächeninhalt eines Parallelogramms
\[A = \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
Flächeninhalt eines Dreiecks
\[A = \frac{1}{2} \cdot \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
\(\overrightarrow{AB} = \begin{pmatrix} 2 \\ 4 \\ -4 \end{pmatrix}\), \(\overrightarrow{AC} = \begin{pmatrix} 4 \\ -2 \\ 4 \end{pmatrix}\) (vgl. Teilaufgabe a)
\[\begin{align*} A_{ABC} &= \frac{1}{2} \cdot \vert \overrightarrow{AB} \times \overrightarrow{AC} \vert \\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} 2 \\ 4 \\ -4 \end{pmatrix} \times \begin{pmatrix} 4 \\ -2 \\ 4 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} 4& \cdot & 4 & - & (-4) & \cdot & (-2) \\ (-4) & \cdot & 4 & - & 2 & \cdot & 4 \\ 2 & \cdot & (-2) & - & 4 & \cdot & 4 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} 8 \\ -24 \\ -20 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \sqrt{8^{2} + (-24)^{2} + (-20)^{2}} \\[0.8em] &= \frac{1}{2} \cdot \sqrt{1040} \\[0.8em] &= 2\sqrt{65} \\[0.8em] &\approx 16{,}12 \end{align*}\]
Der Flächeninhalt des Dreiecks \(ABC\) beträgt ca. 16,12 FE (Flächeneinheiten).
c) Koordinaten des Punktes \(D\), der das Dreieck \(ABC\) zu einer Raute ergänzt
Planskizze:
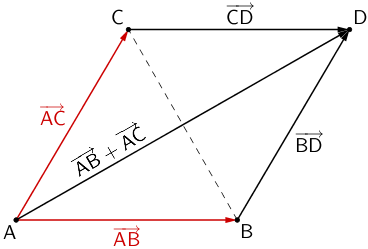
Der Punkt \(D\), der das gleichschenklige Dreieck \(ABC\) mit der Basis \([BC]\) zu einer Raute ergänzt, entsteht durch Verschiebung des Punktes \(B\) um den Vektor \(\overrightarrow{AC}\) bzw. durch Verschiebung des Punktes \(C\) um den Vektor \(\overrightarrow{AB}\).
Die Koordinaten des Punktes \(D\) lassen sich durch Vektoraddition wie folgt berechnen:
\(\overrightarrow{AB} = \begin{pmatrix} 2 \\ 4 \\ -4 \end{pmatrix}\), \(\overrightarrow{AC} = \begin{pmatrix} 4 \\ -2 \\ 4 \end{pmatrix}\) (vgl. Teilaufgabe a)
\[\begin{align*} \overrightarrow{D} &= \overrightarrow{B} + \overrightarrow{AC} \\[0.8em] &= \begin{pmatrix} 5 \\ 3 \\ 1 \end{pmatrix} + \begin{pmatrix} 4 \\ -2 \\ 4 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 9 \\ 1 \\ 5 \end{pmatrix} \end{align*}\]
\[\begin{align*} \overrightarrow{D} &= \overrightarrow{C} + \overrightarrow{AB} \\[0.8em] &= \begin{pmatrix} 7 \\ -3 \\ 9 \end{pmatrix} + \begin{pmatrix} 2 \\ 4 \\ -4 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 9 \\ 1 \\ 5 \end{pmatrix} \end{align*}\]
\[\begin{align*} \overrightarrow{D} &= \overrightarrow{A} + \overrightarrow{AB} + \overrightarrow{AC} \\[0.8em] &= \begin{pmatrix} 3 \\ -1 \\ 5 \end{pmatrix} + \begin{pmatrix} 2 \\ 4 \\ -4 \end{pmatrix} + \begin{pmatrix} 4 \\ -2 \\ 4 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 9 \\ 1 \\ 5 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad D(9|1|5)\]
d) Winkel \(\measuredangle{DBA} = \varphi\)
Planskizze:
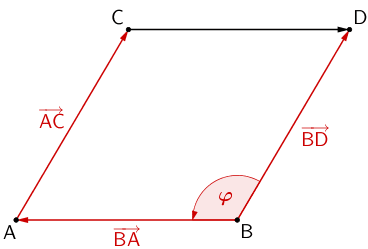
Winkel \(\measuredangle{DBA} = \varphi\) zwischen den Verbindungsvektoren \(\overrightarrow{BD} = \overrightarrow{AC}\) und \(\overrightarrow{BA} = -\overrightarrow{AB}\)
\(\overrightarrow{BD} = \overrightarrow{AC} = \begin{pmatrix} 4 \\ -2 \\ 4 \end{pmatrix}\) (vgl. Teilaufgabe a)
\(\overrightarrow{BA} = -\overrightarrow{AB} = -\begin{pmatrix} 2 \\ 4 \\ -4 \end{pmatrix} = \begin{pmatrix} -2 \\ -4 \\ 4 \end{pmatrix}\) (vgl. Teilaufgabe a)
Anwendung des Skalarprodukts:
Winkel zwischen zwei Vektoren (vgl. Merkhilfe)
\[\cos \varphi = \frac{\overrightarrow{a} \circ \overrightarrow{b}}{\vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert}\,; \quad \varphi \in [0;\pi]\]
\[\begin{align*} \cos{\varphi} &= \frac{\overrightarrow{BD} \circ \overrightarrow{BA}}{\vert \overrightarrow{BD} \vert \cdot \vert \overrightarrow{BA} \vert} & &| \; \overrightarrow{BD} = \overrightarrow{AC} \\[0.8em] &= \frac{\overrightarrow{AC} \circ \overrightarrow{BA}}{\vert \overrightarrow{AC} \vert \cdot \vert \overrightarrow{BA} \vert} \\[0.8em] &= \frac{\begin{pmatrix} 4 \\ -2 \\ 4 \end{pmatrix} \circ \begin{pmatrix} -2 \\ -4 \\ 4 \end{pmatrix}}{\left| \begin{pmatrix} 4 \\ -2 \\ 4 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} -2 \\ -4 \\ 4 \end{pmatrix} \right|} \\[0.8em] &= \frac{4 \cdot (-2) + (-2) \cdot (-4) + 4 \cdot 4}{\sqrt{4^{2} + (-2)^{2} + 4^{2}} \cdot \sqrt{(-2)^{2} + (-4)^{2} + 4^{2}}} \\[0.8em] &= \frac{16}{36} \\[0.8em] &= \frac{4}{9} & &| \; \text{TR:} \; \tan^{-1}(\dots) \\[3.82em] \varphi &\approx 63{,}61^{\circ} \end{align*}\]
e) Nachweis, dass die Strecke \([MS]\) des Mittelpunkts \(M\) der Grundkante \([BC]\) und der Pyramidenspitze \(S\) die Höhe der Pyramide \(ABCS\) ist
Planskizze:
![Pyramide ABCS mit Höhe [MS] Pyramide ABCS mit Höhe [MS]](/images/stories/Klausuren/Klausuren_Q11_2/Klausur_Q11_2-003/Klausur_Q11_2-003_A5e.png)
Das Vektorprodukt der Verbindungsvektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\) erzeugt einen Normalenvektor \(\overrightarrow{n}\), der senkrecht zu den Vektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\) ist, und damit senkrecht zur Grundfläche \(ABC\) der Pyramide \(ABCS\) ist.
Die Höhe einer Pyramide ist der Abstand der Spitze der Pyramide von der Grundfläche der Pyramide.
Die Strecke \([MS]\) ist die Höhe der Pyramide \(ABCS\), wenn die Strecke \([MS]\) senkrecht zur Grundfläche \(ABC\) ist. Dies ist dann der Fall, wenn der Verbindungsvektor \(\overrightarrow{MS}\) und der Normalenvektor \(\overrightarrow{n}\) parallel sind, das heißt, wenn sich der Vektor \(\overrightarrow{MS}\) durch ein skalares Vielfaches des Vektors \(\overrightarrow{n}\) (S-Muliplikation) darstellen lässt (oder umgekehrt). Es muss also gelten:
\[\overrightarrow{MS} = k \cdot \overrightarrow{n}; \; k \in \mathbb R\]
oder
\[\overrightarrow{n} = k \cdot \overrightarrow{MS}; \; k \in \mathbb R\]
Als Alternative überprüft man mithilfe des Skalarprodukts, ob die Vektoren \(\overrightarrow{MS}\) und \(\overrightarrow{AB}\) sowie \(\overrightarrow{MS}\) und \(\overrightarrow{AS}\) zueinander senkrecht sind. Das heißt, es muss gelten:
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{MS} \circ \overrightarrow{AB} = 0 \quad \Longleftrightarrow \quad \overrightarrow{MS} \perp \overrightarrow{AB}\]
und
\[\overrightarrow{MS} \circ \overrightarrow{AC} = 0 \quad \Longleftrightarrow \quad \overrightarrow{MS} \perp \overrightarrow{ABC}\]
1. Möglichkeit: \(\overrightarrow{MS} \parallel \overrightarrow{n}\) nachweisen
Das Ergebnis des Vektorprodukts \(\overrightarrow{AB} \times \overrightarrow{AC}\) kann der Lösung zu Teilaufgabe b entnommen werden.
\(\overrightarrow{n} = \overrightarrow{AB} \times \overrightarrow{AC} = \begin{pmatrix} 8 \\ -24 \\ -20 \end{pmatrix}\) (vgl. Teilaufgabe b)
Mittelpunkt \(M\) der Grundkante \([BC]\) der Pyramide \(ABCS\) berechnen:
\(B(5|3|1)\), \(C(7|-3|9)\)
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
\[\begin{align*}\overrightarrow{M} &= \frac{1}{2} \cdot ( \overrightarrow{B} + \overrightarrow{C} ) \\[0.8em] &= \frac{1}{2} \cdot \left[ \begin{pmatrix} 5 \\ 3 \\ 1 \end{pmatrix} + \begin{pmatrix} 7 \\ -3 \\ 9 \end{pmatrix} \right] \\[0.8em] &= \frac{1}{2} \cdot \begin{pmatrix} 12 \\ 0 \\ 10 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 6 \\ 0 \\ 5 \end{pmatrix} \end{align*}\]
Verbindungsvektor \(\overrightarrow{MS}\) berechnen:
\(S(4|6|10)\) (vgl. Angabe)
\[\overrightarrow{MS} = \overrightarrow{S} - \overrightarrow{M} = \begin{pmatrix} 4 \\ 6 \\ 10 \end{pmatrix} - \begin{pmatrix} 6 \\ 0 \\ 5 \end{pmatrix} = \begin{pmatrix} -2 \\ 6 \\ 5 \end{pmatrix}\]
Parallelität der Vektoren \(\overrightarrow{n}\) und \(\overrightarrow{MS}\) prüfen:
\[\begin{align*}\overrightarrow{MS} &= k \cdot \overrightarrow{n} & & (k \in \mathbb R)\\[0.8em] \begin{pmatrix} -2 \\ 6 \\ 5 \end{pmatrix} &= k \cdot \begin{pmatrix} 8 \\ -24 \\ -20 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad \left\{ \begin{align*} -2 &= k \cdot 8 \enspace \Longleftrightarrow \enspace k = -\frac{1}{4} \\[0.8em] 6 &= k \cdot (-24) \enspace \Longleftrightarrow \enspace k = -\frac{1}{4} \\[0.8em] 5 &= k \cdot (-20) \enspace \Longleftrightarrow \enspace k = -\frac{1}{4} \end{align*} \right.\]
\[\Longrightarrow \quad \overrightarrow{MS} = \left(-\frac{1}{4}\right) \cdot \overrightarrow{n} \quad \Longrightarrow \quad \overrightarrow{MS} \parallel \overrightarrow{n}\]
oder
\[\begin{align*}\overrightarrow{n} &= k \cdot \overrightarrow{MS} & & (k \in \mathbb R)\\[0.8em] \begin{pmatrix} 8 \\ -24 \\ -20 \end{pmatrix} &= k \cdot \begin{pmatrix} -2 \\ 6 \\ 5 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad \left\{ \begin{align*} 8 &= k \cdot (-2) \enspace \Longleftrightarrow \enspace k = -4 \\[0.8em] -24 &= k \cdot 6 \enspace \Longleftrightarrow \enspace k = -4 \\[0.8em] -20 &= k \cdot 5 \enspace \Longleftrightarrow \enspace k = -4 \end{align*} \right.\]
\[\Longrightarrow \quad \overrightarrow{n} = (-4) \cdot \overrightarrow{MS} \quad \Longrightarrow \quad \overrightarrow{MS} \parallel \overrightarrow{n}\]
Schlussfolgerung:
Die Strecke \([MS]\) des Mittelpunkts \(M\) der Grundkante \([BC]\) und der Pyramidenspitze \(S\) ist Höhe der Pyramide \(ABCS\).
2. Möglichkeit \(\overrightarrow{MS} \perp \overrightarrow{AB}\) und \(\overrightarrow{MS} \perp \overrightarrow{AC}\) nachweisen
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\(\overrightarrow{MS} = \begin{pmatrix} -2 \\ 6 \\ 5 \end{pmatrix}\) (vgl. 1. Möglichkeit)
\(\overrightarrow{AB} = \begin{pmatrix} 2 \\ 4 \\ -4 \end{pmatrix}; \; \overrightarrow{AC} = \begin{pmatrix} 4 \\ -2 \\ 4 \end{pmatrix}\) (vgl. Teilaufgabe a)
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*}\overrightarrow{MS} \circ \overrightarrow{AB} &= \begin{pmatrix} -2 \\ 6 \\ 5 \end{pmatrix} \circ \begin{pmatrix} 2 \\ 4 \\ -4 \end{pmatrix} \\[0.8em] &= (-2) \cdot 2 + 6 \cdot 4 + 5 \cdot (-4) \\[0.8em] &= -4 + 24 - 20 \\[0.8em] &= 0 \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{MS} \perp \overrightarrow{AB}\]
\[\begin{align*}\overrightarrow{MS} \circ \overrightarrow{AC} &= \begin{pmatrix} -2 \\ 6 \\ 5 \end{pmatrix} \circ \begin{pmatrix} 4 \\ -2 \\ 4 \end{pmatrix} \\[0.8em] &= (-2) \cdot 4 + 6 \cdot (-2) + 5 \cdot 4 \\[0.8em] &= -8 - 12 + 20 \\[0.8em] &= 0 \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{MS} \perp \overrightarrow{AC}\]
Schlussfolgerung:
Die Strecke \([MS]\) des Mittelpunkts \(M\) der Grundkante \([BC]\) und der Pyramidenspitze \(S\) ist Höhe der Pyramide \(ABCS\).
f) Maßzahl des Volumens der Pyramide \(ABCS\)
Die Maßzahl des Flächeninhalts der Grundfläche \(ABC\) der Pyramide \(ABCS\) ist aus Teilaufgabe b bereits bekannt.
Die Strecke \([MS]\) ist Höhe der Pyramide \(ABCS\).
Volumen einer Pyramide
\[V = \frac{1}{3} \cdot G \cdot h\]
\(G\): Flächeninhalt der Grundfläche der Pyramide
\(h\): Höhe der Pyramide
(vgl. Merkhilfe)
\(A_{ABC} = 2\sqrt{65}\) (vgl. Teilaufgabe b)
\(\overrightarrow{MS} = \begin{pmatrix} -2 \\ 6 \\ 5 \end{pmatrix}\) (vgl. Teilaufgabe e)
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} V_{ABCS} &= \frac{1}{3} \cdot A_{ABC} \cdot \vert \overrightarrow{MS} \vert \\[0.8em] &= \frac{1}{3} \cdot 2\sqrt{65} \cdot \left| \begin{pmatrix} -2 \\ 6 \\ 5 \end{pmatrix} \right| \\[0.8em] &= \frac{2}{3}\sqrt{65} \cdot \sqrt{(-2)^{2} + 6^{2} + 5^{2}} \\[0.8em] &= \frac{2}{3}\sqrt{65} \cdot \sqrt{65} \\[0.8em] &= \frac{2}{3} \cdot 65 \\[0.8em] &= 43\frac{1}{3} \end{align*}\]
Das Volumen der Pyramide \(ABCS\) beträgt \(43\frac{1}{3}\) VE (Volumeneinheiten).


