Spiegelt man die Punkte \(A\), \(B\) und \(C\) am Symmetriezentrum \(Z(3|3|3)\), so erhält man die Punkte \(A'\), \(B'\) bzw. \(C'\).
Beschreiben Sie die Lage der Ebene, in der die Punkte \(A\), \(B\) und \(Z\) liegen, im Koordinatensystem. Zeigen Sie, dass die Strecke \([CC']\) senkrecht auf dieser Ebene steht.
(3 BE)
Lösung zu Teilaufgabe b
Lage einer Ebene im Koordinatensystem, Lineare (Un-)Abhängigkeit von Vektoren
Lage der Ebene, in der die Punkte \(A\), \(B\) und \(Z\) liegen
\(A(6|3|3)\), \(B(3|6|3)\), \(Z(3|3|3)\)
Die Punkte \(A\), \(B\) und \(Z\) haben die gleiche \(x_{3}\)-Koordinate und sie liegen gemäß Aufgabenstellung in einer Ebene.
\[x_{3_{A}} = x_{3_{B}} = x_{3_{Z}} = 3\]
Folglich verläuft die Ebene, in der die Punkte \(A\), \(B\) und \(Z\) liegen, im Abstand 3 LE (Längeneinheiten) parallel zur \(x_{1}x_{2}\)-Ebene.
Eine Gleichung der Ebene ist beispielsweise:
\[x_{3} = 3\]
Anmerkung:
Würde die Aufgabenstellung nicht bereits festlegen, dass Die Punkte \(A\), \(B\) und \(Z\) in einer Ebene liegen, müsste überprüft werden, ob die Punkte ggf. auf einer Geraden liegen. Hierfür würde man beispielsweise mit den Punkten \(A\) und \(B\) eine Geradengleichung beschreiben und mit dem Punkte \(Z\) die Punktprobe durchführen.
Nachweis, dass die Strecke \([CC']\) senkrecht auf der Ebene steht, in der die Punkte \(A\), \(B\) und \(Z\) liegen
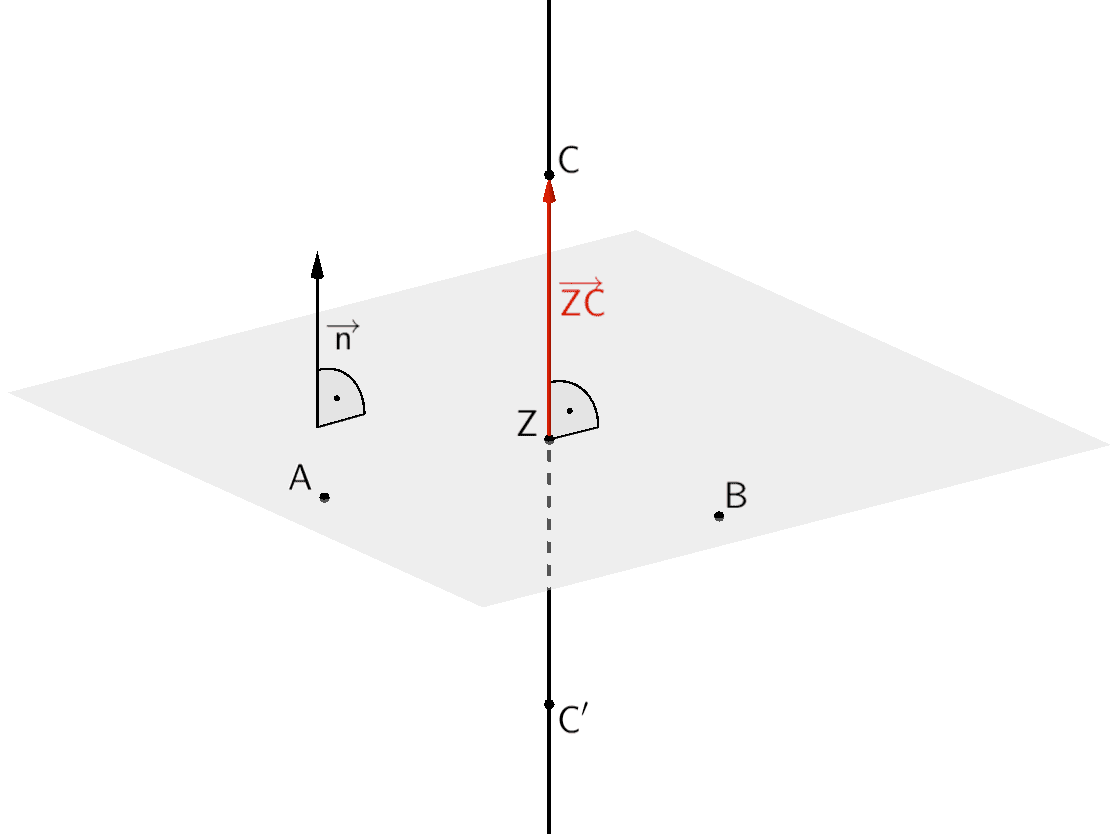
Der Punkt \(C'\) entsteht durch Spiegelung des Punktes \(C\) am Punkt \(Z\), was bedeutet, dass die Punkte \(C\), \(Z\) und \(C'\) auf einer Geraden liegen.
Folglich steht die Strecke \([CC']\) senkrecht auf der Ebene, in der die Punkte \(A\), \(B\) und \(Z\) liegen, wenn beispielsweise der Verbindungsvektor \(\overrightarrow{ZC}\) ein Normalenvektor dieser Ebene ist.
Da die Ebene, in der die Punkte \(A\), \(B\) und \(C\) liegen parallel zur \(x_{1}x_{2}\)-Ebene verläuft, ist \(\overrightarrow{n} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\) ein möglicher Normalenvektor dieser Ebene.
Der Verbindungsvektor \(\overrightarrow{ZC}\) ist ebenfalls ein möglicher Normalenvektor der Ebene, wenn die Vektoren \(\overrightarrow{n}\) und \(\overrightarrow{ZC}\) linear abhängig sind (parallel bzw. antiparallel zueinander sind).
Es muss also gelten::
Lineare (Un)Abhängigkeit von zwei Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind
linear abhängig, wenn
\(\overrightarrow{a} \parallel \overrightarrow{b}\) bzw. \(\overrightarrow{a} = k \cdot \overrightarrow{b}\) mit \(k \in \mathbb R\) gilt.
linear unabhängig, wenn
\(\overrightarrow{a} \nparallel \overrightarrow{b}\) bzw. \(\overrightarrow{a} \neq k \cdot \overrightarrow{b}\) mit \(k \in \mathbb R\) gilt.
Lineare (Un-)Abhängigkeit von drei Vektoren
Drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind
linear abhängig, wenn
sie in einer Ebene liegen bzw. wenn beispielsweise
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat.
linear unabhängig, wenn
sie den Raum \(\mathbb R^{3}\) aufspannen bzw. wenn beispielsweise
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat.
\[\overrightarrow{ZC} = k \cdot \overrightarrow{n}; \; k \in \mathbb R\]
Verbindungsvektor \(\overrightarrow{ZC}\) berechnen:
\(C(3|3|6)\), \(Z(3|3|3)\)
\[\overrightarrow{ZC} = \overrightarrow{C} - \overrightarrow{Z} = \begin{pmatrix} 3 \\ 3 \\ 6 \end{pmatrix} - \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix} = 3 \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\]
Lineare Abhängigkeit der Vektoren \(\overrightarrow{n}\) und \(\overrightarrow{ZC}\) prüfen:
Lineare (Un)Abhängigkeit von zwei Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind
linear abhängig, wenn
\(\overrightarrow{a} \parallel \overrightarrow{b}\) bzw. \(\overrightarrow{a} = k \cdot \overrightarrow{b}\) mit \(k \in \mathbb R\) gilt.
linear unabhängig, wenn
\(\overrightarrow{a} \nparallel \overrightarrow{b}\) bzw. \(\overrightarrow{a} \neq k \cdot \overrightarrow{b}\) mit \(k \in \mathbb R\) gilt.
Lineare (Un-)Abhängigkeit von drei Vektoren
Drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind
linear abhängig, wenn
sie in einer Ebene liegen bzw. wenn beispielsweise
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat.
linear unabhängig, wenn
sie den Raum \(\mathbb R^{3}\) aufspannen bzw. wenn beispielsweise
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat.
\(\overrightarrow{n} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\), \(\overrightarrow{ZC} = 3 \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\)
\[\Longrightarrow \quad \overrightarrow{ZC} = 3 \cdot \overrightarrow{n}\]
\(\Longrightarrow \quad\)Die Vektoren \(\overrightarrow{n}\) und \(\overrightarrow{ZC}\) sind linear abhängig.
Schlussfolgerung:
Der Verbindungsvektor \(\overrightarrow{ZC}\) ist ein Normalenvektor der Ebene, in der die Punkte \(A\), \(B\) und \(Z\) liegen. Folglich steht die Strecke \([CC']\) zwischen dem Punkt \(C\) und dem durch Spiegelung am Punkt \(Z\) entstandenen Bildpunkt \(C'\) senkrecht auf dieser Ebene.


