Beurteilen Sie, ob es einen Wert von \(k\) gibt, sodass \(G_{k}\) und \(G_{f}\) bezüglich der \(x\)-Achse symmetrisch zueinander liegen.
(2 BE)
Lösung zu Teilaufgabe 1i
\[h_{k}(x) = (1 - kx^{2}) \cdot e^{-x}; \;k \in \mathbb R, \; D_{h_{k}} = \mathbb R\]
\(f(x) = (1 - x^{2}) \cdot e^{-x}; \; D_{f} = \mathbb R\) (vgl. Aufgabe 1)
Es gibt keinen Wert von \(k\), sodass \(G_{k}\) und \(G_{f}\) bezüglich der \(x\)-Achse symmetrisch zueinander liegen.
Begründung
Würde es einen Wert von \(k\) geben, sodass \(G_{k}\) und \(G_{f}\) bezüglich der \(x\)-Achse symmetrisch zueinander liegen, müsste \(\textcolor{#0087c1}{h_{k}(x) = -f(x)}\) gelten.
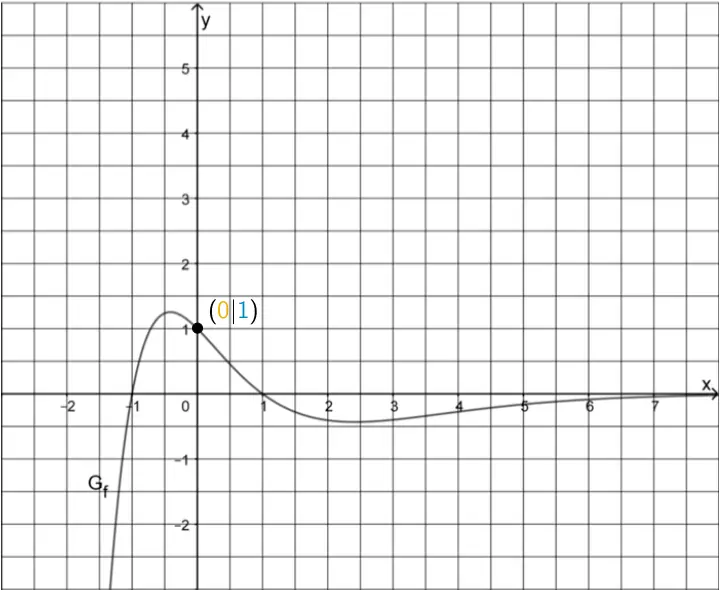
Um die Gültigkeit der Gleichung zu überprüfen, wählt man einen Punkt auf \(G_{f}\), beispielsweise den Schnittpunkt von \(G_{f}\) mit der \(y\)-Achse (vgl. Abbildung).
\[f(\textcolor{#e9b509}{0}) = (1 - \textcolor{#e9b509}{0}^{2}) \cdot \underbrace{e^{\textcolor{#e9b509}{0}}}_{1} = 1 \cdot 1 = \textcolor{#0087c1}{1}\]
Dann müsste \(h_{k}(\textcolor{#e9b509}{0}) = \textcolor{#0087c1}{-1}\) gelten.
\[h_{k}(\textcolor{#e9b509}{0}) = (1 - k \cdot \textcolor{#e9b509}{0}^{2}) \cdot \underbrace{e^{\textcolor{#e9b509}{0}}}_{1} = 1\]
Da für alle \(k \in \mathbb R\) gilt \(h_{k}(\textcolor{#e9b509}{0}) = 1 \neq \textcolor{#0087c1}{-1}\), gibt es keinen Wert von \(k\), sodass \(G_{k}\) und \(G_{f}\) bezüglich der \(x\)-Achse symmetrisch zueinander liegen.


