Abiturlösungen Mathematik Bayern Beispiel-Abiturprüfung 2026 Prüfungsteil A Aufgabengruppe 2 (Wahlteil)
- Details
- Kategorie: Aufgabengruppe 2 (Wahlteil)
Gegeben sind die in \(\mathbb R\) definierten Funktionen \(f\) und \(g\). Der Graph von \(f\) ist symmetrisch bezüglich der \(y\)-Achse, der Graph von \(g\) ist symmetrisch bezüglich des Koordinatenursprungs. Beide Graphen haben einen Hochpunkt im Punkt \((2|1)\).
- Geben Sie für die Graphen von \(f\) und \(g\) jeweils die Koordinaten und die Art eines weiteren Extrempunkts an.
(2 BE) - Untersuchen Sie die in \(\mathbb R\) definierte Funktion \(h\) mit \(h(x) = f(x) \cdot \left( g(x) \right)^3\) im Hinblick auf eine mögliche Symmetrie ihres Graphen.
(3 BE)
- Details
- Kategorie: Aufgabengruppe 2 (Wahlteil)
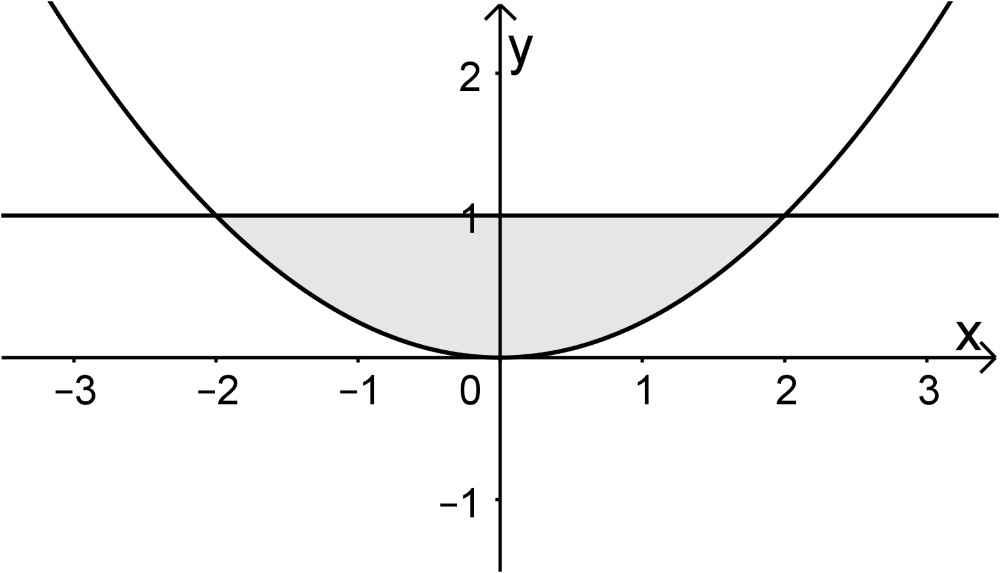
Der Graph der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto \frac{1}{4}x^2\) und die Gerade mit der Gleichung \(y = 1\) schließen ein Flächenstück ein (vgl. Abbildung). Durch Rotation diese Flächenstücks um die \(y\)-Achse wird ein Körper erzeugt. Bestimmen Sie das Volumen dieses Körpers.
(5 BE)
- Details
- Kategorie: Aufgabengruppe 2 (Wahlteil)
Bei einem Spiel werfen zwei Spieler abwechselnd jeweils drei Würfel. Das Spiel endet, wenn ein Spieler die Augensumme 18 erzielt oder die Augensumme des vorausgegangenen Wurfs des anderen Spielers nicht übertrifft.
Beim ersten Wurf des Spiels erzielt ein Spieler die Augensumme 15.
Berechnen Sie die Wahrscheinlichkeit dafür, dass dieser Spieler die Würfel im selben Spiel noch einmal wirft. Erläutern Sie Ihr Vorgehen.
(5 BE)
- Details
- Kategorie: Aufgabengruppe 2 (Wahlteil)
Eine Gärtnerei, die Tulpen in den Farben Gelb, Orange und Rot züchtet, stellt Sträuße mit jeweils 15 Tulpen zusammen.
- Einer der Sträuße soll Tulpen in zwei verschiedenen Farben enthalten. Die Anzahl der Möglichkeiten, diesen Strauß zusammenzustellen, kann mit dem Term \(\displaystyle \binom{3}{2} \cdot 14\) berechnet werden. Beschreiben Sie für jeden der beiden Faktoren die Bedeutung im Sachzusammenhang.
- In einem der Sträuße sollen zu jeder der drei Farben mindestens vier und höchstens sechs Tulpen enthalten sein. Bestimmen Sie die Anzahl der Möglichkeiten, diesen Strauß zusammenzustellen.
- Details
- Kategorie: Aufgabengruppe 2 (Wahlteil)
Gegeben sind die Punkte \(A(0|0|0)\), \(B(3|4|1)\), \(C(1|7|3)\), \(D(-2|3|2)\).
- Weisen Sie nach, dass das Viereck \(ABCD\) ein Parallelogramm ist.
(1 BE) - Der Punkt \(T\) liegt auf der Strecke \(\overline{AC}\). Das Dreieck \(ABT\) hat bei \(B\) einen rechten Winkel. Ermitteln Sie das Verhältnis der Länge der Strecke \(\overline{AT}\) zur Länge der Strecke \(\overline{CT}\).
(4 BE)
- Details
- Kategorie: Aufgabengruppe 2 (Wahlteil)
Die Punkte \(P\) und \(Q\) liegen in der Ebene \(E \colon 5x_1 - 4x_2 + 3x_3 - 6 =-3 0\) und haben voneinander den Abstand 10. Ermitteln Sie mögliche Koordinaten von \(P\) und \(Q\).
(5 BE)


