Man liest gelegentlich, eine nach rechts geneigte Handschrift weise darauf hin, dass die zugehörige Person aufgeschlossen ist. In einem Unternehmen mit 50 Angestellten gelten 35 als aufgeschlossen. 40 % der als aufgeschlossen geltenden Angestellten haben eine Handschrift, die nicht nach rechts geneigt ist. Sechs Angestellte, die nicht als aufgeschlossen gelten, haben eine nach rechts geneigte Handschrift.
Betrachtet werden folgende Ereignisse:
\(A\,\colon\;\)„Ein zufällig ausgewählter Angestellter gilt als aufgeschlossen."
\(R\,\colon \;\)„Ein zufällig ausgewählter Angestellter hat eine nach rechts geneigte Handschrift."
Beschreiben Sie das Ereignis \(\overline{A \cap R}\) im Sachzusammenhang.
(2 BE)
Lösung zu Teilaufgabe a
Veranschaulichung des Ereignisses \(\overline{A \cap R}\) mit Venn-Diagramm
Gesetze von de Morgan
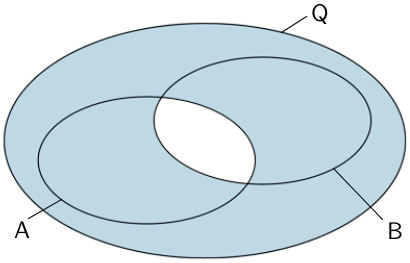
Weder Ereignis \(A\) noch Ereignis \(B\); Keines der beiden Ereignisse
\[\overline{A} \cap \overline{B} = \overline{A \cup B}\]
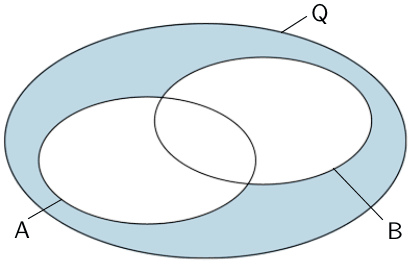
Nicht beide Ereignisse \(A\) und \(B\) zugleich; Höchstens eines der beiden Ereignisse
\[\overline{A \cap B} = \overline{A} \cup \overline{B}\]
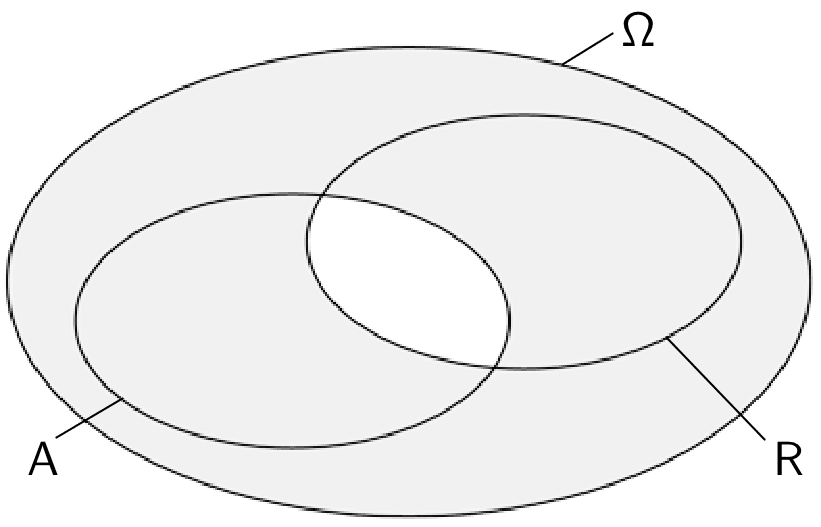
Venn-Diagramm (Mengendiagramm) für das Ereignis \(\,\overline{A \cap R} = \overline{A} \cup \overline{R}\)
Wortlaut: „Nicht beide Ereignisse \(A\) und \(R\) gleichzeitig" oder „Höchstens eines der beiden Ereignisse \(A\) und \(R\) tritt ein".
Ereignis \(\overline{A \cap R}\) im Sachzusammenhang
„Ein zufällig ausgewählter Angestellter gilt nicht als aufgeschlossen oder hat keine nach rechts geneigte Handschrift."
Das mathematische „oder" der Vereinigungsmenge \(\overline{A} \cup \overline{R}\) bedeutet:
Ein zufällig ausgewählter Angestellter
- gilt nicht als aufgeschlossen oder
- hat keine nach rechts geneigte Handschrift oder
- gilt nicht als aufgeschlossen und hat keine nach rechts geneigte Handschrift.


